pooneilの脳科学論文コメント

■ Natureで久しぶりにsingle-unit study

「神経：眼窩前頭皮質ニューロンは経済的価値を符号化する」
"Neurons in the orbitofrontal cortex encode economic value" Camillo Padoa-Schioppa and John A. Assad
おおひさしぶりにNatureに! と思ったらなんかneuroeconomics追いかけましたよ、みたいな雰囲気。しかもぱっと見orbitofrontalからの記録だし、TREMBLAY AND SCHULTZのNature '99 ("Relative reward preference in primate orbitofrontal cortex")との違いがわからない。
読んでないけど。

■ Daeyeol Leeからsubjective valueへ

ryasudaさんのNature NeuroscienceがAOPに載った、というのを聞きつけて見に行ったついでで、Daeyeol Leeの論文がAOPに掲載されているのを発見。
"Activity in prefrontal cortex during dynamic selection of action sequences"
んで、まだ読んでないんだけれど、abstの最後の"subjective knowledge of the correct action sequence"を見て、言いたいことを思い出したので一つ。
なんつうか、時間的にlocalなところのreward historyしか使えない状況とか、、もしくはゲーム理論的なシチュエーションでプレーヤー自身が限られた知識(相手側がどう行動するかはうかがい知れない、とか)しか持っていない状況とか、そういうものに対して"subjective"という言葉を使うことがあります。
以前わたしがDorris and Glimcherで問題にしたのは、subjective valueと言っているわりにはexpected utilityではなくてexpected valueを使っているという点でした。しかし、上記の視点が限定されている、という意味でsubjectiveを使ってしまえば、実験者が設定したreward(trial block中で一定な、いわゆるglobalな値)から計算されるvalueではなくて、短い限られたtrialでのreward historyから被験者が推定したrewardから計算されるvalueをsubjective rewardと言ってしまうことも可能です。言い抜けだと思いますけど。
んで、Sugrue and NewsomeのNature Review Neuroscienceでのlocalかglobalか、という議論のところではたしかそういう表現をしていたところがあったような。ということが頭に引っかかっていたんだけれど、思い出したのでメモ。
う、タイトルというかカテゴリ名が長い。このへんまで来ると、カテゴリ名よりはタグ的に扱ったほうが良いんだろうなあ。

■ Nature Reviews Neuroscience 5月号 Sugrue論文続報

"CHOOSING THE GREATER OF TWO GOODS: NEURAL CURRENCIES FOR VALUATION AND DECISION MAKING." Leo P. Sugrue, Greg S. Corrado and William T. Newsome

Nature Reviews Neuroscienceに[Newsome '04 Science 選択行動]スレッドで採りあげたScience論文の続報(というかDorris論文との関連づけのディスカッション)が載っています。 まだちらっとしか見てませんが、以前問題としていたSugrue論文とDorris論文との関連について議論していたところがもろに取りざたされているようです。私としてはLocal time scaleとglobal time scaleとを明確に分けて議論することでSugrue論文とDorris論文の間に一見あるように見える矛盾を解消する、というのは納得のいく感じがあります。

20050117のコメント欄にuchidaさんからコメント書き込みあります(レスポンス遅れてすみません)。最新のエントリでないとコメントが目立たないのでここに採録しておきます。uchidaさんwrote:

　ご無沙汰しています。新しい総説、Sugrue et al (Nature Review Neurosci., 2005)、ご覧になられたことと思います。知りたかった解析（Sugrue et al., 2004 のデータをDorris et al, 2004 の方法で解析すること）が出ていますね (Figure 7)!!! 少なくともこれらふたつのニューロンはとても似た振る舞いをしていることが分かります。Population data をきっちりみたいところですが、Newsome グループがこのニューロンを出してきたということは、お互いほぼ同じようなニューロンを見ていると考えるのが自然のような気がします。驚くべき一致ですね!!! 従って、今後はどのように解釈するかということが主眼になるかとおもいますが、そのあたりは今後のGlimcher の反論も含めてじっくりみていく価値がありそうですね。
　この総説で強調されている、local な解析・モデルが｢メカニズム｣により近いはずだから、グローバルな解析より重要だという主張は一理あります。しかし、図7は、expected value が task 中、グローバルに変動しない場合（以前私の書き込みで示したように matching task ではグローバルには expected value が変動しない）、ニューロンの発火頻度も大きく変動しないということをはっきり示しています。Newsome らに決定的に欠けているのは、Dorris et al. (2004) で行われた報酬量を変化させる実験、つまりexpected value をふる実験で、これをしない限り、localな細かな変動をあたかもすべてのように語るのは大きな間違いという気がします。大きな方手落ちです。 Dorris らが示したように、報酬量を変動させたときには local fluctuation よりもずっと大きな変動を起こすことが考えられるからです。そういうことから考えると、この総説の一方的な攻撃に反して、Glimcher らが結局正しいということになるのではないかという予感がします。この総説が、著者の意図に反して大きな欠陥をさらけ出してしまうのではないか。。。
　はたからみているだけでなく、自分もなにか面白いことを始めなければ。。。

けっきょくのところ、local valueとgloval valueとがどう関係づけられるか（行動的およびニューロンメカニズム的に）というあたりの解明が進めることがこの戦いに決着を付けるのではないかと思います。SFNでの報告を見る限り、Glimcherたちはbasal gangliaのニューロン記録も進めているようなのですが、そういう意味ではそれは正しい道のように思えます。

■ Businessweek on 神経経済学(neuroeconomics)

んでひさしぶりに神経経済学でググってみたら、Businessweekで採りあげられた("Why Logic Often Takes A Backseat.")ということもあって、いくつかの有名blogでも「神経経済学」という語が言及されていることを発見しました。

• Joi Ito's Web 20050411
• On Off and Beyond 20050406

せっかくなので、Businessweekで採りあげられている話の元ネタをリストアップしてみましょう：

• はじめに出てくる、アンフェアに扱われたときにanterior insula(前島)が活動する、というやつはJonathan D. CohenのScience '03 "The Neural Basis of Economic Decision-Making in the Ultimatum Game"
• Colin F. Camerer, an economist at Caltechは上記論文へのコメントをScience '03に書いてます。PSYCHOLOGY AND ECONOMICS: Enhanced: Strategizing in the Brain
• Harvard University economist David I. LaibsonはJonathan D. CohenのScience '04 "Separate Neural Systems Value Immediate and Delayed Monetary Rewards."の著者のうちの一人です。"time inconsistency"とか"quasi-hyperbolic discounting"とか、前回のエントリと関連するキーワードが並んでます。
• Antonio R. Damasioが言う、emotionがdecision makingに及ぼす重要な役割はJNS '99 "Different Contributions of the Human Amygdala and Ventromedial Prefrontal Cortex to Decision-Making."

■ Current Bliology 4/12 神経経済学

"Single Units in the Pigeon Brain Integrate Reward Amount and Time-to-Reward in an Impulsive Choice Task."
神経経済学(Neuroeconomics)関連。Pigeonのprefrontal cortexアナログので電気生理。しかも"rewards' subjective values"ときました。すぐ手に入る小さい報酬と待たなければならないけど大きい報酬、どちらを選ぶかという課題。全体として得られる報酬量を最大化するよりは、時間遅れをどのくらい評価するかという重み付け(discounting function)によって選択が影響を受ける、という意味で"subjective value"なわけですな。
この論文へのコメンタリはこちら："Neuroeconomics: The Shadow of the Future."
課題としてはこんな感じ：被験者はlarge rewardかsmall rewardかのどちらかの選択をさせられる。その選択をしてからじっさいに報酬が与えられるまでの待ち時間はsmall rewardでは一定(1.5sec)、large rewardではblockごとに決まっていて、blockごとにだんだん長くなってくる(1.5sec-48sec)。だから、はじめの方のblockでは被験者はlarge rewardばかりを選ぶのだけれど、あとの方のblockになるとlarge rewardを選んだ場合に待ち時間が長いことがわかっているのでどっかでsmall rewardを選ぶように方針転換するわけです。
ニューロンのデータの結果：この待ち時間のあいだのニューロン活動を記録すると、はじめの方のblock(Fig.3Aのblock-3、余裕でlarge rewardを選択)では待ち時間のあいだのニューロン活動が大きいのに対して、つづくblock(Fig.3Aのblock-1、だんだんlarge rewardを選んでてよいものかどうか迷いのある状態)ではニューロン活動が小さくなってくる。さらにある時点でlarge rewardを選ぶのをやめてsmall rewardを選ぶことにするとニューロンの活動はもうblock(Fig.3Aのblock1-3)によって変化がない。じっさい、small rewardを選ぶと1.5sec後に必ず報酬が得られるわけだから。おもしろいのは、block1-3の時の活動の方がsmall rewardを選択しているにもかかわらずblock-1のとき(large rewardを選択)より活動が大きいのですな。Block-1で被験者はなんか損してるなと思いつつlarge rewardを選んでいる、という感じがしているに違いない。そういう感情移入をしてみると、なんかsubjectiveなvalueをコードしてる感じがしてきます。
話を戻して、結果のまとめ：というわけでこのニューロンはたんにlarge rewardを選んだかsmall rewardを選んだかということだけでなく、large rewardを選んでからどのくらい待てばrewardが得られるか(time to reward)、という情報も持っている、というのが著者らの主張です。この解釈が唯一なものかどうかはわかりません。とくにcriticalな差がblock間の差でランダマイズされていない、しかもlarge rewardからsmall rewardへ転換、という順番が固定されているがゆえに何らかの系統的な変化が起こっていてもおかしくないわけだし。
"Time to reward"に関連するものという意味ではこのあいだのShadlenのNature Neuroscience '05 "A representation of the hazard rate of elapsed time in macaque area LIP."あたりとも結びつけて考えてみたい感じがします。じっさい、Fig.3Aのblock -3や-2で現れるピークなんかはなんか意味ありげに見えるし。
将来の利益を得ようとせずに目先の欲望に惑わされてしまう"Impulsive Choice"という文脈で、関連する課題がCardinal et al. Science '01 "Impulsive choice induced in rats by lesions of the nucleus accumbens core."で使われていることを20040704のmmmmさんがコメント欄で紹介していました。また、human fMRIではJonathan D. CohenのScience '04 "Separate Neural Systems Value Immediate and Delayed Monetary Rewards."や銅谷さんのNature Neuroscience '04 "Prediction of immediate and future rewards differentially recruits cortico-basal ganglia loops."がimmediate rewardとfuture rewardという問題を扱っています。
Discounting functionがhyperbolicかexponentialか、という話題については20040704のmmrlさんのコメントで言及されてましたね。あの時点で私がぜんぜん論点を理解してなかったことがいまさら丸わかりなわけですが。なお、今回の論文ではpopulationとしてはhyperbolicの方がニューロンのデータをよく説明できる、ということのようです（Fig.4Cみるとあんまり差がないけど）。
なお、以上のコメントは論文の図だけ読んで書いていることを白状しときます。

■ Dorris and Glimcher (2004)とSugrue et al(2004)(mmrlさんより)

mmrlさんが1/4コメント欄で言及していた計算をしてくださったものが届きました。許可をいただいたので以下に掲載します。mmrlさん、いつもどうもありがとうございます。ここから：

---

ちょっと計算してみましたのでご報告。

やったことは、matchingとmaximizing(強化学習、Optimization)で得られる解が違うのかどうかをSugrueらの離散時間型のVI-VIスケジュールで確認しました。

結論を先に言うとVI-VIの場合、

1. maximizingの解はmatchingの解に一致する
2. このときの各expected value for choiceは等しい

の２点です。

maximizationでは違う解が得られるのではないかと期待していたのですが、一致してかつuchidaさんが数行で計算した結果をいろいろいじくって確認しただけとなりました。また、簡単のため選択変更後遅延(change over delay, COD)はこの計算では用いていません。

7月1日に計算したように、n 回あるchoice Aを選択しなければ、そこに報酬が存在する確率は、

と表されます。ここで、は１回に報酬が降ってくる確率。

今、確率的に行動選択するとして、A を選択する確率とすると、まったくランダムに選択したとするとそのinter choice interval の分布は

このとき、expected value for choice A, はchoice probabiltiy の関数になって、

となります。同様に

これは、を下げれば下げるほどを上げることになります。

一方、income の方は

となりますからを下げれば0に漸近、1に近づければに漸近します。

maximization では、ある選択確率 のときの単位時間当たりの総報酬を最大化するわけですから、

が最大になるように、を見つければよいので微分して0に持っていけばよい。

ここで、となることに注意すると

において から によって最適解が与えられる。 すなわち均衡解というわけです。

さて、これで得られる解が

fractional income

のどのような関数になっているかというと とから

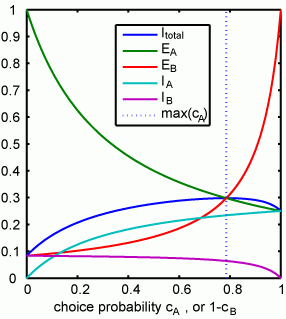
すなわちAのfractional incomeはAのchoice probability に一致する。つまりmatchingというわけです。あーつまんない計算だった。

休み２日掛けて考えたのに結局ＶＩＶＩはmatching とmaximizingが一致するように巧妙に仕組まれたタスクということだけがわかりました。

これって実はBaum 1981, Heyman 1979, Staddon Motheral 1978に書かれていたいりして...、調べてから計算しよう。ああ、無駄してしまった。

7月1日に書いたことも実はmomentary maximization theory (瞬時最大化理論)と呼ばれるものと同一だったりすることを[メイザーの学習と行動」を読み返して気づいてみたり...。無駄ばっかり。

---

ここまでです。編集過程で間違いが混入していたらお知らせください。

いやいや､無駄ではないですよ。手を動かした人がいちばん問題を理解した人になると思いますし。

メールにも書きましたが､generalizedでないMatching lawが成り立つためにはchange over delayの導入とVI-VI concurrentであることとが必須であるという理解だったのですが、今回の計算からするとchange over delay自体はalternating choiceのstrategyを排除するためだけに必要で、そんなにエッセンシャルなものではないのかもしれませんね。

しかしここまでくるとchange over delayとtauを組み込んだときにmaximizationとmatchingとの解がどのくらいずれるかということも検証できてしまいそうですね。それについては将来の著者たちの研究を待つか､ガッツのある方の参入を期待するということで､まずはmmrlさん、ありがとうございました。

■ Dorris and Glimcher (2004)とSugrue et al(2004)

どうも遅くなりました。頭がなかなか戻らないのでとりあえず思い出せるかぎりでレスポンスします。

まずはuchidaさん､すばらしいコメントをどうもありがとうございます。こういうサイトをやっていてよかったと思うのはまさにこういうときです。サイトなしにはなかなかお知りあいになる機会のなかった方とお知りあいになることができて､自分ひとりではできなかった議論を日本中､世界中をまたいですることができる､こういうことを積み重ねてネットワークを広げていくことができたらすばらしいと思ってます。

……global な相関（あるいは変動しないこと）と、local な相関、つまり、論文中の３つの仮説のうちのふたつ……の関係をもう少しきっちり詰めることが、この論文で示されたデータを読み解き、Sugrue et al (2004) との関係をはっきりさせる上で重要だと思います。

では、Sugrue et al論文の方はどうかというと､以前(7/5) Sugrue et al論文がglobalなmatchingとlocalなmatchingとを明示的に比較するようになっていない、ということを指摘しました。つまり、Sugrue et al論文ではLIPのactivityでglobal matchingを説明することはできなかったので、時間的にlocalなところのことしか考えていないのです。彼らはglobalにexpected value of choicesが等しいということが成り立つところでの現象を見ていないのかもしれません。

一方で、Dorris and Glimcher論文では基本的にglobalなtime scaleでナッシュ均衡が起こっていると見なしたうえで)、expected value of choicesとresponse probabilityとを分離しようとした試みである、と言えます（localなtime scaleではナッシュ均衡は成り立っていません）。

そうなると両者のあいだで見られるような矛盾はたんに見ようとしているタイムスケールの違いで解決するのかもしれません。この点でryasudaさんのご指摘にあったように、

……Nao(Uchida-san)'s statement (R_A/N_A = R_B/N_B) is not generally true for the leaky-integrator model

matching taskにおいてlocalなtime scaleではR_A/N_A = R_B/N_Bが必ずしも成り立たない､ということは大きな意味を持っていると言えます。つまりryasudaさんの予測にあるように､Sugrue et alとDorris and Glimcherのどちらにおいてもexpected value for choicesが等しいと言えるのはglobalなtime scaleでの話であって､localなtime scaleではどちらの論文でも成り立っていないのです。それで、Sugrue et alはlocalなところに話を終始させたし､Dorris and Glimcherはじゅうぶん均衡に達していないデータを使ってたのでchoice probabilityもexpected valueも変動してしまっている、というわけです。

では、Sugrue et al の model と強化学習のモデルの違いの本質はどこにあるのですか？

そもそもmatching law自体は経験的な法則であって､matching lawがどういう原理によって成立しているのかということ自体が論争になっていることについて以前触れました(6/30など)。いくつかの説の中で､Optimization (= reinforcement learning)をした結果マッチングが起こっている､という説に関しては、メイザー自身がoptimizationよりもマッチングのほうが説明力があるというデータを呈示しているらしいです(6/30)。

また、uchidaさんのご指摘に関連するところでは､Melioration theory(逐次的改良理論)という説をメイザーは押しています。Melioration theoryとは、二つのchoiceのあいだで選択数/強化が等しくなるように選択をした結果､マッチングが成り立つ､というものです(手元に「メイザーの学習と行動」がないのでhttp://www.montana.edu/wwwpy/Faculty/Lynch/MazurChap14.htmを参考に)。まさにこのリンクにも書いてありますが､逆数を取ればpayoff rate (= reinforcement/no of choices = expected value for choices)で、uchidaさんが見出したものと同じものとなります。つまり、Melioration theoryが正しいとすると､二つの選択肢のexpected valueが等しくなるように選択率を調整することによってその結果､マッチングが成り立つ､ということになります。これは二つの選択肢に関してindifferentになるように選択する､というまさにゲーム理論的な行動の現れと取ることができます。じっさい､以前リンクした"高橋雅治(1997) 選択行動の研究における最近の展開：比較意思決定研究にむけて"でも最後のほうに選択理論とプロスペクト理論とを関連付ける（将来的に融合される）という展望について語られています。

というあたりまで見渡してみると､uchidaさんのご指摘はまさにいまホットな話題である部分に直接関わることであり､今後の意思決定の研究がどういう道具立てで行くべきか、つまりゲーム理論/強化学習/選択理論をどう統一的なフレームワークで扱うか､ということに関する本質的な議論なのではないかと思います。

■ Dorris and Glimcher (2004)とSugrue et al(2004)に関して(by uchidaさん)

uchidaさん@Cold Spring Harbor laboratoryからDorris and Glimcher (2004)とSugrue et al (2004)とに関するコメントをいただきました。許可をいただいたので以下に掲載します。今日はuchidaさんによるゲストブログということで、＜blockquote＞に入れないで地の文に入れます。なお、uchidaさんはリンク先をご覧になればおわかりのようにratのolfactory系によるdecisionの研究で成果を出しておられる方です。

Dorris and Glimcher論文とSugrue et al論文とを比較して､Dorris and Glimcherではchoice probabilityをexpected valueからdissociateできているのではないか､というご指摘です。これはDorris and Glimcher論文のSugrue et al論文に対するneuesを評価するにあたって重要なご指摘であるかと思います。私ももう少し考えてみるつもりですが､皆様のコメントがいただけたらと思います。ここから：

---

最近見付け、読ませて頂いています。こういうサイトで論文を深く掘り下げることができれば大変ためになりますね。ますますの発展をお祈りしています。以下は大部分すでに議論されていたことの繰り返しになりますが、私なりの意見を述べさせていただきたいと思います。

[Neuroeconomics]

Dorris and Glimcher (2004) および、Sugrue et al (2004) は、Barraclough et al. (2004) と共に、新しい研究パラダイムを切り開きつつあるという点で、大変興味深く見ています。ただ、３論文とも行動の解析は非常におもしろいのですが、実際に神経生理の研究という視点で見た場合、どれだけ新しいパラダイムがいかせているか、という点をもう少し考えてみる必要があるのではないかと思っています。３つの論文を比べると、その点においては、Dorris and Glimcher (2004) がもっともうまく行動パラダイムをデザインしているのではないかという印象を持ちました。

[Local fractional income and choice probability]

Sugrue et al (2004)は、matching behavior が、”local” なreward history (”local fractional income”) で説明できるということを提案したという点が非常におもしろいです。このモデルは、非常にparsimonious で、しかも従来のglobal matching に比べてmechanistic に非常にstraightforward で、その点が優れていると思います。何と言ってもglobal なvariable interval schedule を知らなくても、matching が実現できるというわけですから。

一方、Sugrue et al (2004)の限界のひとつは、”response probability”*1と、”local fractional income” が非常に相関していて切り離せないために、結局、LIP neuron がどちらをコードしているのか（このふたつのどちらかと仮定して）を決定できない点にあるのではないでしょうか。以前、Newsomeのトークを聞いていたとき、この点を質問されて、local fractional income がresponse probability をコントロールしているので。。。deep question だというようなことを言って逃れていました。

[Desirability or expected value of choice]

一方、Dorris and Glimcher (2004)がみているのは、desirability of actionあるいはexpected value of choiceで、後に述べますように、これは fractional income とは少し異なる概念です。すでにこのサイトで議論されているように、subjective vs. objective あるいは、expected utility vs. expected valueの関係、違いは、この論文の議論の弱点であると思います。しかしここでは、その点を差っぴいて、LIP neuron のactivity が結局何と相関しているのかを読む点に力点を置きたいと思います。そのために議論の厳密さが失われることも考えられますが、その点はご容赦ください。Expected value of choice と、local fractional incomeの違いは Daw and Dayan (2004) でも軽く触れられていますが、以下でもう少し考えてみたいと思います。

Dorris and Glimcher (2004)では、Nash equilibrium に達していると仮定するとふたつのchoice のexpected value （本来なら expected utility）が等価になることを利用して、expected value と、response probability を切り離すことを実験のデザインの肝としました。そして、LIP neuron は、inspection game中、response probability が変化しても（Nash equilibrium と仮定して）relative expected value of choice が変化しないときには発火頻度が変化しないが、instructed saccade trials で報酬量を変化させてrelative expected value of choiceを変化させたときにはそれに伴って発火頻度が変動することを示しました。

さて、ふたつの論文は一見似た結論に達しているように見えるかもしれませんが、全く正反対の結論に達していると言ってもいいのではないでしょうか？これは、matching task で、expected value of choice がどうなっているかを考えると明らかになります（式で考えなくても明らかだと思いますが。。。）。

[Expected value in matching task]

サルが、あるブロックでターゲットA, B (red or green)を選んだ回数を、とします。また、そのブロックで報酬を得た回数をそれぞれ、とします。

すると、expected value for choice A および B は、

、

となります。（expected value for choiceは、一回のchioce あたりに得られる報酬量の期待値で、Daw and Dayan, 2004 で return と呼ばれているものに相当すると思います。）

ところで、このブロックで global matching が起こっていたとすると、、をAおよびBを選んだ確率 (response probability) とすると、

、

が成り立つわけですが、

から、

つまり、choice A、choice B に対するexpected value for choiceが等価であることを示しています。つまり、matching task においても、relative expected value for choice がinspection game と同様の振る舞いをしている可能性が考えられます。このことは、おそらくlocal な計算をした場合でも成り立っているのではないかと想像しています。

このことからmatching task では（fig D, in Daw and Dayan, 2004にあるように）variable interval schedule を変化させても、relative expected value for choice (relative return) は変化しないと考えられます(もちろんlocal なfluctuation はあるち思われますが。。。)。従って、Sugrue et al (2004)は、積極的に、｢LIP neuron は、relative expected value for choice をコードしているのではない｣という結論に達する可能性も考えられます。逆に、Dorris and Glimcher (2004)は、積極的にresponse probability と相関していない点が彼らにとって重要な点です (Fig. 7)。Local fractional income とニューロンの活動が相関していないことは直接は示していませんが。。。

[trial-by-trial variability of desirability of choice]

Dorris and Glimcher (2004) では、その後、LIP neuron の細かな trial-by-trial variability が、”dynamic (local) estimate of relative subjective desirability” と相関しているかを検証しています。どちらの選択をするべきかその時々のdesirability は、opponent を演じていた computerが用いていたreinforcement learning algorithm を使って推定されています。その結果、LIP neuron の発火頻度が relative desirability と相関している、と主張しています(Fig. 9)。

では、この “desirability” とはそもそも何でしょうか？ desirability は、少なくともcomputer opponent では、computer の選択をバイアスさせる値ですので、当然、desirability とresponse probability は相関しているはずです。。。従って、上で検討した response probability と LIP neuron の発火頻度を切り離したという議論がどこまで成り立つのか、あるいは、どういう形で成り立つのか、という点に疑問が残ります。そういう眼でもう一度 Fig. 6A を見てみると、確かに、各ブロックごとの平均発火頻度はほぼ変動していないように見えますが、各ブロック内でのlocal な変動に注目してみると若干response probability と相関して変動しているように見えるところもあります。単に想像に過ぎませんが、｢response probability から各ブロックでの平均 response probability を差し引いたもの｣を考えると、LIP neuron の発火頻度と相関しているのかも知れません(単なる読み過ぎの可能性も大ですが。。。)。

いずれにしても、global な相関（あるいは変動しないこと）と、local な相関、つまり、論文中の３つの仮説のうちのふたつ、”whenever the animals are at a mixed strategy equilibrium during the inspection game, the average firing rates of LIP neurons should be fixed ”と、”On a trial-by-trial basis, however, the mixed strategy equilibrium is presumed to be maintained by small fluctuations in the subjective desirability of each option around this fixed level caused by dynamic interactions with the opponent” の関係をもう少しきっちり詰めることが、この論文で示されたデータを読み解き、Sugrue et al (2004) との関係をはっきりさせる上で重要だと思います。その点が私にはまだはっきりつかみきれていない点でもあります。

もちろん、ひとつの領域にrelative expected value for choiceと、local fractional income をコードするニューロンが混在している可能性も考えられ、ふたつの論文は、その中の両極端のものを見ている可能性も考えられます。お互いの解析を両方のデータを使ってやって比べてみるということが必要ではないかと思います。あるいは、Sugrue et al (2004) のmatching task 中に報酬量を変化させて、local fractional income と相関した変化と、報酬量の変化に伴う相関との度合いを比べてみると、全体像がもう少し分かるのではないかと思います。例えば、Sugrue et al (2004) Fig.4でみられた相関は、Dorris and Glimcher (2004) で見ていた local なfluctuation に対応し、報酬量の変化はもっと大きなLIP neuron の活動変動を引き起こす可能性も考えられます。また、どちらの論文も population data の示し方が不十分なので、そのあたりをきっちりやればもっと何が起こっているかが良く分かったのではないかと少し残念に思います。

uchida

---

以上です。どうもありがとうございます。編集過程で間違いが混入していたらお知らせください。ひきつづき私もコメントを書く予定です。

■ Neuron 10/14 Glimcher論文追記

11/23 での議論に関する追記。
今回の論文とコメントはゲーム理論に詳しい方が読んでいただくにしてはあまりに細かいところに入り込みすぎたし、元の論文へのアクセスも制限されていて（総合大学のようなところでないかぎり）話の筋を追ってもらうのは難しいと思うので、もうすこし論点のエッセンスを抽出してみるとこうなります：
Payoff matrixが一定な状態で混合戦略でナッシュ均衡にするために非協力ゲームをしている者が変えられるのは自分の行動選択率だけのはずで、自分の効用関数を変えるなんてことはありえないでしょう。しかし今回のinspection gameのようにゲームの途中でinspection costが変化する場合、つまりこれはpayoff matrixが変わるということなので、それを調整してあらたなナッシュ均衡になるときに、自分の行動選択率ではなくて自分の効用を変えて対応するということがありうるかどうか。
これをもしご存知のかたがいらっしゃったらぜひ書き込んでいただけたら幸いです。
このような状況というのはリアルでの経済活動でもあることのはずです。たとえば、二つ競合している販売店があって、ビールと発泡酒のどちらにより売り場を割くかどうかをそれぞれ考えてナッシュ均衡にあります。ビールにかかる税金が法改正で変わってpayoff matrixが変化しました。このときこの競合する販売店が新たなナッシュ均衡になるときに変化するのは売り場面積の比率（行動選択率）だけなのか、それとも売上げにたいする効用関数まで変わるという可能性も考慮しないといけないのでしょうか。と言い換えることもできるでしょう。

■ 以上

でGlimcher論文へのコメントおしまいです。あれこれあって、なんだかんだとこれだけかかってしまいました。mmrlさんには力になっていただきましてどうもありがとうございました。はじめの頃のかなり雑な読みをしていたところよりは核心に近いところまでは行けたのではないでしょうか。
かつてはジャーナルクラブ直前に根を詰める過程で前には読み込めなかったものがやっと浮上してくる、という経験をよくしたものです。これはもちろん研究のための練習なのです。どのくらい考え抜いて、どのくらい本質に近づいたか、そのためにこうやって手を動かして具体的に計算してみたりして、それでやっとイメージが湧いてきて、なにが行われているのかがやっとわかってくるわけです。今回はすこしはそんな感じが出せたのではないかと、なんというか論文を読んでて発見があったと、そんな感じを持ってます。
そうこうしているまに大学院講義まであと一週間を切ってしまいました。来週までそちらについての下調べ関連でこのページが埋まると思います。
追記：たたみにかかってますが、べつにこれで終わりにしたいわけではないので、この論文とコメントへの書き込みを歓迎しております。とくに、いろいろ数式こねくり回しましたが、まだ誤解もいろいろあるはずです。

■ Neuron 10/14 Glimcher論文つづき

"Activity in Posterior Parietal Cortex Is Correlated with the Relative Subjective Desirability of Action." Michael C. Dorris and Paul W. Glimcher

最終回です。電気生理データに関してまとめます。落穂拾いというか、すでに先取りして議論してしまったわけですが。

この論文は基本的にはred(=risky)のchoiceがreceptive fieldに入っていて、そこへsaccadeしたときのデータだけを解析しています(Figure.5とFigure.8を除く)。そうすることによって、現れる視覚刺激と行っている運動とがまったく同じ条件のあいだでinspectionのcost=Iを変えたブロック間でのニューロンの発火パターンの違いを見ようとしているわけです。

この論文のメインのデータはFigure.6です。いま書いたように、視覚刺激も運動もまったく変わらない条件でIをブロックごとに変えると、ナッシュ均衡にあるのでブロック間でのexpected utilityは変わらないけれど、expected value(=reward probability * reward magnitude)やchoice probability(=p(risky))はブロック間で変化している（Figure.3Bのプロットを見ていただければわかる通り）、これが彼らの主張です。それで、LIPニューロンの活動はどうだったか：ブロック間で変化しなかった(Figure.6A,D,E)、だからexpected valueやchoice probabilityをコードしているのではなくてかexpected utilityをコードしているのだ、これがこの論文の最大の知見です。

さて、この論理は正しいかどうか。まず、前回あたりで書いたようにややこしい話なわけです。certainとrislyを比べるのではなくて別々のIでriskyを比べるのは妥当かどうかについてもすでに書きました。そして、expected utilityはブロック間で一定だというけれど、expected valueに関してもブロック間でそんなに違っているわけではないことについても前回示唆しました（だいたい、それならFig.6Aとかにはp(risky)をスーパーインポーズするのではなくて、relative expected value=（1-p(inspect)）/（1.5-p(inspect)）をスーパーインポーズすべきなのですし、それはFig.3Bにもあるように全データを足し合わせると0.35-0.60あたりの比較的小さいレンジに散らばるけど、個々のニューロンでのtrial中のinstantaneousなものとしてはそんなにきれいなものではないでしょう）。

また、この時点ではまだもしかしたらこのニューロンはじつは単なるサッケードニューロンで、運動以外の情報はまったく持っていない可能性もあります。この可能性を排除するために彼らはコントロールの課題としてinstructed trialというのをやっていて、Platt and Glimcher論文のデータの再現をしていて、red targetがgreen targetよりもジュースが多いと固定されているときにはジュースが多い方のtargetで発火頻度が高いことをpopulationデータで示していますが、figure.6Eの全てのニューロンがそういうものなわけではありません（figure.7Bのinstructed trialのデータにあるように、有意な細胞はせいぜい半分くらい。そういうニューロンだけ集めてきて解析する、というのが本当はもっとフェアでしょう）。

彼らが自分の主張を通すためには、expected utilityを変えて、expected valueが一定な条件を設定してやって、そのときはLIPニューロンがexpected utilityに相関していることを示さなければならないのです。なんといっても、タイトルは「PPCはsubjective desirabilityと相関している」なのですから。

それをしようとしたのがFigure.9です。しかしこの論文が明確に避けていることの一つとして、著者はrelative expected valueとニューロンの発火とを関連付けていないのです。彼らがするべきは、ここで算出したようなtrial-baseでのestimate of subjetive desirabilityとLIPニューロンとの相関がtrial-baseでのestimate of expected valueとLIPニューロンとの相関を差っ引いてもあるかどうかなのです。それをしないかぎりFig.9にはなんの意味もありません。

なんにしろ、彼らがここでなにをやっているか：かれらは"subjective desirability"のtrial-by-trialでのばらつきの指標として対戦相手がそのつど強化学習アルゴリズムを使って計算しているものを利用します。

対戦相手（コンピュータ）が次inspectするかnot inspectかのdecisionルールは

対戦相手はtrialごとにp(risky)を強化学習で推定して、これを使って
EU(inspect)=EV(inspect)=p(risky)*(1-I)+（1-p(inspect)）*(2-I)
EU(not inspect)=EV(not inspect)=p(risky)*0+（1-p(inspect)）*2
を計算して
EU(inspect)とEU(not inspect)のどっちが大きいか計算することで
p(inspect)を変化させています。

こんなものでした。mmrlさんご指摘の通り、対戦相手はコンピュータなのでEU=EVです。 そこでFig,9では、この計算で出てきたtrial-baseでのp(inspect)を使って、

EV(risky) = 1-p(inspect)
EV(certain) = 0.5
を計算してrelative subjective desirability
= EV(risky)/（EV(risky)+EV(certain)）
= （1-p(inspect)）/（1.5-p(inspect)）

をtrial-baseで計算させたのです。（ここのアルゴリズムに関する私の理解が間違っていないかぎり。上記のステップの次に強化学習ルールでαを再最適化したというステップがあるのがナゾなのではあるけれど、この過程でpayoffとしてutility functionを推定している、とは考えにくいし）。この時点でsubjective desirabilityと彼らが書いているものはじつはobjective desirabilityになってしまっています。というのもmethodの式(1)-(3)はutility functionが入ってないかぎりexpected valueの式であって、expected utilityの式ではないのですから（いままで書いてきたように、0.5や1ではなくてu(0.5)やu(1)を使う必要がある）。よって、いま私が言った文句は違ったふうに書けます。ここで算出したsubjective desirabilityとは独立なexpected value=objective desirabilityも同様にtrial-baseで計算できますか、と。できっこないわけです。ここで彼らが計算しているのはobjective desirabilityなのですから。

この論文"Activity in Posterior Parietal Cortex Is Correlated with the Relative Subjective Desirability of Action"はどこにもsubjective desirabilityとLIPニューロンの活動の相関(correlation)を見ているところはないので題名は間違っていると私は考えます。最小限の修正でタイトルを直しましょう：タイトルはこうすべきです："Activity in Posterior Parietal Cortex Is Correlated with the Relative Objective Desirability of Action"。なあんだ、Sugrue and Newsome論文と結論は同じではないですか。

まとめましょう。この論文はゲーム理論でのナッシュ均衡になるような興味深い状況においてその行動がゲーム理論から予想されるものであることを示し（しかしより静的な選択理論でも充分説明できる）、LIPニューロンが選択する行動の価値をコードしていることを確認したという点でほぼSugrue and Newsome論文の後追い論文であり、ゲーム理論を応用した本当におもしろい部分の探求には成功しなかった、そういう論文であると考えます。本当におもしろい部分に向かう価値はあると思いますが、おそらくGlimcherはもう懲りたことでしょう。Human fMRIでのデータを蓄積して再びチャレンジする日が来たらすばらしいと思いますが、おそらくそれはLIPの機能を明らかにする、という文脈には置かれないことでしょう。

■ Neuron 10/14 Glimcher論文つづき

"Activity in Posterior Parietal Cortex Is Correlated with the Relative Subjective Desirability of Action." Michael C. Dorris and Paul W. Glimcher

いろいろ復旧してませんが休み終了です。再開します。

今回はいちおうオチ、というか話に収拾がつけてあると思いますが、そこまでの道はかなりぐちゃぐちゃです。

前回の行動データについてさらに続けます。この論文で問題なのは、mmrlさんもコメントでご指摘の通り(11/15および以前の8/31)、expected utility=subjective desirabilityの定量化が明示的には（ぼやかした形でFig.9で扱われているが）まったくなされていないことです。Figure.3を見ながらもう一度考えてみましょう。 Expected valueの比(riskyとcertain間の比）はFigure 3bで明示的に現れています。Expected valueの比を明示的に計算してみましょう。ここではブロック内での平均値に関して。

10/1に書いたように、expected valueを計算するためには別々のoutcome(今回の場合だったらinspectされたときとされないとき)での割合で重み付けをしてvalue(今回の場合だったらジュースの量)を足し合わせます。これをrisky, certainそれぞれでやってみましょう。なお、ここではまだナッシュ均衡のことは考えてません。

riskyのexpected value
 = sum（reward probability(risky) * reward magnitude(risky)）
 = reward probability(risky,inspect) * reward magnitude(risky,inspect)
 + reward probability(risky,not inspect) * reward magnitude(risky,not inspect)
 = p(inspect)*0 + （1-p(inspect)）*1
 = 1-p(inspect)
certainのexpected value
 = sum（reward probability(certain) * reward magnitude(certain)）
 = reward probability(certain,inspect) * reward magnitude(certain,inspect)
 + reward probability(certain,not inspect) * reward magnitude(certain,not inspect)
 = p(inspect)*0.5 + （1-p(inspect)）*0.5
 = 0.5
よってExpected valueの比(riskyとcertain間の比）
 = expected value(risky) / （expected value(risky)+expected value(certain)）
 = （1-p(inspect)）/（1.5-p(inspect)）
なお、Table 1についてさらっと書かれているけれども、
被験者のreward probability for risky choiceというのは
対戦相手がinspectするか否か、p(inspect)で決まっているわけです。
p(inspect)はIのブロック内では被験者がriskyとcertainと選ぶときとで共通です。
よって以下のように書けます。
reward probability(risky,inspect) = p(inspect)
reward magnitude(risky,inspect) = 0
reward probability(risky,not inspect) = 1-p(inspect)
reward magnitude(risky,not inspect) = 1
reward probability(certain,inspect) = p(inspect)
reward magnitude(certain,inspect) = 0.5
reward probability(certain,not inspect) = 1-p(inspect)
reward magnitude(certain,not inspect) = 0.5

この（1-p(inspect)）/（1.5-p(inspect)）がFigure.3Bの横軸で表されているものです。一方で同様な比をexpected utilityでも計算してやることができます。ただし、被験者のジュース量に対するutility functionはここでは未知ですからu()と表記します。フォンノイマン-モルゲンシュテルンのutility functionであるとするならば式変換も多少できます。あと、u(0)=0と見なしておいてよいでしょう。そうすると、

riskyのexpected utility
 = sum（reward probability(risky) * reward utility(risky)）
 = reward probability(risky,inspect) * reward utility(risky,inspect)
 + reward probability(risky,not inspect) * reward utility(risky,not inspect)
 = p(inspect)*u(0) + （1-p(inspect)）*u(1)
 = （1-p(inspect)）*u(1)
certainのexpected utility
 = sum（reward probability(certain) * reward utility(certain)）
 = reward probability(certain,inspect) * reward utility(certain,inspect)
 + reward probability(certain,not inspect) * reward utility(certain,not inspect)
 = p(inspect)*u(0.5) + （1-p(inspect)）*u(0.5)
 = u(0.5)
よってExpected utilityの比(riskyとcertain間の比）
 = expected value(risky) / （expected value(risky)+expected value(certain)）
 = （1-p(inspect)）*u(1) /（（1-p(inspect)）*u(1) + u(0.5)）
 = （1-p(inspect)）/ （（1-p(inspect)）+ u(0.5)/*u(1)）
最後は分子と分母をu(1)で割ってます。

つまり、Expected valueの比とExpected utilityの比とはu(0.5)/*u(1)=0.5のときは等価で、それ以外のときにずれてくるという微妙な差でしかありません。Glimcherが差を出そうとしていたことはこんなにも微妙な差なのです。

とりあえずp(inspect)=0.5のときにu(0.5)/*u(1)を振ってシミュレーションしてみましょう。Expected valueの比は1/2で固定です。Glimcherは今回のSFNでhaman fMRIでutility functionとしてutility = (value^(1-r))/(1-r)を使ってました。r>0でrisk aversive、r<0でrisk seekingです。Indifference curveを作ってrを計算するとrは-0.2-0.4あたりのレンジです。このレンジでu(x)/u(2*x)をだいたいで計算すると、0.40-0.65のレンジ、これを今回の論文のu(0.5)/u(1)に入れてやるとexpected utilityの比は0.43-0.55のレンジに散る、かなり適当な計算ですが、レンジはだいたいあってるでしょう。

さて、いままでの話はp(inspect)が固定している場合で、まだナッシュ均衡は出てきてませんでした。この状況ではexpected valueの方が一定になってしまうわけです、この意味で8/31にmmrlさんが書いてた、expected valueのほうが一定になるのでは？という疑問は正しいわけです。

しかし実際にナッシュ均衡が起こってもp(inspect)=0.5にはならなくてよいし（個体ごとのrisk averseの程度によってずれててよい）、もしtable 1のようにp(inspect)がブロック間で違っているときには（これがナッシュ均衡で起こりうるかどうかは疑問だけど）、expected valueとexpected utilityは今回の実験パラダイムで乖離しうる、しかしブロック間でp(inspect)が共通の時にはexpected valueとexpected utilityは今回の実験パラダイムでは乖離しえない、これがいまから私が書くことのまとめです。

Methodの式(4)-(6)に関しては、対戦相手がコンピュータであり、expected utility=expected valueであるため、ナッシュ均衡にあるときに対戦相手がinspectするときとnot inspectするときとでexpected utilityが等しいことから、p(risky)=Iとなる、これは正しいわけです。しかしいっぽうで、(1)-(3)の方は間違っているのではないでしょうか。もう一回上で使った式を使います。

ナッシュ均衡において、被験者がriskyを選ぶときとcertainを選ぶときとで
被験者のexpected utilityは等しい。よって、
riskyのexpected utility
 = sum（reward probability(risky) * reward utility(risky)）
 = reward probability(risky,inspect) * reward utility(risky,inspect)
 + reward probability(risky,not inspect) * reward utility(risky,not inspect)
 = p(inspect)*u(0) + （1-p(inspect)）*u(1)
 = （1-p(inspect)）*u(1)
certainのexpected utility
 = sum（reward probability(certain) * reward utility(certain)）
 = reward probability(certain,inspect) * reward utility(certain,inspect)
 + reward probability(certain,not inspect) * reward utility(certain,not inspect)
 = p(inspect)*u(0.5) + （1-p(inspect)）*u(0.5)
 = u(0.5)
両者が等しいとき、
（1-p(inspect)）*u(1) = u(0.5)
 p(inspect) = 1- u(0.5)/u(1)

こうなるわけで、p(inspect)は0.5で一定になるというよりは、被験者のutility functionによって0.35-0.60あたりのレンジにあるのではないかと。問題はutility functionがI:inspection costのブロック間で変化しないかどうかです。もし変わってしまえはtable1にあるようにp(inspect)がinspection costによって変化してもおかしくはありません。

だんだんこんがらがってきました。もう少しこのへんの話に材料を与えるために、いままで言ってこなかった話を出しましょう。

この論文のメインの結果はGlimcherの近著のFigure 12.5にもあるように、ナッシュ均衡では別々のinspection costのときのrisky choiceのexpected utilityは等しい、LIPニューロンの活動も一定だった、というものです。しかしこれはそんなにまっすぐな論理ではありません。だって、これまでも書いてきたように、あくまでナッシュ均衡にあるときはそのブロックでのriskyとcertainの選択のexpected utilityが等しいということだけなのですから。もう一つ以上のロジックのステップが必要です。

たとえばI=0.2のときのrisky, certainそれぞれのexpected utilityを
EU(risky,0.2)、EU(certain,0.2)などと書くとしますと、
ナッシュ均衡において、
EU(risky,0.2)=EU(certain,0.2)
EU(risky,0.5)=EU(certain,0.5)
EU(risky,0.8)=EU(certain,0.8)
などが成り立ちます。ここで
EU(certain,0.2)=u(0.5,0.2)
EU(certain,0.5)=u(0.5,0.5)
EU(certain,0.8)=u(0.5,0.8)
でこれはp(inspect)に依存しません。
あとはutility function uがI:inspection costに依存しないこと
が保証されていれば(***)、
EU(certain,0.2)=EU(certain,0.5)=EU(certain,0.8)
が成り立ち、
EU(risky,0.2)=EU(risky,0.5)=EU(risky,0.8)
が成り立つ。

こういうことのはずです。

いっぽうでexpected valueに関してはFig.3BにあるようにI=inspection costに依存します。

たとえばI=0.2のときのrisky, certainそれぞれのexpected valueを
EV(risky,0.2)、EV(certain,0.2)などと書くとしますと、
ナッシュ均衡において、
EV(certain,0.2)=EV(risky,0.2)
となるのはutility function u(x)=xのときだけで、
それ以外では必ずしも成り立っていません。
しかし、
EV(risky,0.2)=1-p(inspect,0.2)
EV(risky,0.5)=1-p(inspect,0.5)
EV(risky,0.8)=1-p(inspect,0.8)
です。もしナッシュ均衡において
p(inspect,0.2) = 1- u(0.5,0.2)/u(1,0.2)
p(inspect,0.5) = 1- u(0.5,0.5)/u(1,0.5)
p(inspect,0.8) = 1- u(0.5,0.8)/u(1,0.8)
が一定ならば(****)、expected valueにおいても
EV(risky,0.2)=EV(risky,0.5)=EV(risky,0.8)
が成り立ってしまいます。実際には
Table 1にあるように、p(inspect)がinspection costに依存するため、
EV(risky,0.2)=EV(risky,0.5)=EV(risky,0.8)
は成り立ちません。

しかし、(***)と(****)とはほとんど等価ではないでしょうか。余計にこんがらがってきた。収拾不可能です。

しかしこれだけは言えます、Glimcherが差を出そうとしていたことはこんなにも微妙な差なのです、ともういちど。

ちょっと絡みすぎました。仮定に仮定を重ねているし（フォンノイマン-モルゲンシュテルンのutility functionが実際の行動から乖離していることについては10/2にやりましたし）。こんなふうに書かなくても、mmrlさんが11/15に書くように、ナッシュ均衡に充分達していない状態で実験しているからtable 1のようにp(inspect)がinspection costに依存してしまっている、これで充分なのでしょう。

ただ、このぐらい書いてみてだんだんわかってきたのは、ナッシュ均衡に充分近づいたとしても、 p(inspect)=0.5にはならずに p(inspect)=u(0.5)/u(1)であると考えた方がよさそうだし、もしp(inspect)がinspection costに依存しないのであったら、riskyのexpected utilityだけではなくて、riskyのexpected valueもブロック間で一定になってしまうのではないか、ということです。つまりこうなると、現在扱ったようなかなり細かいところ（ナッシュ均衡における理論と実際のデータの乖離の理由）まで詰めたうえで考えないとGlimcherのやっていることはexpected utilityとexpected valueとを分けるにあたってまったく検証能力のないテストをやっているのではないか、という疑いがあります。（じつはセミナーでプレゼンしたときにも同様な質問があって、それへの答えをずっと考えていたのです。たぶんこれが答えです。）

もしかしたらGlimcherもすでに論文を作ってゆく過程でこのへんに気付いてしまったのかもしれません。そして、expected valueとexpected utilityを直接比較検証する形を力ずくで避け、expected valueとexpected utilityとが充分分けられていない状況でLIPニューロンがただのchoice probabilityやreward probabilityやreward magnitudeではなくて、expected valueとexpected utilityとが共有しているものをコードしている、という形に落とした、そんなところなのかもしれません。そうなればexpected utilityでなくてsubjective desirabilityにしたところで間違った結論を主張していることになると思いますが。

次回こそ電気生理データを片付けて終わりにします。もうほとんど決着はついた気もするのですが。

■ Neuron 10/14 Glimcher論文つづき

"Activity in Posterior Parietal Cortex Is Correlated with the Relative Subjective Desirability of Action." Michael C. Dorris and Paul W. Glimcher
は今日はお休みということで。mmrlさんの11/15のコメントがとてもヒントになったのでもう少し構成を見直してみるつもりです。

■ Neuron 10/14 Glimcher論文つづき

"Activity in Posterior Parietal Cortex Is Correlated with the Relative Subjective Desirability of Action." Michael C. Dorris and Paul W. Glimcher
実験データに戻ります。今日は行動データに関してまとめます。
前回書いたようにナッシュ均衡にあるときに被験者がriskyの選択をする比率はIによってほぼ決まり、対戦相手の行動自体では決まりません（均衡状態なので対戦相手の行動選択率も均衡にあって、inspectを選ぶ率が計算上p(inspect)=0.5になることがわかっているのですが、実際にはなってません：Figure.2のthin line参照）。これは被験者も対戦相手もヒトであるときですが、被験者がヒト、対戦相手がコンピューターのときおよび被験者がnonhuman primate、対戦相手がコンピューターのときも成り立ちます(figure.3A)。なお、コンピュータが対戦相手のときの行動選択のアルゴリズムにはシンプルな強化学習のルールを使ってます。つまり、被験者がriskyを選択する率p(risky)を推測するのにこれまでのp(risky)から現在の試行の結果がずれた分をp(risky)を変化させてやるわけです。
Expected utilityとexpected valueとの比較、もしくはナッシュ均衡とmatching lawとの比較、といった明示的な形での議論はじつは行動データにしかありません。Figure.3Bでp(risky)がたんにexpected value（reward probability*reward magnitude）による線形的な関数ではないことを示しています。それから、Figure.4Aで[choice probabilityのriskyとcertainとでの比]と[expected value（reward probability*reward magnitude）のriskyとcertainとでの比]をプロットするとslopeが1.32で1より大きい、ということを示しています（統計なし）。Figure.3BとFigure.4Aとは本質的に同じものを違ったやり方でプロットしているだけですので*1Figure.4Aだけを見てもらえば、これは両軸ともlogでプロットしていますので、このslopeが1より大きいということは単にreward valueに対して過剰に適応をしていることを示しており、6/29のコメント欄で私が書いたgeneralized matching lawでのovermatchingをしていることになることを示しているだけです。じっさいここでGlimcherはこの結果がmatching lawでも説明できてしまうことをほとんど認めつつも("It can be true that, in aggregate, behavior during these games appears similar to behavior in nonstrategic envoronments, but ...")、Figure.4Bの結果から被験者のtrial-by-trialのばらつきが対戦相手のローカルなばらつきによって影響を受けることを示して、matching lawで説明されるような静的な過程ではないと言い張ります（"The observation that there was overmatching in the aggregate behavioral strategy, however, should not be read to suggest that the subjects necessarily used a stationary matching-type strategy during this dynamic conflict."）。しかしSugrue and Newsomeの論文はまさにそういったローカルなtrial-by-trialのばらつきもmatching lawで説明できるとしたものでした。このへんは読者が判断することですが、この勝負、Glimcherはまったく歯が立たなかったと思います。Glimcher論文はSugrue and Newsimeが出てなければどれもこれも新しかったけど、スピード競争に負けたがゆえにどんどんneuesがなくなって敗北した、と私は読みます（逆にもしGlimcher論文の方が早ければ、Sugrue and Newsome論文はかなり苦戦したことでしょう。この勝負はそういった命の取り合いであり、私はシュートであると見ています。ちなみにSugrue and Newsome論文はReceived 16 December 2003; accepted 22 April 2004でGlimcher論文はReceived 2 February 2004; accepted 2 September 2004。もちろんGlimcher論文はおそらくその前にNatureかScienceで一、二戦しているわけです）。
では電気生理データはどうか、それは明日つづきます。あと二回くらいで終了する予定。
*1：追記：Figure.3Bの方が真のexpected valueで、Figure.4Aのほうはさらにexpected valueにchoice probabilityを掛け算しているので、等価ではありませんでした。

■ Neuron 10/14 Glimcher論文つづき

"Activity in Posterior Parietal Cortex Is Correlated with the Relative Subjective Desirability of Action." Michael C. Dorris and Paul W. Glimcher
Expected utilityとexpected valueの関係、およびなんでナッシュ均衡がそこに出てくるか、というあたりを説明しましょう。Glimcher"Decisions, Uncertainty, and the Brain: The Science of Neuroeconomics."のp.282-288あたりにちょうどいい説明があるからこれを元にしましょう。（Glimcher本ではチキンランの例を使ってますが、それを今回のinspection gameに読み替えて以下の説明をしています。）
もういちど、どうやってexpected utility(=subjective desirability)の均衡状態を計算しているか繰り返しましょう。

• もし被験者がriskyを選ぶとき、対戦相手がinspectする利得=P(risky)*(1-I)
• もし被験者がcertainを選ぶとき、対戦相手がinspectする利得=（1-P(risky)）*(2-I)
• よって対戦相手がinspectするときの全体としての利得=P(risky)*(1-I)+（1-P(risky)）*(2-I)
• 同様にして、対戦相手がnot inspectするときの全体としての利得=P(risky)*0+（1-P(risky)）*2

対戦相手にとって、inspectするのもnot inspectするのも同じutilityを持っているとき、つまりindifferentであるとき（10/1あたり参照）、対戦相手は均衡点(equilibrium point)にある、と言えます。前回の通り、inspectのときの利得とnot sinspectのときの利得とを等式で結んで、

• p(risly)*(1-I)+（1-p(risky)）*(2-I)=p(risly)*0+（1-p(risky)）*2

これを解くと

• p(risky)=I

となります（追記：mmrlさんの指摘に基づいて式の誤りを直しました。 mmrlさんありがとうございます）。このことは、被験者のp(risky)がIに等しいとき、対戦相手にとってinspectするのもnot inspectするのも等しいexpected utilityを持っている（indifferentである）ということです。言い換えれば、被験者のp(risk)がIに等しいかぎり、対戦相手はinspectするかnot inspectするか気にする動機がないし、inspectするかnot inspectするかは同じくらいよい（もしくは悪い）といえます。逆に言えば、仮にもし被験者があらかじめp(risky)>Iで行動する、と宣言したなら対戦相手はinspectするかnot inspectするかにはindifferentではいられなくて、積極的にinspectするように行動を変化させるべきなわけです。
ここで重要なのは被験者も同様なやり方で均衡点を持つということです*1。被験者と対戦相手のどちらかが最適でないような行動を取ったときには相方は標準的な経済学的最適化問題を解くことになるわけですが、両者が最適解を得ようとするかぎり、両者それぞれは均衡点にたどり着きます。このようにして計算された均衡点は（被験者にとって）riskyかcertainか、（対戦相手にとって）inspectかnot inspectか、がそれぞれにとってindifferentである（等しいexpected utilityを持つ）行動選択パターンを決定します。このようなindifferent pointこそが被験者と対戦相手とがたどり着く均衡状態（ナッシュ均衡）のことなわけです。("Decisions, Uncertainty, and the Brain: The Science of Neuroeconomics." p.285-286をinspection game用に置き換えて超訳、ですのでこれは引用ではなくて改変しているので＜blockquote＞に入れてません。)
んで、とくに明示されていないので注意すべきだと思うのですが、問題なのはここでの利得と言っているやつはただのジュースの量なので、utilityそのものではないのです(たんなるexpected valueですよね)。じっさい、0.30mlのジュースをもらうのが0.15mlのジュースをもらうのの2倍うれしいのかどうかはそういうutility functionを作って検証しなければならないわけです*2。だから、ここでの話をきっちりutilityに変換するためにはinspection gameでのpayoffマトリックスの被験者の利得の0、0.5、1というやつをu(0)、u(0.5)、u(1)というutility function uを通したものに変換してやらないといけないわけです。また、そういうわけですから、じっさいのデータでもp(riskt)=Iにまったく等しくならなくてもよいわけです。ただし、それでもこのinspection gameで均衡状態にあるときにriskyを選ぶexpected utilityとcertainを選ぶexpected utilityが等しい、というのは妥当です(どこまでいったら均衡状態なのかの基準はさておき)。もっとも、そのときのexpected utilityを上記の利得（たとえばP(risky)*(2-I)とか）そのものとして計算するのはやはり間違っているといえます。このように、実際のutility functionを計算していない今回の実験では、expected utilityそのものを計算することはできません。ナッシュ均衡では等しい、ということしか言えません。これがたぶん11/12のコメント欄でmmmmさんがお書きになったことでないでしょうか（「utility functionが既知であると言えない場合、economistsは"expected utility"という用語を使うことを認めない」、これなら意味は通る気がします）。
よって、expected valueとexpected utilityとの差はじつはかなり微妙なものであるはずだし、明示的にこの問題を解こうとしたら被験者ごとのutility functionを作成する方向へ行くのが筋だと思うのです（今年のSFNではhuman fMRIでそういう結果を出していましたが、もちろんこれはヒトでのstudyだからできることであるわけです）。また、Glimcher本では数学的に言うときにはexpected utilityという言葉を使っているけれども、場所によっては"value"という言葉を安易に使っているところもあり、おそらくexpected valueとexpected utilityとの違いにそんなに敏感ではなかった節がありますし、もともとPlatt and Glimcherで扱ったようなdecision variable(reward magnitude, reward probability, choice probability)を包括して説明できるものを探してナッシュ均衡に行ったはずです。Sugrue and Newsome論文が通っていなければそれでも話は通っていたのかもしれませんが。
ああ終わらない。

*1：もし対戦相手がinspectするとき、被験者がriskyを選ぶ利得=P(inspect)*0
もし対戦相手がnot inspectするとき、被験者がriskyを選ぶ利得=（1-P(inspect)）*1
よって被験者がriskyを選ぶときの全体としての利得=P(inspect)*0+（1-P(inspect)）*1
同様にして、被験者がcertainを選ぶときの全体としての利得=P(inspect)*0.5+（1-P(inspect)）*0.5
んで、被験者がriskyを選ぶのもcertainを選ぶのもindifferentなときは
P(inspect)*0+（1-P(inspect)）*1=P(inspect)*0.5+（1-P(inspect)）*0.5
これを解くとP(inspect)=0.5となり、じつは定数になります。じっさいのデータはそうなっていないので、被験者の選択はナッシュ均衡の周りでふらふらと揺れていると考えた方がたぶんよいのでしょう。これは私の意見。
*2：確認のため、risk averseな例について書いておきましょう。(A)ジュース量0.5で100%出るときと、(B)ジュース量1で50%、ジュース量0で50%のときとどっちがいいですか？ (A)のexpected utilityはu(0.5)で、(B)のexpected utilityはu(0)*0.5+u(1)*0.5です。Utility function uがu(x)=log(x+1)で定義されるとします（この関数は上に凸だからrisk averseな例のモデルによく使われます）。すると両者のexpected utilityは(A)>(B)となります（log(3/2)>log(2)*0.5）。もし、(B)でジュース量1の比率がlog(3/2)/log(2)だと(A)と(B)とはindifferentなわけです。

■ Neuron 10/14 Glimcher論文つづき

"Activity in Posterior Parietal Cortex Is Correlated with the Relative Subjective Desirability of Action." Michael C. Dorris and Paul W. Glimcher
今回の論文紹介は長いですが、それはこのあいだ私が行ったジャーナルクラブでの説明をほとんどそのまま転載しているからです。論文読んだほうが早いかもしれません。
まず、最小限必要なゲーム理論の初歩について書きましょう。ナッシュ均衡、純粋戦略、混合戦略、のキーワードの内容を知っていれば読む必要はありません。
「囚人のジレンマ」という言葉を聞いたことがあるでしょうか。泥棒の共犯AとBが捕まって別々の部屋で尋問を受けてます。AとBとは通信の手段がありません。AとBとはそれぞれ黙秘するか自白するかの選択を迫られています。もしAが黙秘してBも黙秘したら二人とも懲役2年、もしAが自白してBも自白したら二人とも懲役10年、もしAが自白してBが黙秘したらAは釈放、Bは懲役15年、もしAが黙秘してBが自白したらAは懲役15年、Bは釈放です。（追記：説明文がpayoffマトリックスと合致していませんでしたので直しました。Tさんご指摘ありがとうございます。)
以上をpayoffマトリックスにまとめるとこんなテーブルになります。行はAが黙秘するか自白するかの選択、列はBが黙秘するか自白するかの選択で、各マスにはそれぞれの選択での損得勘定（各マス内の左下がAの損得、右上がBの損得）が入ってます。釈放が0で懲役15年は-15、という調子です。

		泥棒B
		黙秘		自白
泥棒A	黙秘	-2 -2		0 -15
	自白	-15 0		-10 -10

では、AとBがお互いに連絡を取れないとして、それぞれが合理的に考えるとしたらどういう選択をするでしょうか。泥棒Bが黙秘したときには、泥棒Aとしては黙秘(-2)よりも自白(0)の方がよい選択ですし、泥棒Bが自白したときには、泥棒Aとしては黙秘(-15)よりも自白(-10)の方がよい選択です（泥棒Aにとってよい選択を赤で表記）。どちらにしろ泥棒Aが合理的に考えると自白する方が得策であるという結論になるでしょう。同様にして、泥棒Bも自白した方が得策という結論になります（泥棒Bにとってよい選択を青で表記）。すると、この赤文字と青文字の重なったマスの部分、つまり互いに自白した場合(-10,-10)が「お互いが合理的な策を取った（ので悔いがないはずの）とする安定状態」で、こういうのをナッシュ均衡の状態にある、といいます。
じゃあなんで囚人の「ジレンマ」と言うかといったら、それはAとBとが通信可能ならお互いに黙秘する（二人とも懲役2年）という戦略がとれたはずだからです（こういうのはパレート平衡という別の概念です）。ま、それはそれとして、お互いに手の内を明かさない対戦型のゲームではお互いが合理的に選択した、と言い得る状態がナッシュ均衡なわけです。
今のたとえ話はたった一回きりの選択（黙秘するか自白するか）なわけですが、普通ゲームだったら繰り返し選択をします。わかりやすいのがジャンケンで、こんどは二人の対戦相手AとBとは三種類の行動の選択肢があります。Payoffマトリックスはこんな感じです。勝ったら+1、引き分けが0、負けたら-1です。

		B
		グー	チョキ	パー
A	グー	0 0	-1         1	1 -1
	チョキ	1 -1	0 0	-1 1
	パー	-1 1	1 -1	0 0

んで、こんどはたった一回の勝負に関してはナッシュ均衡はありません。ジャンケンに必勝の手などありませんから。しかし、何度もこのゲームを繰り返すのであれば、いちばん良い手はグーとチョキとパーそれぞれを確率1/3ずつで出すのが一番よい手であることは予想がつくと思います。これは対戦相手AとBそれぞれで成り立ちます。よってある一回の勝負でその選択が一番良いか（純粋戦略）、ではなくて繰り返しの勝負でどういう比率で選択をするのが一番よいか（混合戦略）という形に拡張したときのナッシュ均衡はジャンケンの場合お互いがグーとチョキとパーそれぞれを確率1/3ずつで出す、というものです。このような混合戦略ではナッシュ均衡となるような解が必ずあることが知られています（これが以前言及した、NashがPNASに書いたたった1ページの論文の内容です）*1。今回の論文で使っているinspection gameもこういう混合戦略でのナッシュ均衡を扱っています。
んでやっと今回使っているinspection gameについての説明ですが、ま、「ダウト」みたいなもんです。被験者はcertainとriskyの二つの選択肢を選ぶことができて、certainは100%確実に0.15mlジュースがもらえるのにたいして、riskyではその二倍(0.30ml)かもしくはまったくなし(0ml)です。riskyの結果は対戦相手の行動が握っていて、対戦相手がinspectしたときに被験者がriskyを選んだときはまったくジュースがもらえなくて、対戦相手がinspectしなかったときに被験者がriskyを選んだときは二倍のジュース(0.30ml)がもらえるわけです。いってみればinspectを選択するのが「ダウト」を発することです。もちろん「ダウト」するにはそれだけのコストがかかります（そうでなければいつでもダウトしてればいいわけだから）。Payoffマトリックスにすると以下の通り。

		対戦相手
		inspect	not inspect
被験者	certain	2-I 0.5	2 0.5
	risky	1-I 0	0 1

Iは150trialくらいのブロックごとに実験者によって0.1-0.9の範囲で変えられます。たとえばI=0.1だと対戦相手はinspectするコストが低いのでどんどんinspectします。すると、riskyの選択をしてもたいがいダウトされてしまって損なので被験者がriskyを選択する確率は減ります。一方でI=0.9だと対戦相手はinspectするコストが高いのでほとんどinspectしません。このときはriskyの選択をしたらもらい放題ですから、被験者がriskyを選択する確率は上がります*2。
ナッシュ均衡では対戦相手がinspectするときとnot inspectするときとでexpected utilityが等しくなります。これは被験者がriskyを選ぶ確率をp(risky)として、p(risly)*(2-I)+（1-p(risky)）*(1-I)=p(risly)*2+（1-p(risky)）*0と書けて、これを整理すると
p(risky)=I
となります。つまり、被験者と対戦相手が非協力的に自分の利益を最大化するように行動するとナッシュ均衡になって、そのとき被験者がriskyを選択する比率はIのみによって決まる（対戦相手の行動によらない）わけです。

それで行動データ(figure 2、3A)を見ると、たしかにだいたいそうなっています。
ここらで続きは次回。
（追記：Nash equilibriumの訳を「ナッシュ平衡」ではなくて「ナッシュ均衡」に直しました。）

*1：なお、このNash論文での角谷の不動点定理を用いた証明に関する詳しい解説がhttp://www16.ocn.ne.jp/~hsasaki/genkou.htmlの「初歩からのゲーム理論」のところにあります。
*2：なお、このpayoffマトリックスのIに0.1から0.9までを代入してみれば、純粋戦略でナッシュ均衡となるような解はないことがわかります。つまり、対戦相手がinspectするときには被験者はcertainのほうがよいし、対戦相手がnot inspectのときには被験者はriskyのほうがよい。一方で、被験者がcentainのときには対戦相手はnot inspectのほうがよいし、被験者がriskyのときには対戦相手はinspectのほうがよい。お互いが得する手はないわけです。

■ Neuron 10/14 Glimcher論文

というわけでやっとこさGlimcher論文にコメントです。
"Activity in Posterior Parietal Cortex Is Correlated with the Relative Subjective Desirability of Action." Michael C. Dorris and Paul W. Glimcher
Glimcherは何度も出てきましたが、Platt and GlimcherでLIPがそれまでattention(ME Goldberg)かintention(Andersen)か、という論争をしていたところにDecisionである、という話をはじめて持ち込んで成功させた人、と言えるでしょう。LIPがdecisionに関わっているか、という話自体は1996 PNASでShadlen and Newsomeが最初に言い出したことではありますが、のちのrandom dotによるperceptual decisionの結果が出てくるまでは大きな進展はなかったはずです。Glimcherはその前はDavid Sparksのところで上丘のニューロンが眼球運動を開始する以前から活動を開始するのを見つけていて(Nature '92; Schallより前にselectionと言った論文)、知覚でも運動でもない、自由意志に近いものを見よう、というポリシーははっきりとしています。
そういえば、Glimcherの近著、"Decisions, Uncertainty, and the Brain: The Science of Neuroeconomics." の前半はまさにシェリントンの反射学説からそのような自由意志を見つけ出そうとする流れについて概説する、という内容です。ちなみにこの本の後半は上述のLIPがattentionなのかintentionなのかという論争をGlimcherがdecisionである、として仲裁、解決したかのような都合のよい史観とゲーム理論の初歩、そして今回の論文のエッセンス（Figure 12.5）までで終わります。題名にneuroeconomics(神経経済学)とありますが、体系的な本ではありませんし、あくまで今回の論文までのpreludeがこの本である、と考えるのがよいのではないかと。（ですので、私は正直言ってこの本の訳書を出版する意義はあまりないように感じます。Human fMRIの結果、とくに以前話題になったペプシチャレンジのようなneuromarketing的なアプローチあたりこそが世で「神経経済学」という言葉に期待するものではないでしょうか。そういうことがまったく書かれていないことを知ったら読者はさぞがっかりするかと。） あ、飛ばし読みで言っているので以上のことは信じないでください（人生は短いのでそんな時間はない）。
1st authorのMike DorrisはカナダのQueen's UniversityのDoug Munozのところで上丘での電気生理でいい論文を出してきました。そのあとにGlimcherのところ(new York University)へ行ってやった仕事がこれです（SFNでの発表自体はすでに2002年に出ています*1）。
んで、この論文のエッセンスは上記のとおり、Glimcherの近著のFigure 12.5です。つまり、被験者とコンピュータがあるゲームを対戦します。このゲームは繰り返すうちに被験者とコンピュータとのあいだでナッシュ均衡になります。実験者が決めた条件によって違った均衡状態になります（ある行動の選択率が変わる）がナッシュ均衡なのでexpected utilityはその条件間で不変です。一方で、その行動の選択率が変わっているので条件間でexpected valueは変わっています。さて、このゲーム中のLIPニューロンの活動はexpected utilityとexpected valueのどちらと相関していたか：expected utilityでした、つまり、違った条件間でもナッシュ均衡にある限りLIPニューロンの発火頻度は不変だったのです。以上。
たぶんそう言いたかったのですが、じつはかなりその辺はあいまいにしてあって、要旨での主張は、LIPの活動はsubjective desirabilityと相関していて、reward magnitideやreward probabilityやresponse probabilityのcombinationにはよらない、というところまでなのです。このへん微妙なラインでして、慎重にものを言う必要がありますが、大胆に行きましょう。
では、順を追ってもう少し説明しつつ（ナッシュ均衡についても説明しつつ）、彼らの主張が本当に正しいかを検討してみましょう。とくにこの論文を読むには、以前採りあげたSugrue and NewsomeによるScienceでの「LIPニューロンがexpected value(!)と相関している」という主張とあわせて批判的に読む必要があります。というかGlimcher論文がNature,Scienceを落ちたのは恐らくはこの批判を充分跳ね返すことができなかったからであり、このため今回のGlimcher論文では"expected utility"という言葉を一回も用いていません（検索して確認しました）。全部"subjective desirability"という言葉に差し替えることで両者の比較をあいまいにしたのです。そしてそれは明らかにレフェリー（Newsome or Shadlenが入っている確率は150%でしょう）による指示 and/or かGlimcherによる妥協案だったはずです。
うーむ、前置きが長い、つづきは次回（エー）。

*1：ところでこれの題名は"expected value"なんです。D. LeeおよびNewsomeそれぞれの論文が'04で出てしまい、それを追っかける形でなんとか'04で出版に漕ぎ付けたDorris and Glimcherの苦労と後悔と怒りが忍ばれます。

■ Neuron 10/14

"Neural Correlates of Behavioral Preference for Culturally Familiar Drinks." 「コカコーラとペプシはほぼ同じ化学組成をしているのに、人々は決まってどちらか片方への強い嗜好を示す。」でもってこの二つを飲み比べているときのヒトの脳の活動をfMRIで調べて、(1)どちらがコーラでどちらがペプシかわからない条件と(2)どちらがコーラでどちらがペプシかわかる条件とで比較しました。すると、コーラの場合はコーラであることを知っているかどうかで活動部位が大きく違っていたのに対して、ペプシでは活動部位に差は見られませんでした、これが結果。つまり、ペプシよりもコーラのほうが広告戦略がうまくて嗜好や脳の活動にブランド力が影響を与えている、ということになります（著者の意図を汲めば）。
うーむ、すごい…天下のNeuron誌にこんなのが出てくるとは…というかコカコーラやペプシの会社はどう反応しているのでしょうか。

• コカコーラのプレスリリースにはなんにもない様子。
• ペプシのプレスリリースにもなんにもない様子。
• Times Online 10/14 "Coke or Pepsi? In fact it's all in the mind."
• WebMD Health "Cola Preference: Branding Sways the Brain."

っつーか、これこそぜったいにイグ・ノーベル賞を意識していると見ましたがね。
追記：ご隠居のところの10/15に関連記事があります。なるほど、たんなるおバカ論文ではないんですな。マーケティングに脳機能イメージングを使うという倫理的問題と（ある人たちにとっては）ビジネスチャンスがあるわけですな。

■ Neuron 10/14

"Activity in Posterior Parietal Cortex Is Correlated with the Relative Subjective Desirability of Action." Michael C. Dorris and Paul W. Glimcher
被験者vs.コンピューターでナッシュ均衡になるようなゲームをさせて、そのときのLIPのニューロン活動を調べたら、それは報酬の確率や大きさ、反応する確率などのパラメーターではなくて、その行動の主観的なdesirability（たぶんこいつが=expected utility）をコードしているのを見つけた、というものです。
例のGlimcherの論文（夏のワークショップ　「意志決定：心の物質基盤」でGlimcher3.pdfとしてin submissionだったやつ）がNeuronになって出てきました。Nature, Scienceは落っこちたようですね。2月にsubmitして、revisionが7月でacceptが9月ですか。かなり難航した様に見受けられます。Neuroeconomicsのコメンテイター（ゴメン、ウソ）としてはこれは採りあげるべきでしょう。なんにしろやってみます。お待ちを…科研費の申請をSFN前に出さなければならないので、たぶん遅れます。

■ Expected valueとexpected utility

つづき。
(3) 200年後の1944年になってフォンノイマンとモルゲンシュテルンがこれを数学的に厳密な形であつかいます。つまり、5つのaxiom(completeness, transitivity, continuity, monotonicity, substitution)が満たされるかぎりにおいて、

expected utility = sum(utility of outcome(i) * probability of outcome(i) )

となるようなexpected utility functionが存在して、これを比較してどちらの選択のほうがpreferredであるかを決めることができる、というものです。逆にいえば、utility functionの計算と比較というのは5つのaxiomがvalidでないときには意味がない（かも知れない）ということです。このような定式化によって、実際の人間行動がこのaxiomを満たしていない例をあげることができるようになったわけです。
(4) この定式化はさらにSavage(1954)による"subjective expected utility"において、さらにaxiomが付け加えられ、式は実際の確率ではなくてsubjectiveな確率によって置き換えられます。

expected utility = sum(utility of outcome(i) * subjective probability of outcome(i) )

(5) フォンノイマン-モルゲンシュテルン-Savegeのaxiomが成立しない例としてAllaisのパラドックス(1953)というのがあります。それはこうです：

[A] 100万円必ずもらえる
[B] 10%の確率で500万円もらえる、89%の確率で100万円もらえる、1%の確率で0円になる
から選択するとしたらどうします？ [B]はほとんどの場合は[A]と同じで、残りのうちの1/11で0円になることがある、と考えるとわざわざ危ない橋を渡るより[A]で確実にいったほうがよさそうではないですか？ 期待値は[A]が100万円、[B]が139万円ですからexpected valueではなくてexpected utilityに基づいて選択しているわけです。これ自体は前述のrisk aversionの現象ですが。一方で、
[C] 11%の確率で100万円もらえる、89%の確率で0円になる
[D] 10%の確率で500万円もらえる、90%の確率で0円になる
だとしたら迷わず[D]を選ぶでしょう。期待値は[C]が11万円、[D]が50万円です
ところで[A]のexpected utilityが[B]のexpected utilityより高いことを[A]>[B]と書くとすると、axiomの五番目(substitution)を使って式変形すると[C]>[D]となって[C]を選ぶほうがexpected utility的には高いことになってしまいます。これはおかしい。

これがパラドックスです。ようするに、五番目のaxiom(substitution)が成立しないことがあることを示しているのです。だから定式化することが重要なのですな。
(6) KahnemanとTverskyのプロスペクト理論はフォンノイマン-モルゲンシュテルンの定式化とは別の方向からのアプローチです。彼らのバックグラウンドは心理学であり、不確実性がある状況で実際に人間がどのような選好を行うかの実験データを蓄積しました。そのような実験結果に基づいた実際の人間の行動のバイアスをとりこんだmodificationを加えて、予測可能性を上げたexpected utilityの定式化をした、というのが彼らのプロスペクト理論の核でして、Kahnemanがノーベル経済学賞を授与された理由でもあります。

expected utility = sum( (utility of outcome(i) - reference point) * decision weight function)

前述のrisk aversionにもあったように損のutilityの大きさ=得のutilityの大きさ*(-1)ではないわけで、valueからutilityへの変換の関数は正（得）と負（損）とでslopeが変えてあります。また、実験結果から、人間はutilityの大きさそのもので判断しているのではなくて、あるreference point（たとえば1万円の持つutility）からどのくらいずれているかで有効なutilityの大きさを評価していることがわかっており、これも取り込まれています。また、主観的確率に関しても実験結果から、われわれは確率の低い事象を過大評価し、確率の大きい事象を過小評価するというバイアスがあり、これによって確率の代わりに"decision weight function"という形で重み付けが行われます。そしてこのような定式化が実際の人間の行動を予言するのに大いに成功したというわけです。
つまり、フォンノイマン-モルゲンシュテルンの定式化はaxiomatic:公理的であるのに対して、KahnemanとTverskyの定式化はdescriptiveなものなわけで、定式化の動機が違うわけです（理想状態の定式化と実際の行動の予測）。じっさい、KahnemanとTverskyも両方のアプローチが必要であるとしています。
参考にしたサイト：

• "HET (THE HISTORY OF ECONOMIC THOUGHT WEBSITE)"
• "2002年ノーベル経済学賞 Advanced information(pdf)"
• "The von Neumann-Morgenstern Theory of Rational Choice under Uncertainty."
• "EconPort - Handbook - Decision-Making Under Uncertainty - Von Neumann-Morganstern Expected Utility."
• "EconPort - Handbook - Decision-Making Under Uncertainty - Allais Paradox Experiments."
• "EconPort - Handbook - Decision-Making Under Uncertainty - Risk Aversion."
• "Utility Theory (Syllabus Topic XII)"
• "PSYC 4135/5135 Judgment, Choice, and Decision Making Spring, 2001."
• "John Quiggin: Expected utility."
• "Cognitive Processes Lecture Notes."
• "Expected value, expected utility and multi-attribute utility theory."
• "PSY 355: Cognition."

■ Expected valueとexpected utility

> なんにしろ、expected valueとexpected utilityの違いについてもうちょっと整理してみる必要があります。パスカルからベルヌイ。[ミクロ経済学での限界効用]と[フォンノイマンとモルゲンシュテルンのutility theory]と[カーネマンのprospect理論]との関係。
んで、調べてみたら余計にこんがらがってきたりして。
そもそも[ミクロ経済学での限界効用]の話のような、あるミカン3個+リンゴ5個の効用はミカン10個+リンゴ1個とindifferentである、というような関係は不確定性のない状況でのdecisionです。なので、今回のWolpertの話にしてもミクロ経済学の教科書的な知識の範疇で済んでしまう話だったようです。
一方で、私の興味を引いていたのは不確定性のある状況でのdecisionの話でした。こちらを順を追って書いていきましょう。
不確定性がある、とはつまり確率の要素が入ってくるということです。以下のことは私なんかがまとめるよりはもっとましなものがあることでしょう。ツッコミ歓迎。
(1) まず、パスカルが最初にexpected valueという概念を使用しました。Valueという言葉が入ると「価値」という重みを持った言葉な感じがしますが、何のことはない、「期待値」ですよね。神様がいるかどうかの賭けに関してはググってもらうとして、つまり、

条件1: 確率1/2で100万円、確率1/2で200万円もらえる、
条件2：確率1/4で100万円、確率3/4で200万円もらえる、

で条件2を選ぶのは条件1の期待値150万円よりも条件2の期待値175万円のほうが大きいからです。でこういう計算

expected value = sum(value of outcome(i) * probability of outcome(i) )

を最初にしたのがパスカルだったと。
(2) しかし、ベルヌイがサンクトペテルブルグのパラドクス、というやつを提出します。これもググってもらうとして、要は、ある有限のお金を賭けると期待値としては無限大のお金が得られるような賭けの例を提出するのです。このような賭けにはたとえ出さなければならないお金が100万円だとしても得られる期待値は無限大のはずだからみんなやるはずなのに誰もやらない、なぜか。それはお金の価値(value!)が二倍になったら二倍得だったかというとそういうわけではなくて金額が大きくなるごとにお得度は目減りしてゆくから、という説明でこのパラドックスを解消します*1。つまり、このような計算をするときには得られるお金の値(value)ではなくて、効用(utility)を考えなければいけない、というわけです。このような効用uと金額xとの関係はu=log(x)のような単調増加でだんだんslopeがぬるくなってくるカーブでモデル化することができて、このことがわれわれが多くの場合にrisk averse（後述）であることの原因でもあります。しかし基本的な式は同じで、valueの代わりにutilityに置き換わっただけです。

expected utility = sum(utility of outcome(i) * probability of outcome(i) )

Risk aversionについて。もし1000円出したら1/2の確率で0円に、1/2の確率で2000円になるとしたら賭けてみます？ このぐらいならやる人はいるかもしれない。でも、もし500万円出したら1/2の確率で0円に、1/2の確率で1000万円になるとしたら賭ける人は減りますよね。これがrisk aversionです。それは500万円損すること=500万円得すること*(-1)ではないからですよね。一方で1000円損すること=1000円得すること*(-1)に近かったりします。これはutility u=log(x)のような形をしていることによって説明できるわけですが、またプロスペクト理論のところで出てきます。
つづきます。
(3) フォンノイマンとモルゲンシュテルン
(4) Savage(1954)による"subjective expected utility"
(5) Allaisのパラドックス(1953)
(6) KahnemanとTverskyのプロスペクト理論

*1：しかしパスカルの神の賭けといい、サンクトペテルブルグのパラドクスといい、無限大の概念が入ってくるのが非常に気持ち悪いんだけれど。

■ PLoS biology 10月号

"A Neuroeconomics Approach to Inferring Utility Functions in Sensorimotor Control." Daniel M. Wolpert。タイトルの"Neuroeconomics"が入ってきたという、いかにも流行に合わせてみました、という感じだけどどうか。
Daniel M. Wolpertはこれまで何度か出てきましたが、内部モデルの人です。運動を最適化させるような課題を人間の被験者に行わせて、それをモデル化するということをやってきたわけです。最近のNatureではベイジアン的な最適化が行われていることを示していました。今回はその課題をforced choiceにして、その選択が運動課題の二つのパラメータ（かかる力の最大値Fとduration T）によってどう変わるかの三次元プロットを作ってやりました。つまり、レバーを動かしてカーソルを移動させるタスクで途中でレバーに力がかかるようにします。二組のFとTの組み合わせでどちらが楽にカーソルを目標値に持っていくことができたか被験者に報告させます。この選択率からutility functionを計算してやります。 このプロットのパターンは被験者がF*Tを最小化している、またはFを最小化しているときに予想されるパターンとは異なっており、もっと非線形であるようだ、というのがこの論文の結論です。
二つのパラメータをふって選択をさせることによってeconomicsの応用と言える要素を導入しているわけです。mmrlさんの8/31のコメントからすると、Dorris and Glimcherの場合、二つのターゲットがあって、reward probabilityとreward量とをふってやって、どっちを選択するかを調べてやることでutility functionを計算してやって、indifference curve上でのutilityが等しい二条件でかつ行動選択率が違うような条件でLIPニューロンの活動を比較する、および行動選択率は同じだけれどuntilityが違うような二条件を比べてやった、ということになるのでしょう。繋げてみるとなんとなくわかってきた。Utilityは選択そのものによってdefineされ、valueはパラメータの掛け算によってdefineされる、と言えばよいか(<-読んでから言え、俺)。
なんにしろ、expected valueとexpected utilityの違いについてもうちょっと整理してみる必要があります。パスカルからベルヌイ。[ミクロ経済学での限界効用]と[フォンノイマンとモルゲンシュテルンのutility theory]と[カーネマンのprospect理論]との関係。調べてみました。これについては明日書きます。
ところでutility function(効用関数)の三次元プロットがあって、それのうちの同じutilityの点をつないだのがindifference curve(無差別曲線)なわけです。例えて言えば、地図は緯度と経度の二つのパラメータによってそこの標高が決まります。同様に二つのパラメータ（消費財）から効用が決まります。その地図で同じ色が塗られているところをつないだのが等高線です。同じ大きさの効用の場所の線をつないだのがindifference curveです。いわば「等効用線」ですよね。気圧の等高線のほうが毎日天気予報で見てるからイメージが湧くかもしんない。
しかし、この「無差別曲線」という広く使われているらしい日本語訳って変ですよねえ。だってindifferenceって「差がない」という意味ではなくて、"lack of interest"（無関心）なわけですから。"Involving no preference"とか"unbiased"とかの語義のほうが近いのだろうけど。中立線、なんてどうだろうか。そういえばindifferent electrodeの訳は不関電極で直訳っぽいけど、これはこれで意味がわかりませんな。難しい。

■ Neuroeconomics(神経経済学)サイトまとめ

mmrlさんの9/4へのコメントを元に。

• 7/4のところでリンクした"Brain Waves"からいくつか辿れます。
• "Neuroeconomics and neuromarketing labs, faculty, researchers, seminars, and consulting." by Richard L. Peterson。スタンフォードを出て、コンサルタント会社をやっているらしい。
• "Center for Neuroeconomics Studies." by Paul J. Zak @ Claremont Graduate University
• "Neuroeconomics" Kevin McCabeによるblog (TypePad使用）だが、ほとんど更新止まってます。
• "Neuroeconomics." From Wikipedia
• "NeuroEconomics 2004." Read Montague @ The Human Neuroimaging Laboratory at The Baylor College of Medicineによるらしい。

■ 越後湯沢のワークショップ

8/31のエントリで質問した「意志決定：心の物質基盤」でのGlimcherの話に関するレポートをmmrlさんが書き込んでくださいました。8/31のコメント欄にあります。どうもありがとうございます。
現在submit中であるDorris and Glimcherのドラフトが脳と心のメカニズム 第5回　夏のワークショップ　「意志決定：心の物質基盤」のサイトから落とせます（気付かなかった……）。03年7月のドラフトがhttp://www2.bpe.es.osaka-u.ac.jp/event/summerws2004/papers/Glimcher1.pdfで、04年5月のドラフトがhttp://www2.bpe.es.osaka-u.ac.jp/event/summerws2004/papers/Glimcher3.pdfの模様。
ノーベル経済学賞を取ったダニエル・カーネマンのプロスペクト理論に関しての言及（日本語）は
http://members.aol.com/mnkctks/dokusho0403.html
http://www.hefx.ne.jp/annai/yougo_h.html
で見つかります。

■ 越後湯沢のワークショップ

「意志決定：心の物質基盤」参加した方、Glimcherの話はどうでしたか？ 前半が新著"Decisions, Uncertainty, and the Brain: The Science of Neuroeconomics." からデカルトとか引っ張り出して語っていることまではキャッチしております。（新著の第一章がhttp://mitpress.mit.edu/books/chapters/0262572273chap1.pdfで読めるようになってます。たぶんこれ。） Newsome論文でもreferしてましたが、Mike Dorrisがfirst authorでゲーム理論的にやってるやつが昨年のSFNに出てましたけど（去年はSFN行ってないんで内容は知らないんですが）、あれの進展はあったんでしょうか？ ご存知の方、レポート期待します。

お勧めエントリ

• 細胞外電極はなにを見ているか(1) 20080727 (2) リニューアル版 20081107
• 総説 長期記憶の脳内メカニズム 20100909
• 駒場講義2013 「意識の科学的研究 - 盲視を起点に」20130626
• 駒場講義2012レジメ 意識と注意の脳内メカニズム(1) 注意 20121010 (2) 意識 20121011
• 視覚、注意、言語で3*2の背側、腹側経路説 20140119
• 脳科学辞典の項目書いた 「盲視」 20130407
• 脳科学辞典の項目書いた 「気づき」 20130228
• 脳科学辞典の項目書いた 「サリエンシー」 20121224
• 脳科学辞典の項目書いた 「マイクロサッケード」 20121227
• 盲視でおこる「なにかあるかんじ」 20110126
• DKL色空間についてまとめ 20090113
• 科学基礎論学会 秋の研究例会 ワークショップ「意識の神経科学と神経現象学」レジメ 20131102
• ギャラガー＆ザハヴィ『現象学的な心』合評会レジメ 20130628
• Marrのrepresentationとprocessをベイトソン流に解釈する (1) 20100317 (2) 20100317
• 半側空間無視と同名半盲とは区別できるか？(1) 20080220 (2) 半側空間無視の原因部位は？ 20080221
• MarrのVisionの最初と最後だけを読む 20071213

月別過去ログ

[2024]

5|

4|

3|

2|

1|

[2023]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2022]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2021]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2020]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2019]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2018]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2017]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2016]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2015]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2014]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2013]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2012]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2011]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2010]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2009]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2008]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2007]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2006]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2005]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2004]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2003]

12|

11|

8|

7|

[2001]

10|

8|

6|

5|

4|

2|

[2000]

12|

9|

8|

7|

6|

3|

2|

1|

[1999]

9|

8|

7|