pooneilの脳科学論文コメント

■ Dorris and Glimcher (2004)とSugrue et al(2004)(mmrlさんより)

mmrlさんが1/4コメント欄で言及していた計算をしてくださったものが届きました。許可をいただいたので以下に掲載します。mmrlさん、いつもどうもありがとうございます。ここから：

---

ちょっと計算してみましたのでご報告。

やったことは、matchingとmaximizing(強化学習、Optimization)で得られる解が違うのかどうかをSugrueらの離散時間型のVI-VIスケジュールで確認しました。

結論を先に言うとVI-VIの場合、

1. maximizingの解はmatchingの解に一致する
2. このときの各expected value for choiceは等しい

の２点です。

maximizationでは違う解が得られるのではないかと期待していたのですが、一致してかつuchidaさんが数行で計算した結果をいろいろいじくって確認しただけとなりました。また、簡単のため選択変更後遅延(change over delay, COD)はこの計算では用いていません。

7月1日に計算したように、n 回あるchoice Aを選択しなければ、そこに報酬が存在する確率は、

と表されます。ここで、は１回に報酬が降ってくる確率。

今、確率的に行動選択するとして、A を選択する確率とすると、まったくランダムに選択したとするとそのinter choice interval の分布は

このとき、expected value for choice A, はchoice probabiltiy の関数になって、

となります。同様に

これは、を下げれば下げるほどを上げることになります。

一方、income の方は

となりますからを下げれば0に漸近、1に近づければに漸近します。

maximization では、ある選択確率 のときの単位時間当たりの総報酬を最大化するわけですから、

が最大になるように、を見つければよいので微分して0に持っていけばよい。

ここで、となることに注意すると

において から によって最適解が与えられる。 すなわち均衡解というわけです。

さて、これで得られる解が

fractional income

のどのような関数になっているかというと とから

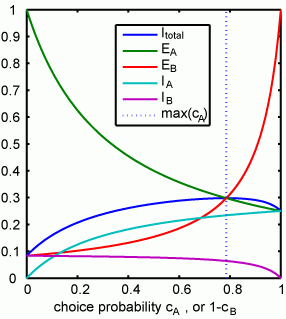
すなわちAのfractional incomeはAのchoice probability に一致する。つまりmatchingというわけです。あーつまんない計算だった。

休み２日掛けて考えたのに結局ＶＩＶＩはmatching とmaximizingが一致するように巧妙に仕組まれたタスクということだけがわかりました。

これって実はBaum 1981, Heyman 1979, Staddon Motheral 1978に書かれていたいりして...、調べてから計算しよう。ああ、無駄してしまった。

7月1日に書いたことも実はmomentary maximization theory (瞬時最大化理論)と呼ばれるものと同一だったりすることを[メイザーの学習と行動」を読み返して気づいてみたり...。無駄ばっかり。

---

ここまでです。編集過程で間違いが混入していたらお知らせください。

いやいや､無駄ではないですよ。手を動かした人がいちばん問題を理解した人になると思いますし。

メールにも書きましたが､generalizedでないMatching lawが成り立つためにはchange over delayの導入とVI-VI concurrentであることとが必須であるという理解だったのですが、今回の計算からするとchange over delay自体はalternating choiceのstrategyを排除するためだけに必要で、そんなにエッセンシャルなものではないのかもしれませんね。

しかしここまでくるとchange over delayとtauを組み込んだときにmaximizationとmatchingとの解がどのくらいずれるかということも検証できてしまいそうですね。それについては将来の著者たちの研究を待つか､ガッツのある方の参入を期待するということで､まずはmmrlさん、ありがとうございました。