[月別過去ログ] 2017年08月
« 2017年07月 | 最新のページに戻る | 2017年09月 »2017年08月24日
■ 「よくわかるフリストンの自由エネルギー原理」作成しました
スライド「よくわかるフリストンの自由エネルギー原理」を作成してslideshareにアップロードしました。
このスライドは栢森情報科学振興財団 第17回 Kフォーラム2017での発表をもとにして作成しました。そのときのスライドの構成は「1) 盲視についての吉田の研究の紹介 2) 自由エネルギー原理についての直感的な説明 3) 自由エネルギー原理を意識の理論にするためには」という3パートからなっていて、今回のスライドは2)の部分に該当します。3)についてもそのうち発表したい。
このスライドは以前作成したスライド「アクティブビジョンと フリストン自由エネルギー原理」の更新版と捉えていただけるとよいかと思います。以前のスライドについてはブログ記事(「セミナー「アクティブビジョンと フリストン自由エネルギー原理」スライドをアップロードしました」)にさらに情報があります。その当時は自由エネルギーの式をさらに簡略してあって、それだけ見てもどう自由エネルギーが計算できるかわからなかったのですが、今回は単純なケースではあるけれども、実際に自由エネルギーの値を計算しています。
FEPを正確に理解するためには機械学習(変分ベイズ)、そしてニューラルネットワーク(確率的勾配降下法)についての知識が必要となります。しかしそもそもそこまでしてFEPを理解する意義があるか、判断の材料を提供するために、神経科学者、心理学者、哲学者に向けてFEPの最小限の理屈を説明したい、というのが本スライドを作成した動機であります。そういうわけで、この説明では(世界一)単純化した例を用いているということを承知しておいていただきたい。
私自身はFEPをどのくらい重要だと思っているかというと、批判的に継承したいと考えていて、Kフォーラムでは3)の部分でその話をしました。そのうちそちらもまとめる予定。
2017年08月06日
■ 最尤法、MAP法、ベイズ推定についてのまとめ
ずいぶんと昔の話なのだけど、「比率のデータにエラーバーを付けたいんだけど」っていう記事を作ったときに、最尤法でも尤度関数の分布を使ってエラーバー(ベイズ的なcredible interval)を付けることができるよね、というのをやったことがある。そのときどうもしっくりきてなかったことを整理してみる。
最尤法の具体例として(この例自体は今回の話に必須なわけではないが)、二項分布でコインの表裏を で表現するとして、n回のコイン投げデータ が確率モデル(二項分布)のパラメータ (コインの表が出る確率)の尤度関数 は
となる。最尤法ではこの尤度関数 の最大値となるパラメータ を推定する。
これはベイズの枠組みで言えば、無情報のprior を使って計算したposteriorの分布の最大値となるパラメータ を推定することと等価だ。
いっぽうでベイズ推定の場合には、尤度そのものを使うのではなくて、ベイズの定理からposteriorの分布を推定している。
もしここで点推定したければ、
となる。
こうしてみると、posteriorの分布を推論する(inference)ところと、そのあとパラメーター を点推定(estimate)するところを分けて整理できるなと思った。
さっそく作ってみた。
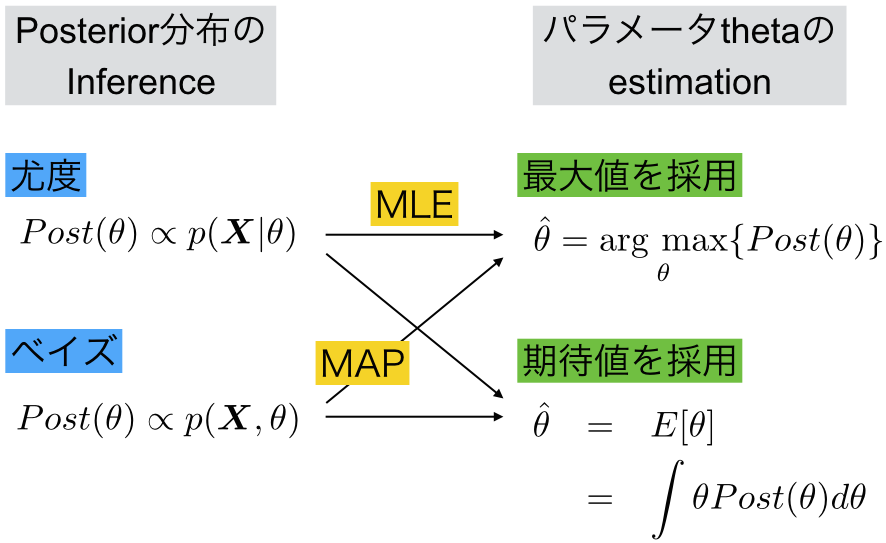
こんなかんじ。ベイズの定理に基づいてposteriorの分布を推論(infer)する方法に対して、priorの情報を使わない尤度を用いた方法がある。どちらもパラメーター の推測(estimate)を行う際には、最大値を採用する方法や期待値を採用する方法がある。
尤度関数の分布を求めた後に最大値を採用する方法が最大尤度法MLE(maximum likelihood estimation)であり、ベイズの公式でjoint probability (=generative model)の分布を求めた後に最大値を採用する方法がMAP法(maximum A posterior)だと。
つまり最大尤度法MLEという言葉を私が気持ち悪いなあと思ったのは、尤度関数を計算するところと、最大値を推定するところとが両方いっぺんに入っているからだということがわかった。「分布関数を計算する尤度推測(likelihood inference)」とそのあとの「最大値を採用する点推定MLE」みたいな言い方をするほうが混乱しなくていいんじゃないの?
なんか、MLEは点推定するけど、ベイズは点推定しないみたいな言い方はmisleadingだと思っていたので。
もちろんこれはベイズ史観であって、MLEを作ったフィッシャーの狙いとは異なるからこんな言い方はしないんだろうけど、そういった歴史的経緯以外にこの捉え方でまずいところってあるんだろうか?
でもってじつは本題は、このように整理すると、さらにhidden variable があるときのEMアルゴリズムと変分ベイズを並べることで2*2のマトリクスが作れるよって話だった。でもそこまで図を作る前に息切れしてしまった次第。
ところで、当たり前っちゃあ当たり前なんだけど、 も も も の関数であって、同じ一つのグラフの上に書ける。
それは当たり前のことなんだけど、式を字面だけ読んでいると、なんだか が の関数であるような(ぼんやりとした)勘違いをしてしることに気がついた。もちろん、べつに条件付き確率の左右にはどちらがgivenかといったそういう意味があるわけではない。
お勧めエントリ
- 細胞外電極はなにを見ているか(1) 20080727 (2) リニューアル版 20081107
- 総説 長期記憶の脳内メカニズム 20100909
- 駒場講義2013 「意識の科学的研究 - 盲視を起点に」20130626
- 駒場講義2012レジメ 意識と注意の脳内メカニズム(1) 注意 20121010 (2) 意識 20121011
- 視覚、注意、言語で3*2の背側、腹側経路説 20140119
- 脳科学辞典の項目書いた 「盲視」 20130407
- 脳科学辞典の項目書いた 「気づき」 20130228
- 脳科学辞典の項目書いた 「サリエンシー」 20121224
- 脳科学辞典の項目書いた 「マイクロサッケード」 20121227
- 盲視でおこる「なにかあるかんじ」 20110126
- DKL色空間についてまとめ 20090113
- 科学基礎論学会 秋の研究例会 ワークショップ「意識の神経科学と神経現象学」レジメ 20131102
- ギャラガー&ザハヴィ『現象学的な心』合評会レジメ 20130628
- Marrのrepresentationとprocessをベイトソン流に解釈する (1) 20100317 (2) 20100317
- 半側空間無視と同名半盲とは区別できるか?(1) 20080220 (2) 半側空間無視の原因部位は? 20080221
- MarrのVisionの最初と最後だけを読む 20071213