■ ダイエットから「行為する意識」執筆の話へ
ひさびさにウォーキングしてきた。書籍の執筆をはじめてから、ずっと運動せずに生活をしてきたのだけど、そろそろ健康的に危機感を感じたので、運動再開。やっぱ体を動かすと気分がいいな。
ダイエット歴の長い自分の持論なのだけど*、ダイエットしているときは心がさっぱりとしすぎて、執筆に専念するときのマインドセットには向いてない。
(* 「特技ダイエット、趣味リバウンド。いまのところ5勝6敗」といつも冗談めかして言ってるのだけど、もう正確な回数はわからなくなってる)
ダイエットをしているときは心がさっぱりしすぎて、「これで仕事終了、他のことに移ろう!」となる。それで自分のQOLは上がるけど、あとから見返してみれば、詰めの甘い、浅い仕事になる。
そうではなくて、「まだまだ足りない、これでは不十分なのではないか…」そういう心が粘り強く仕事を磨き上げると思ってる。そういうときの自分の方が好き。自分のQOLはよくないが。
「ダイエットすると心がさっぱりしすぎる」問題については20090121のブログ記事でも書いてた。
「ただメンタルな部分も健康になりすぎているかんじがする。なんかさっぱりしすぎてるというか、スクエアになってる。Twitterにポエム書いたりとかしないし。布団入ったらすぐ寝るし。ちょっと俺らしくない。わたしのクリエイティビティの源泉だとわたしが信じていたカオティックなというかそういったドロドロなものが後退してる。」
著書「行為する意識」についても、SNS上でのあの本へのコメントで「オートポイエーシス、エナクティビズム、自由エネルギー原理について、つまずきポイントを徹底して埋めてくれている」や「誤解の余地をいちいち潰してゆくスタイルがありがたい!」と書いてくれた部分はどれも、校了のギリギリまで粘って文章を磨いたところだった。
もし自分が効率厨であったなら、そんな労力をかけなくても、「書籍を出す」という見える実績さえ作ったら、あの本についてはさっさと心から手放して、別のプロジェクトを片付けるのがより生産的だったはずだ。
でもそんなやり方では俺の面白さが消えると思ってる。どうでもよいことにこだわっていると端からは見えるかもしれない。でも俺の俺らしい部分はそういうところにあって、もし違うやり方をしなければならないなら、それは俺がやる必要のない仕事だと思ってたりする。
執筆の舞台裏を書いておこう。(Xには書けないが、ブルスカは人がいないので書いてみた。それをまとめて、そっとブログにポストする。)
あとがきにも書いたけど、「行為する意識」は2021年11月から執筆を開始したものの、2022年くらいから2年間執筆がストップしている。それを再開したのが2024年12月のこと。
再開する前の段階(2024年12月18日)では、原稿はI-III章まで書き上げていた。(I章: NCC批判から予測的処理、II章: オートポイエーシスから生物学的自律性、III 好意的媒介から予測の概念へ)
中断の期間にほとんど心が折れかけていたのだけど、なんとか気を取り直した。再開の際には、残りIV章とV章を書き上げれば終了となるので、年末年始を全部使って書き上げることにした。
IV章に予測誤差とエナクティヴィズム、V章に神経回路学会の解説記事を加えて、最後まで原稿を書いたのが2025年1月14日。一ヶ月かかってない!
当然そのあいだ通常の業務はあったし、ウィンタースクールに参加して、研究会のプレゼンも作った。マヂ神の所業。
1月14日に書き上げたものでも、「予測誤差の概念でエナクティヴィズムを再解釈した本」くらいの体裁は整っていたはずだ。でもそれでは納得いく本にならないと思った。ここから3ヶ月かけて、原稿に大幅に加筆を行う作業が始まった。
この時点ではまだ、II章のオートポイエーシスの説明が紋切り型で、MaturanaとVarelaの違いにも言及してなかった。そこでII章はほぼ書き直しをすることにした。「オートポイエーシスとは操作的閉包と構造的カップリングである」という説明になるように大幅に書き換えて、さまざまな例も加えた。メトロノームの同期やホメオスタットのような力学系のシミュレーションまで加えることにした。
IV章に「予測誤差とエナクティヴィズム」を詰め込むのも無理な話で、2つの章に分けることにした。これによって新IV章は「予測を見直す」というテーマが明確になった。(「よい制御器定理」「大腸菌の予測」「アロスタシス」を入れてお膳立てしたうえで、予測誤差と自由エネルギー原理FEPを入れるという構成が確立した。)
新IV章の内容については、当初は予測誤差だけで限定して、FEPについて最小限の言及(「予測の束の調整」)だけの予定だったのだが、新V章で渡辺慧とベイズ力学に言及するために、能動的推論についての説明を入れることにした。(これで260ページだった本が350ページになったomg)
新V章でエナクティヴィズムのあとにふたたび予測誤差とFEPを再解釈する構成にした。これで「予測誤差を消費」というパンチラインを操作的閉包とつなげて、認知する我々の生物学的自律性を構成するものとする部分が完成した。
旧IV章を新IV章と新V章に分割して作り直したのが2025年3月7日。もう2度目の校正の段階なんだけど、「てにをは」じゃなくて、まだ論旨が変わるレベルで大きな変更加えてた。
新VI章(旧V章)で脳の過程と意識の過程の絡み合いと神経回路学会の解説記事(アクティブ・ヴィジョン)とを繋ぐために、ヴァレラの神経現象学を入れればよいということに気づいた。(どういうわけだか、この時点までヴァレラの神経現象学に言及してないことに気づいてなかった。) これによって「アクティブ・ヴィジョンの理論」も「吉田と田口の神経現象学」になった。これも3月。
新VI章で脳の過程と意識の過程の絡み合い(行為的媒介)について、状態と過程を深堀りすることで、これがヴァレラの神経現象学での「相互に拘束」を刷新するものだと気づいたのが4月6日。
そんなわけで、マヂでギリギリまで直してた。けっきょく校了したのが4月30日で、書籍の出版が5月26日。ほんと、執筆再開して5ヶ月で出版までたどり着いたのマヂ奇跡。
1月以降のこれらの追加によって、本書が全体的に難しくなってしまったことは認める。しかしもしこれらの追加をしていなければ、この本の内容は2018年の神経回路学会の解説記事からほとんど進歩しないものとなっていただろう。
もしあと1ヶ月時間があれば、第V章2後半の神経回路学会の解説記事を元にして書いた部分(アクティブ・ヴィジョンの神経現象学)を刷新することができたのに、と思う。そこに至るまでの部分を大幅にアップデートしたので、2018年に書いたこの部分は、もっと原型を留めないくらいに書き直しができたはずだ。その部分は悔やまれる。
(表現の正確さを期すならば、この部分の内容はだいぶ書き換えたので、校了の時点で納得行っている。今見直しても、ちゃんと完成していると思う。それでももし、校了直前のあのテンションをもう一ヶ月保つことができたら、この部分を刷新するアイデアが出たのでは、と思う。いつも火事場の馬鹿力で仕事をしているので、こうなりがち。)
そういうわけで、ダイエット談義に絡めたテイで、著書「行為する意識」の執筆時のエピソードを書いてみた。正直なところ、いま書いておかないと、自分でも忘れてしまうので。
- / ツイートする
- / 投稿日: 2025年07月12日
- / カテゴリー: [吉田+田口「行為する意識: エナクティヴィズム入門」]
- / Edit(管理者用)
■ ホメオスタット(homeostat)の挙動を再現してみる
前置き
このブログ記事は著書「行為する意識: エナクティヴィズム入門」のサポート資料として作成された。しかし、この本を読まなくても意味が通るようにこの記事は書かれている。
Matlabのコードは吉田のgithub (pooneil68/homeostat)に置いてある。式やコードの作成ではGemini 2.0の助けを借りたが、自分の目で確認を取った。
本文
精神科医でありサイバネティクスの先駆者であったウィリアム・ロス・アシュビーは、ホメオスタシスを電気回路で実現した「ホメオスタット」という機械を作り上げた(1940年代)。
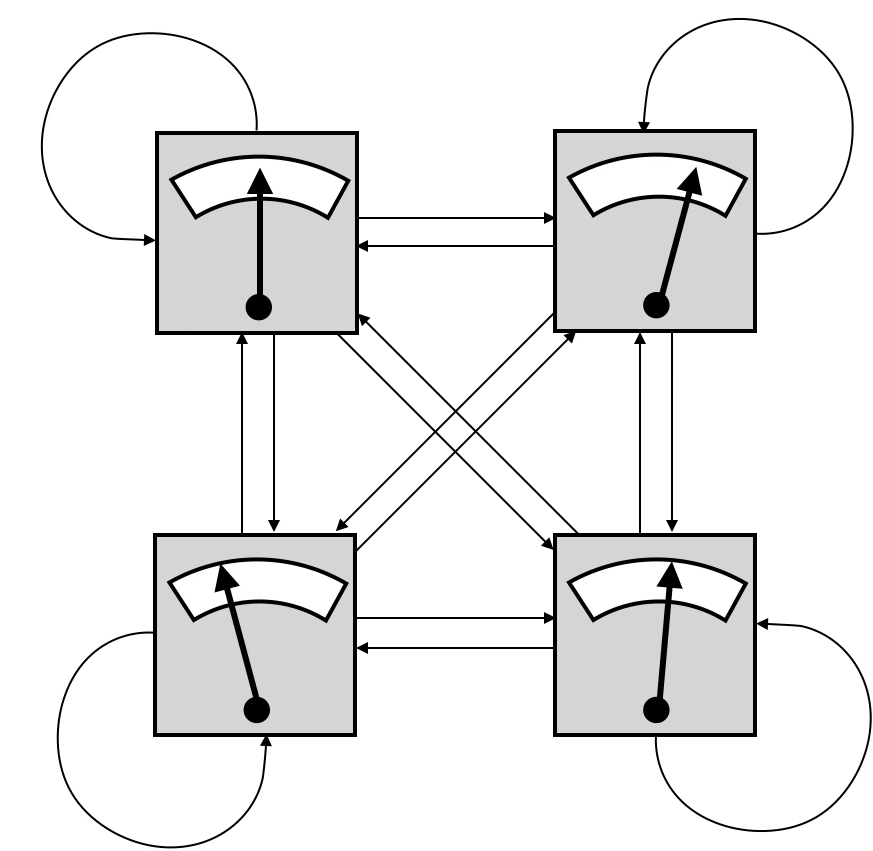
図1: ホメオスタットの構成
「ホメオスタットは四つのユニットから構成されている(図1)。それぞれが他の三つのユニットからの入力(と自分からのネガティブ・フィードバック入力)を受けて、これらの入力の重み付き合計が出力となる。この出力値が針で表示されている。それぞれの入力の重みと出力を調節できるようになっている。
この重みの調整がうまく行かないと、針は振り切れてしまう。しかし重みをうまく調整すると、すべての針の位置が中心に来て(適正値を指す)、システムが安定な状態を維持できる。しかもこの安定性はいったん成立すれば、どれか一つの出力を多少いじったとしても四つの針は適正な値のままでありつづける。このような自己修復性のことをアシュビーは超安定性(ultra-stability)と呼んだ。」(本書 p.63-64)
これは現在の視点からは、4つのユニットが全結合しているボルツマンマシンと同じ構造であると言える。しかしホメオスタットはボルツマンマシンと異なり、学習則を持っていない。このためホメオスタットは、安定でない状態になると重みをランダム化する操作を繰り返して、超安定性を確立できるまでその操作を繰り返す。それはまるで現在のスマホゲーでの「リセマラ」と同じ作業だ。
ホメオスタットの定式化
このブログ記事では、ホメオスタットの挙動を再現してみる。(参考文献は最後尾にあり)
ユニット $1,2,3,4$ それぞれの出力を $x_1(t), x_2(t), x_3(t), x_4(t)$ とする。このときそれぞれの出力は以下の微分方程式に従う。
$$ \begin{aligned} \frac{d^2 x_1(t)}{dt^2} &= h(a_{11} x_1(t) + a_{12} x_2(t) + a_{13} x_3(t) + a_{14} x_4(t)) - j \frac{d x_1(t)}{dt}\\ \frac{d^2 x_2(t)}{dt^2} &= h(a_{21} x_1(t) + a_{22} x_2(t) + a_{23} x_3(t) + a_{24} x_4(t)) - j \frac{d x_2(t)}{dt}\\ \frac{d^2 x_3(t)}{dt^2} &= h(a_{31} x_1(t) + a_{32} x_2(t) + a_{33} x_3(t) + a_{34} x_4(t)) - j \frac{d x_3(t)}{dt}\\ \frac{d^2 x_4(t)}{dt^2} &= h(a_{41} x_1(t) + a_{42} x_2(t) + a_{43} x_3(t) + a_{44} x_4(t)) - j \frac{d x_4(t)}{dt} &\qquad(1) \end{aligned} $$
ここで、$a_{11}, a_{12},...$ はそれぞれのユニット間の重みを表す。たとえば $a_{12}$ ならユニット$2$ からユニット$1$ への重みを表す。つまり右辺の第一項は、自分と他のユニットのすべての出力を重みを付けて足し合わせた入力を表している。
$h$ はこのような入力の評価を表す。ここでは定数で $1$ とする。(現在の人工ニューラルネットワークでは、$h$ の部分は活性化関数に該当する。活性化関数はReLUのように非線形性があるのだが、ホメオスタットでは線形和になっている。)
$j$ の入った項は、出力を示す針の粘性を反映している。ホメオスタットの針は水の上に浮かんでいて、入力に比例した磁石に反応して動く。このようなハードウェア的側面が考慮されている。ここでは定数で $0.5$ とする。
ホメオスタットの挙動
このように微分方程式で表現することができれば、初期値さえ決定してやればその挙動を図示することができる。ここでは微分方程式の数値計算のためにmatlabのode45関数を用いている(4次のルンゲ・クッタ法)。githubにある homeostat4.m を動かすと以下の図ができる。
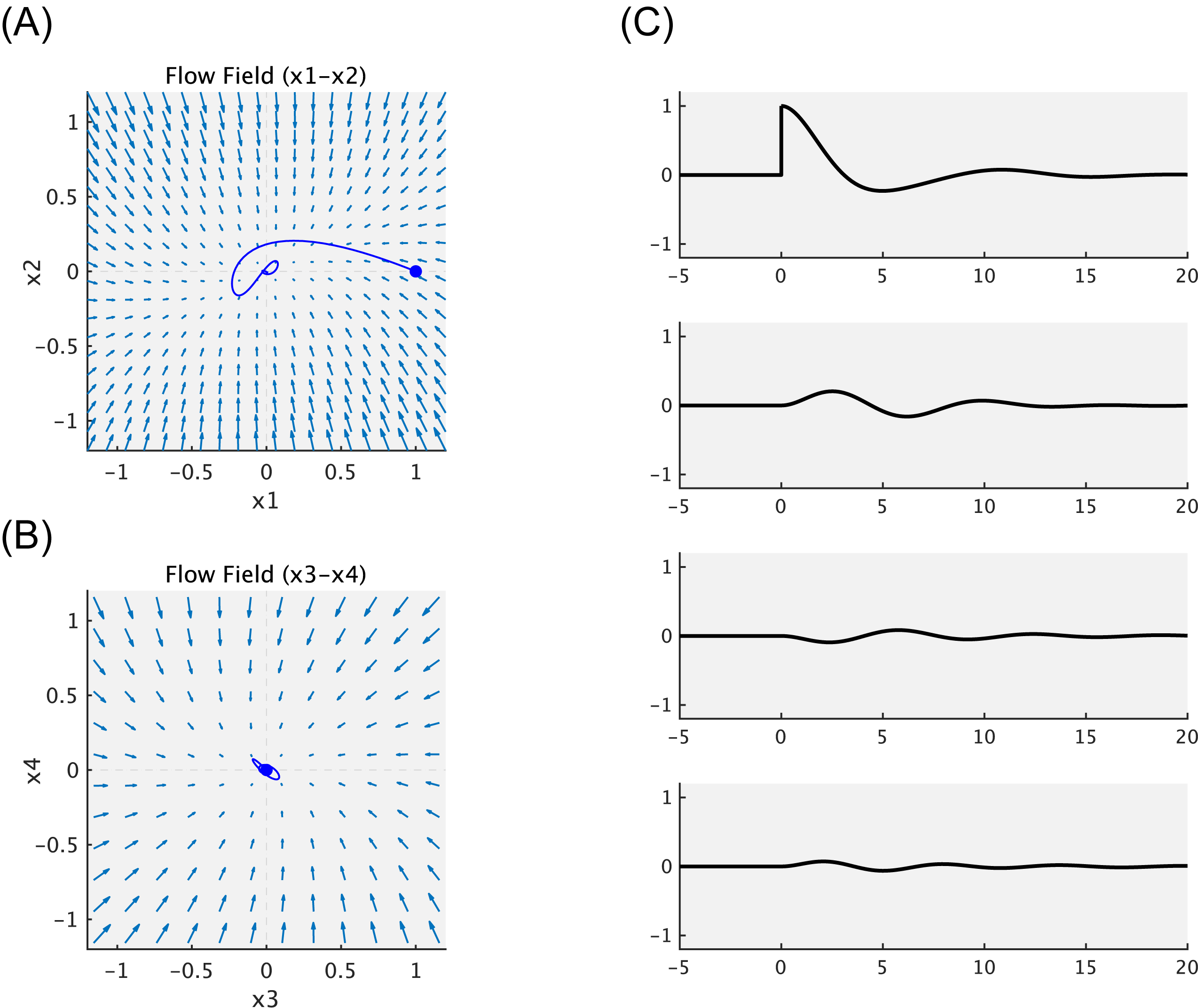
図2: ホメオスタットの挙動
まず図2の左側(A,B)はflow fieldを表している。これはネットワークの重み $a_{ji}$ と定数 $h,j$ によって決まる。Flow fieldは実際には4次元だが、ここでは $x_1 - x_2$ と $x_3 - x_4$ の2つの平面についてだけ表示してある。Flow fieldを見るだけで、初期値をどこにおいても、$0$ に収束することが予想つく。
じっさいにユニット1-4について初期値 $[0,0,0,0]$ を設定すると、ホメオスタットの出力は $[0,0,0,0]$ のまま変動しない。(図2(C)の横軸-5-0(秒)の部分。)
そこで時点 $0$ のところでホメオスタットのユニット1の出力を強制的に $1$ に変更してやる。するとユニット1は速やかに出力値が $0$ へと戻る。このときユニット2,3,4の出力も多少揺れているのがわかる。このようにして、このホメオスタットでは超安定性を達成できているいることがわかる。
ふたたび図2(A),(B)に戻ると、時点 $0$ のところでユニット1の出力を強制的に $1$ に変更したことが青丸で示してある。出力値は $0$ へと戻ってゆくのだが、それは一直線ではない。Flow fieldの向きに従って、多少揺れながら戻っている。
本書では図2を参照しながら「たとえばドカ食いをして血糖値スパイクがおきた状態(ユニット1)でも、健康であるならば、ただちに適正な生理状態が回復できることを示している。」(p.65-66)と書いている。お察しのとおり、この文章は「ドカ食いダイスキ! もちづきさん」を想定していた。初稿は「たとえばドカ食いをして「至った」状態でも」と書いたのだが、後年通じなくなるなと思って、文章を変えたのだった。
ホメオスタットの安定条件
ここで示した例ではホメオスタットは超安定性を達成できている。これはあらかじめそのような重みを選んでいたからだ。この安定条件を見つけるためには、ここまで書いたような、数値解析によって微分方程式の挙動を調べる方法では足りない。解析的な手法が必要となる。
ホメオスタットを定式化した $(1)$ は連立微分方程式になっているので、解析的に解くことができる。それによってどういう重みのときに超安定が達成できるかを調べることができる。
まず、連立方程式 $(1)$ を行列表現に書き換える。
$$ \begin{aligned} \frac{d^2}{dt^2} \begin{bmatrix} x_1(t) \\ x_2(t) \\ x_3(t) \\ x_4(t) \end{bmatrix} &= h \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix} \begin{bmatrix} x_1(t) \\ x_2(t) \\ x_3(t) \\ x_4(t) \end{bmatrix} -j\frac{d}{dt} \begin{bmatrix} x_1(t) \\ x_2(t) \\ x_3(t) \\ x_4(t) \end{bmatrix} \end{aligned} $$
ここで、$x=\begin{bmatrix}x_1(t) & x_2(t) & x_3(t) & x_4(t)\end{bmatrix}^{tr}$ 、 $x' = \frac{d}{dt}x$ 、 $x'' = \frac{d^2}{dt^2}x$
$$ \begin{aligned} A &= h \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix} \end{aligned} $$
とすると以下のように整理できる。
$$ \begin{aligned} x'' & = A x - j x' \end{aligned} $$
同次微分方程式 $x'' + jx' - Ax = 0$ を解くために、$x = v e^{st}$ の形の解を仮定する。ここで $v$ は定数ベクトル、$s$ は複素数のベクトル。
$x'' + jx' - Ax = 0$ に $x = v e^{st}$ を代入すると、
$$ \begin{aligned} &s^2 v e^{st} + j s v e^{st} - A v e^{st} = 0\\ &(s^2I + jsI - A) v e^{st} = 0\\ &s^2 I + jsI - A = 0 \end{aligned} $$
ここで $I$ は単位行列。この式が非自明な解を持つためには、行列式がゼロでなければならない。
$$ \begin{aligned} det(s^2 I + jsI - A) &= 0 \end{aligned} $$
これが特性方程式。この特性方程式の解 $s$ (複素数)の実部がすべて負であるときに収束する。こうしてホメオスタットがどういうときに超安定(収束)を確立し、どういうときに発散するかが計算できる。
しかしこの計算は4つのユニットの場合でさえ非常に複雑であるので、上記のコードではGeminiに安定条件を出してもらって、それを重み $A = {a_{ji}}$ に採用している。
ホメオスタットのその後
「ホメオスタットの挙動を見るかぎり、これは単なる生体恒常性(ホメオスタシス)のモデルに見えるかもしれない。しかしアシュビーはこれを著書『頭脳への設計』において「考える機械」のプロトタイプとして喧伝した。つまりアシュビーにとって、人工の脳をデザインするとは、チューリングマシンのような入力、出力、その変換関数で決まる制御システムを作ることよりはむしろ、外部からの擾乱に「能動的に」抵抗してそのシステムの状態を保つ側面のほうが重要だったようだ。」(本書p.66)
「アシュビーはその後ホメオスタットの大型化を目指したが、安定性を確立させることができなかった。現在の知識から言えば、うまくいかなかった理由は力学系の理論から明らかだった。というのもホメオスタットのユニットは入力の線形和によって駆動される、線形なシステムだったからだ。」(本書p.67)
本書ではこのように書いたのだが、その意味はこのブログ記事の説明からだいぶ明らかになっただろう。超安定性を確立するとは、特性方程式の安定解を見つけることだ。4つのユニットであれば、重みのランダム化(リセットマラソン)でそのような重みを見つけることはできたかもしれない。ユニット数を増やしたらランダムサーチという方法が立ち行かなくなることがわかる。
アシュビーはホメオスタットをスケールアップすることで、考える機械を作ることを目指していたのだが、このプロジェクトは成功しなかった。ではホメオスタットは無駄な試みだったのかというと、そんなことはない。ウィーナーによる評価、ディパオロたちによる再評価、このあたりについては本書をぜひ読んでみてほしい。
参考文献
- William Ross Ashby (1952) Design for a Brain, Chapman & Hall. (邦訳:『頭脳への設計―知性と生命の起源』山田坂仁ほか訳、宇野書店、1967年)
- Franchi S. (2013) Homeostats for the 21st century? Simulating Ashby simulating the brain. Constructivist Foundations 9(1): 93–101. http://constructivist.info/9/1/093
- Battle, S. (2015). Ashby’s Mobile Homeostat. In: Headleand, C., Teahan, W., Ap Cenydd, L. (eds) Artificial Life and Intelligent Agents. ALIA 2014. Communications in Computer and Information Science, vol 519. Springer, Cham. https://doi.org/10.1007/978-3-319-18084-7_9
- / ツイートする
- / 投稿日: 2025年06月07日
- / カテゴリー: [吉田+田口「行為する意識: エナクティヴィズム入門」]
- / Edit(管理者用)
■ 書籍「行為する意識: エナクティヴィズム入門」著者の対談動画をYoutubeに掲載しました
著者の吉田正俊と田口茂による対談動画をYoutubeに掲載しました。この本についての補足事項や、執筆風に考えたことなど、ざっくばらんに話をしています。(1)-(3)まであって、トータル100分弱です。
(1) 行為的媒介とは何か。関係一元論ではない。差異はなくならない。消費し切ることはできない。生きているものが持ち続ける不安定性(precaliousness)。循環的な意識の捉え方。因果的な説明の図式から、並行してプロセスが続く図式へ。AI時代でそれはより必要になる。
(2) 弱い因果のつながり。ビリヤードボールの連鎖から、メトロノームの同期へ。関係性のネットワーク重視による相対主義の闇へ。「現実は幻である」というのは関係一元論の帰結。エナクティヴィズムでの「自分で自分の価値を作る」という考え。でもエナクティヴィズムはオルタナティブではない。今後メインストリームに入ってくる話であり、現在のAIに貢献しうる考えである。本書執筆の経緯。予測誤差消費理論ができるまで。オートポイエーシスの脱神秘化。
(3) 将来の課題。状態と過程。アクティブ・ヴィジョンについての掘り下げ。潜在性の掘り下げ。観察的媒介でない形での意識の解明。意識の科学の進歩によって科学が変わる。GNWTとIITの敵対的協力論文。ニセ科学レター。ベンジャミン・リベットの運動準備電位。運動についても自分に揺らぎを作りながら、生物の自律性に根付いた、運動を生成している。ここに「生命の自由」ができる。AI/LLMはなぜうまくいっているか。「当たってる感」とはいったいなにか。
以上です。
- / ツイートする
- / 投稿日: 2025年05月22日
- / カテゴリー: [吉田+田口「行為する意識: エナクティヴィズム入門」]
- / Edit(管理者用)
■ パレイドリアと「シミュラクラ現象」
大学で意識についての講義をするときに、いろいろ錯覚を見てもらったりするのだけど、そこでの質問やコメントに「シミュラクラ現象」という言葉が出てくることがある。
認知心理学の分野ではパレイドリアPareidoliaという言葉があって、「壁のシミが人の顔のように見えてしまう」という現象をパレイドリアと呼ぶ。「シミュラクラ現象」というのが指しているのは、典型的には「コンセントの3つの穴が人の顔のように見える」というもので、これはパレイドリアの一種であり、わざわざ「シミュラクラ現象」という言葉を使う必要がない。
そもそも「シミュラクラ現象」という言葉は日本でしか通用しない言葉だ。それはwikipediaの「シミュラクラ現象」の項目を見ればわかる。日本語版しか無い。
そういうわけで、講義で学生から「シミュラクラ現象」についてのコメントをもらった場合には「それは学問的にはパレイドリアと呼ばれるものであって、「シミュラクラ現象」という言葉は日本のネットカルチャーでのみ通用する言葉なのでお気をつけください。」と返事するようにしている。
言葉は生き物なのだから「シミュラクラ現象」という言葉自体を禁止してもしょうがない。だから、ネットに向かって「「シミュラクラ現象」という言葉は誤用です。使うのはやめましょう」とか喧伝しようとは自分は思わない。
とはいえ、「シミュラクラ現象」という言葉のルーツは抑えておきたい。初出はいつかLLMに聞いてみたら、「初出を見つけるのは難しいけど、初期の使用例については2000-2005年の範囲でググってみましょう」とアドバイスされた。
すると2005年の記事が二つ見つかった。
それは「シミュラクラ現象(類像現象)」かもしれません。シミュラクラ現象とは3つの点が集まった図形が人間の顔のように見えるという錯覚現象です。ほら、よくマンホールのフタの模様や、天井のシミが人の顔のように見えてくることがありますよね。もともとはSF作家・フィリップ・K・ディックの小説から生まれた言葉だそうで。
「こうゆうもののコトを「シミュラクラ」と呼ぶ。●が三角に3つ並べば顔に見えるとまで言われる。人間にはあらゆるものを顔に見立ててしまう本能が備わっているらしい。(…)何を言いたいかっちゅーと、心霊写真と言われるもののすべて、とまで言うつもりはないが、9割方はこの「シミュラクラ」だとおれは思っているのだ。」
どちらとも心霊写真の文脈で、それは錯覚だ、シミュラクラ現象で説明できる、というものだ。ここでひとつ興味深いことが書かれている。
もともとはSF作家・フィリップ・K・ディックの小説から生まれた言葉
元々シミュラクラSimulacreという言葉は、ポストモダンの哲学者ジャン・ボードリヤールによる「シミュラークルとシミュレーション」から来ている。(BTの記事の解説がわかりやすかった)
そしてそれの影響を受けて、フィリップ・K・ディックはSF作品として「シミュラクラ」という作品を書いている。私は未読だが、人間そっくりに作られたシミュラクラが出てくる話だそうだ。
というわけで、「シミュラクラ現象」という言葉がオカルトとか心霊写真とかのサブカルチャーの文脈で出てきたことを考えると、はじめてこの言葉を使った人は、ボードリヤールを引用したというよりは、フィリップ・K・ディックを引用したのではないかと想像できる。
さて、認知心理学の分野でパレイドリアの専門家といえばまっさきに浮かぶのは高橋康介さんだ。彼は「なぜ壁のシミが顔に見えるのか ―パレイドリアとアニマシーの認知心理学―」 という本を書いている。
Twitter(当時)だと、以下のスレッドが詳しい。
パレイドリアの話をすると「それシミュラクラでは?」という反応がよくあります。wikipediaの力だろうか。それともPKディックのこれ? https://amazon.co.jp/dp/B077QN78N1/ 必要に迫られてパレイドリアとシミュラクラの語源についてかなり調べたことがあるんですが、結局正確なところはわかりませんでした。Twitter 2020
上述の書籍の中でも、「シミュラクラ現象」について手短に触れている。
パレイドリアとシミュラクラはともに同じような概念を示すものだが、パレイドリアが見えてしまう「現象」を示すのに対して、シミュラクラは見えてしまう現象のきっかけとなる「モノ」を指し示す意味合いが強い。…「シミュラクラ現象」といえば、それはパレイドリアとほぼ同義であると思ってよいだろう。(p.46)
ということで、「シミュラクラ現象」という言葉をむやみに切り捨てることなく、考察している。(とはいえこの本で「シミュラクラ現象」が出てくるのは、あくまでもこの部分だけにすぎない。)
というわけで、今後は質問をもらったら、この記事を参照できるようにした。
■ 書籍「行為する意識: エナクティヴィズム入門」の文献リスト(英語論文、日本語論文、英語書籍)
本書での文献引用は、該当ページ(もしくはそれより後ろの図のないページ)の左側に表記してあります。日本語書籍については本書巻末の「主要参考文献」にリストを作成してあります。英語論文、日本語論文、英語書籍については、こちらにリストを作成しました。登場順となっております。)
文献リスト
(日本語書籍については本書巻末の「主要参考文献」にリストあり。こちらでは、英語論文、日本語論文、英語書籍について、登場順でリストを作成した。)
I章
- Crick F and Koch C (1990) Towards a neurobiological theory of consciousness. Seminars. Neuroscience 2: p. 263-75.
- Quiroga, R., Reddy, L., Kreiman, G., Koch, C., & Fried, I. (2005) Invariant visual representation by single neurons in the human brain. Nature, 435 (7045), p. 1102-7.
- Kreiman G, Fried I, Koch C. (2002) Single-neuron correlates of subjective vision in the human medial temporal lobe, Proc Natl Acad Sci U S A. 99(12), p. 8378-83.
- Parvizi J, Jacques C, Foster BL, Witthoft N, Rangarajan V, Weiner KS, Grill-Spector K (2012) Electrical stimulation of human fusiform face-selective regions distorts face perception, J Neurosci. 32(43), p. 14915-20.
- Schalk G et al (2017) Facephenes and rainbows: Causal evidence for functional and anatomical specificity of face and color processing in the human brain, Proc Natl Acad Sci U S A. 114(46), p. 12285-90.
- Albantakis L, Tononi G (2014) From the Phenomenology to the Mechanisms of Consciousness: Integrated Information Theory 3.0. PLoS Comput Biol 10(5): e1003588.
- Tsuchiya N, Taguchi S, Saigo H. (2016) Using category theory to assess the relationship between consciousness and integrated information theory. Neurosci Res. 107:1-7.
- Marr, D. (1982). Vision: A Computational Investigation into the Human Representation and Processing of Visual Information. New York, NY: W. H. Freeman & Company.(邦訳:『ビジョン―視覚の計算理論と脳内表現』乾敏郎+安藤広志訳、産業図書、1987年)
- Komatsu H, Kinoshita M, Murakami I. (2000) Neural responses in the retinotopic representation of the blind spot in the macaque V1 to stimuli for perceptual filling-in. J Neurosci. 20(24): p. 9310-9.
- Komatsu H. (2006) The neural mechanisms of perceptual filling-in, Nat Rev Neurosci. 7(3): p. 220-31.
- Kolers PA, von Grünau M. (1976) Shape and color in apparent motion, Vision Res. 16(4): p. 329-35.
- Henderson JM, Hollingworth A. (2003) Global transsaccadic change blindness during scene perception, Psychol Sci. 14(5): p. 493-7.
- Edwards HM, Jackson JG and Evans H (2022) Neuroticism as a covariate of cognitive task performance in individuals with tinnitus. Front. Psychol. 13:906476.
- Hermann von Helmholtz (1867). Handbuch der physiologischen Optik. Leibzig: Leopold Voss
- Blakemore SJ, Wolpert D, Frith C. (2000) Why can’t you tickle yourself? Neuroreport. 11(11): R11-6.
- Andy Clark (2016) Surfing Uncertainty, Oxford: Oxford University Press
- Roy M. Pritchard (1961) Stabilized Images on the Retina. Scientific American, 204(6), p. 72-9
II章
- William Ross Ashby (1952) Design for a Brain, Chapman & Hall.(邦訳:『頭脳への設計―知性と生命の起源』山田坂仁ほか訳、宇野書店、1967年)
- Andrew Pickering (2010) The Cybernetic Brain: Sketches of Another Future. University of Chicago Press
- R. C. Conant and W. R. Ashby. (1970) Every good regulator of a system must be a model of that system, Int. J. Systems Sci., vol 1, No 2, p. 89-97
- Barlow, H. B. (1961) Possible principles underlying the transformations of sensory messages, Sensory Communication, Ed. W. Rosenblith, Cambridge: MIT Press, Ch1, p. 217-34.
- Barlow, H. B. (1972) Single units and sensation: a neuron doctrine for perceptual psychology? Perception 1, p. 371-94.
- Barlow H. (2009) Grandmother cells, symmetry, and invariance: how the term arose and what the facts suggest, The Cognitive Neurosciences, 4th Edn, ed Michael Gazzaniga, Cambridge: MIT Press, p. 309-20.
- Eifuku S, De Souza WC, Tamura R, Nishijo H, Ono T. (2004) Neuronal correlates of face identification in the monkey anterior temporal cortical areas. J Neurophysiol. 91(1):358-71.
- Chang L, Tsao DY. (2017) The Code for Facial Identity in the Primate Brain. Cell. 169(6):1013-1028.e14.
- Waidmann EN, Koyano KW, Hong JJ, Russ BE, Leopold DA. (2022) Local features drive identity responses in macaque anterior face patches. Nat Commun. 13(1):5592.
- Friston K. (2013) Life as we know it, J R Soc Interface. 10(86)
- Bertschinger N., Olbrich E., Ay N., Jost J. (2006) Information and closure in systems theory, Explorations in the Complexity of Possible Life, Proceedings of the 7th German Workshop of Artificial Life, (Amsterdam) p. 9-21
- Di Paolo, E., & Thompson, E. (2014) The enactive approach. In L. Shapiro (Ed.), Routledge handbooks in philosophy. The Routledge handbook of embodied cognition (p. 68-78) Routledge.
- De Jaegher, H., Di Paolo, E., & Gallagher, S. (2010). Can social interaction constitute social cognition? Trends in Cognitive Sciences, 14(10), p. 441-7.
- Francisco J. Varela (1979) Principles of Biological Autonomy. The North-Holland Series in General Systems Research, Vol. 2. New York: Elsevier North-Holland, Inc.
- Froese T. & Stewart J. (2010) Life after Ashby: Ultrastability and the autopoietic foundations of biological individuality. Cybernetics & Human Knowing 17(4): 7-50.
- Varela, F. J. (1997) Patterns of life: intertwining identity and cognition, Brain and Cognition 34: p. 72-87.
- Varela, F. J. (1994) On defining life. In: G. Fleischeker and M. Colonna (eds), Self-reproduction of Supramolecular Structures, p. 23-33. Nato ASI Series, Plenum Press.
- Weber, A., Varela, F.J. (2002) Life after Kant: Natural purposes and the autopoietic foundations of biological individuality. Phenomenology and the Cognitive Sciences 1, p. 97-125.
- *Andrew Pickering (2010) The Cybernetic Brain. Sketches of Another Future. University of Chicago Press.
- Daniel C, Mason OJ. Predicting psychotic-like experiences during sensory deprivation. Biomed Res Int. 2015;2015:439379.
- Tsodyks, M., Kenet, T., Grinvald, A. and Arieli, A. (1999) Linking Spontaneous Activity of Single Cortical Neurons and the Underlying Functional Architecture, Science, 286, p. 1943-6.
- Durstewitz D, Koppe G, Thurm MI. (2023) Reconstructing computational system dynamics from neural data with recurrent neural networks. Nat Rev Neurosci, 24(11): p. 693-710.
- Warren S. McCulloch; Walter Pitts (1943) A logical calculus of the ideas immanent in nervous activity, Bulletin of mathematical Biology, 5(4): p. 115-33.
- A L Hodgkin and A F Huxley. (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve, J. Physiol, 117(4): p. 500-44.
- Izhikevich, E. M. (2007) Dynamical Systems in Neuroscience. MIT Press, Cambridge.
- Lara, A. H., Cunningham, J. P. & Churchland, M. M. (2018) Different population dynamics in the supplementary motor area and motor cortex during reaching, Nature Communications 9, 2754.
- Isomura, T. (2023) Bayesian mechanics of self-organising systems, arXiv preprint arXiv:2311.10216.
- 磯村拓哉(2025)「知能の統一理論への道標」『神経回路学会誌』32(1), p.47-57.
- 吉田正俊+田口茂(2018)「自由エネルギー原理と視覚的意識」『日本神経回路学会誌』25 (3), p. 53
III章
- Chalmers, D. J. (1995) Facing Up to the Problem of Consciousness, Journal of Consciousness Studies 2(3): p. 200-19.
- Husserl, E. (1984) Logische Untersuchungen, Band II/1, Husserliana XIX/1, Den Haag: Martinus Nijhoff.
- *田口茂(2022)「田辺元の「媒介」概念とそのポテンシャル」『危機の時代と田辺哲学』法政大学出版局、p. 97-116
- 田口茂(2024)「「媒介」概念の可能性―現代的コンテクストにおける田辺哲学」『日本哲学史研究』(20), p. 90-121
- Luhmann, N. (2013) Introduction to Systems Theory, Cambridge: Polity.
- Luhmann, N. (2002) Theories of Distinction, Stanford: Stanford UP.
- 田口茂+西郷甲矢人+大塚淳(2020)「現象学的明証論と統計学―経験の基本的構造を求めて」『哲学論叢』(47), p. 20-34
- 川岸郁朗+入枝泰樹+坂野聡美(2006)「大腸菌走化性シグナル伝達機構―タンパク質局在と相互作用を中心に」『物性研究』85(5), p. 668-84
IV章
- Tagkopoulos I, Liu YC, Tavazoie S. (2008) Predictive behavior within microbial genetic networks, Science, 320(5881): p. 1313-7.
- 大平英樹(2023)「内受容感覚・意思決定・感情の統合―予測的処理としてのアロスタシス」BRAIN and NERVE 75(11)1197-1205
- Sterling P, Eyer J. (1988) Allostasis: a new paradigm to explain arousal pathology. In: Fisher S, Reason J, editors. Handbook of Life Stress, Cognition and Health.
- Sterling P. (2012) Allostasis: a model of predictive regulation. Physiol Behav. 106(1), p. 5-15.
- Bechtel W, Bich L. (2024) Rediscovering Bernard and Cannon: Restoring the Broader Vision of Homeostasis Eclipsed by the Cyberneticists. Philosophy of Science. Published online 2024, p. 1-22.
- Friston K, Thornton C and Clark A (2012) Free-energy minimization and the dark-room problem. Front. Psychology 3:130.
- Barlow, H. B. (1961). Possible principles underlying the transformation of sensory messages. Sensory Communication, 1(01).
- Rao RP, Ballard DH. Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat Neurosci. 1999;2(1):79-87.
- Linxing Preston Jiang and Rajesh P. N. Rao (2022) Predictive Coding Theories of Cortical Function. In: Oxford Research Encyclopedia of Neuroscience, S. Murray Sherman (ed.)
- Friston, Karl (2005) A theory of cortical responses. Phil. Trans. R. Soc. B360815–836
- 吉田正俊+田口茂(2018)および吉田正俊+宮園健吾+西尾慶之+山下祐一+鈴木啓介(2023)「自由エネルギー原理、能動的視覚、サリエンス」『人工知能』38(6), p. 787-95
- Friston, K. (2010) The free-energy principle: a unified brain theory?. Nat Rev Neurosci 11, p. 127–38.
- Floegel M, Kasper J, Perrier P, Kell CA. (2023) How the conception of control influences our understanding of actions, Nat Rev Neurosci. (5), p. 313-29.
V章
- L R Squire, B J Knowlton (1994) The Cognitive Neurosciences, ed M Gazzinga, Cambridge: MIT Press.
- O’Regan JK, Noë A. (2001) A sensorimotor account of vision and visual consciousness. Behav Brain Sci. 24(5):939-73; discussion 973-1031.
- William James (1890) The Principles of Psychology.
- Egbert MD and Barandiaran XE (2014) Modeling habits as self-sustaining patterns of sensorimotor behavior. Front. Hum. Neurosci. 8: p. 590.
- Buhrmann T, Di Paolo EA and Barandiaran X (2013) A dynamical systems account of sensorimotor contingencies. Front. Psychol. 4: p. 85.
- Suzuki, K., Wakisaka, S. & Fujii, N. (2012) Substitutional Reality System: A Novel Experimental Platform for Experiencing Alternative Reality. Sci Rep 2, 459.
- Hurley, S., Noë, A. (2003) Neural Plasticity and Consciousness. Biology & Philosophy 18, p. 131-68.
- Wu et al (2024) Network state transitions during cortical development. Nat Rev Neurosci. 25(8), p. 535-52.
- Held R, Hein A. (1963) Movement-Produced Stimulation in the Development of Visually Guided Behavior. J Comp Physiol Psychol. 56, p. 872-6.
- Attinger A, Wang B, Keller GB. (2017) Visuomotor Coupling Shapes the Functional Development of Mouse Visual Cortex, Cell 169(7): 1291-302. e14.
- Barandiaran, X.E. (2017) Autonomy and Enactivism: Towards a Theory of Sensorimotor Autonomous Agency. Topoi 36, p. 409-30.
- 廣田隆造+西郷甲矢人+田口茂(2024) 「モノイドとしての自己―自律性への圏論的アプローチ」『人工知能学会全国大会論文集』第38回 4S1OS30a05-4S1OS30a05, 2024
- 廣田隆造「エナクティヴ・アプローチの現在―その原理と展開」『システムとサイバネティクスの思想/システム論』(コロナ社より出版予定)
- Di Paolo, E., & Thompson, E. (2014) The enactive approach. In L. Shapiro (Ed.), Routledge handbooks in philosophy. The Routledge handbook of embodied cognition (p. 68-78). Routledge.
- Kiernan et al (2011) Amyotrophic lateral sclerosis. Lancet. 377(9769), p. 942-55.
- Renart et al (2010) The asynchronous state in cortical circuits. Science. 327(5965), p. 587-90.
- Sohal VS, Rubenstein JLR. (2019) Excitation-inhibition balance as a framework for investigating mechanisms in neuropsychiatric disorders. Mol Psychiatry. 24(9), 1248-1257.
- Shahaf G, Marom S. (2001) Learning in networks of cortical neurons. J Neurosci, 21(22), 8782-8.
- A Masumori, T Ikegami, L Sinapayen (2019) Predictive Coding as Stimulus Avoidance, Spiking Neural Networks. 2019 IEEE Symposium Series on Computational Intelligence (SSCI), p. 271-7.
- N’Dri, A.W., Gebhardt, W., Teulière, C., Zeldenrust, F., Rao, R.P., Triesch, J., & Ororbia, A.G. (2024) Predictive Coding with Spiking Neural Networks: a Survey. arXiv:2409.05386
- Hertäg L, Sprekeler H. (2020) Learning prediction error neurons in a canonical interneuron circuit. eLife. 21; 9:e57541.
- Crick, F., Koch, C. (1998) Constraints on cortical and thalamic projections: the no-strong-loops hypothesis, Nature 391, p. 245-50.
- Collerton D, Tsuda I, Nara S. (2024) Episodic Visual Hallucinations, Inference and Free Energy. Entropy (Basel). 26(7), p. 557.
- 島崎秀昭(2019)「ベイズ統計と熱力学から見る生物の学習と認識のダイナミクス」『日本神経回路学会誌』26(3)、p. 72-98
- Adams RA, Shipp S, Friston KJ. (2013) Predictions not commands: active inference in the motor system. Brain Struct Funct. 218(3), p. 611-43.
- Allen M, Friston KJ. (2018) From cognitivism to autopoiesis: towards a computational framework for the embodied mind. Synthese. 195(6), p. 2459-82.
- Bruineberg, J., Kiverstein, J. & Rietveld, E. (2018) The anticipating brain is not a scientist: the free-energy principle from an ecological-enactive perspective. Synthese 195, 2417-44.
- Kirchhoff, M.D. (2018) Autopoiesis, free energy, and the life–mind continuity thesis. Synthese 195, 2519-40.
- Di Paolo, Thompson & Beer (2022) Laying down a forking path: Tensions between enaction and the free energy principle. Philosophy and the Mind Sciences, 3.
- Ramstead Maxwell J. D., Sakthivadivel Dalton A. R., Heins Conor, Koudahl Magnus, Millidge Beren, Da Costa Lancelot, Klein Brennan & Friston Karl J. (2023) On Bayesian mechanics: a physics of and by beliefs. Interface Focus. 1320220029
VI章
- Frank, A., Gleiser, M., Thompson, E. (2024) The Blind Spot: Why Science Cannot Ignore Human Experience. Cambridge: MIT Press.
- Merleau-Ponty, M. (1962). Phenomenology of Perception, trans. C. Smith, London: Routledge and Kegan Paul.
- Sartre, J.-P. (1943). L‘étre et le néant. Paris: Éditions Gallimard, p. 111, 116.(J・P・サルトル(2007)『存在と無』Ⅰ、松浪信三郎訳、ちくま学芸文庫、p. 228, 233)
- Sartre, Jean-Paul (1947). Une idée fondamentale de la phénomenologie de Husserl: L’intentionnalité, in : Situations I, Paris: Gallimard, p.33.(サルトル(1978)「フッサールの現象学の根本的理念―志向性」白井健三郎訳『シチュアシオンⅠ』人文書院、p. 28)
- Varela, F. J. (1996) Neurophenomenology: a methodological remedy for the hard problem. Journal of Consciousness Studies 3, p. 330-49.(邦訳:「神経現象学」『現代思想』vol.29-12、2001年10月号)
- Varela, F. J. (1999) The specious present: A neurophenomenology of time consciousness in Naturalizing phenomenology: Issues in Contemporary Phenomenology and Cognitive Science (Petitot, J., Varela, F. J., Pachoud, B. & Roy, J.-M.) p.266-329 (Stanford University Press). 邦訳:p. 196 (『現代思想』vol.29-12、2001年10月号)
- Lutz A, Lachaux JP, Martinerie J, Varela FJ. (2002) Guiding the study of brain dynamics by using first-person data: synchrony patterns correlate with ongoing conscious states during a simple visual task. Proc Natl Acad Sci U S A. 2002 Feb 5;99(3):1586-91.
- Le Van Quyen M. (2010). Neurodynamics and phenomenology in mutual enlightenment: The example of the epileptic aura. In Stewart J., Gapenne O., Di Paolo E. A. (Eds.), Enaction: Toward a new paradigm for cognitive science (p. 245–66). Cambridge, MA: The MIT Press.
- Petitmengin, C. Describing one’s subjective experience in the second person: An interview method for the science of consciousness. Phenom Cogn Sci 5, p. 229-69 (2006).
- Miyahara, K., Niikawa, T., Hamada, H. T., & Nishida, S. (2020). Developing a short-term phenomenological training program: A report of methodological lessons. New Ideas in Psychology, 58, Article 100780.
- Durstewitz D, Koppe G, Thurm MI. (2023) Reconstructing computational system dynamics from neural data with recurrent neural networks. Nat Rev Neurosci. 24(11):693-710.
- Favela, L.H. (2021) The dynamical renaissance in neuroscience. Synthese 199, 2103-2127.
- Froese T. (2023) Irruption Theory: A Novel Conceptualization of the Enactive Account of Motivated Activity. Entropy (Basel). 25(5):748.
- Thompson E, Varela FJ. (2001) Radical embodiment: neural dynamics and consciousness. Trends Cogn Sci. 5(10), p. 418-25.
- Husserl, E. (1972). Erfahrung und Urteil. Hamburg: Felix Meiner.
- Zahavi, D. (2005). Subjectivity and Selfhood. Cambridge MA: Bradford Book/ MIT Press.
- 田口茂(2015)「媒介論的現象学の構想」『ハイデガーフォーラム』Vol. 9, p. 37-48.
- Hohwy J, Roepstorff A, Friston K. (2008) Predictive coding explains binocular rivalry: an epistemological review. Cognition. 108(3) p. 687-701.
- Merleau-Ponty, M. (1945). Phénoménologie de la Perception. Paris: Gallimard.
- Di Paolo, E.A. (2000) Homeostatic adaptation to inversion in the visual field and other sensorimotor disruptions. In J. Meyer, A. Berthoz, D. Floreano, H. Roitblat, & S. Wilson (Eds.), From Animalsto Animats VI: Proceedings of the 6th International Conference on Simulation of Adaptive Behavior, p. 440-9. Cambridge: MIT Press.
- Iizuka H, Di Paolo EA. (2007) Toward Spinozist Robotics: Exploring the Minimal Dynamics of Behavioral Preference. Adaptive Behavior. 15(4): p. 359-76.
- Keramati M, Gutkin B. (2014) Homeostatic reinforcement learning for integrating reward collection and physiological stability. Elife. 2014 Dec 2;3:e04811.
- Yoshida N, Arikawa E, Kanazawa H, Kuniyoshi Y. (2014) Modeling long-term nutritional behaviors using deep homeostatic reinforcement learning. PNAS Nexus. 3(12): p. 540.
- Sass LA, Parnas J. (2003) Schizophrenia, consciousness, and the self. Schizophr Bull. 29(3): p. 427-44.
- Gallagher, S. (2000). Philosophical conceptions of the self: Implications for cognitive science, Trends in Cognitive Sciences, 4(1), p. 14-21.
- Howes, O. D. & Murray, R. M. (2014) Schizophrenia: an integrated sociodevelopmental-cognitive model. Lancet 383, p. 1677-87.
- Kapur S. (2003) Psychosis as a state of aberrant salience: a framework linking biology, phenomenology, and pharmacology in schizophrenia, Am J Psychiatry, 160(1), p. 13-23.
- MacDonald N. (1960) Living with schizophrenia. Can Med Assoc J. 82, p. 218-21.
- Kapur S. (2004) How antipsychotics become anti-“psychotic”--from dopamine to salience to psychosis. Trends Pharmacol Sci. 25(8): p. 402-6.
- 谷徹(2009)「現象学と間文化性」『現代思想』37(16), p. 131
- Varela F. & Depraz N. (2005). At the Source of Time: Valence and the Constitutional Dynamics of Affect. Journal of Consciousness Studies 12 (8): p. 61-81.
- 吉田正俊+宮園健吾+西尾慶之+山下祐一+鈴木啓介(2022)「サリエンスをアフォーダンスとして捉え直す―能動的推論の視点からの、精神病症状の異常サリエンス仮説への示唆」Jxiv doi:10.51094/jxiv.148
- ニクラス・ルーマン(2012)「社会システムのオートポイエーシス」『自己言及性について』(邦訳:大方透+大澤善信訳、ちくま学芸文庫、2016年、p. 7-39)
- Maturana H. R. (2012) Reflections on my collaboration with Francisco Varela. Constructivist Foundations 7(3): p. 155-64.
- Varela F. (1996) The early days of autopoiesis: Heinz and Chile, Systems Research, 13(3), p. 407-16.
- Hohwy J. (2016) The Self-evidencing brain, Noûs 50: p. 259–285.
- Gallagher S, Allen M. (2018) Active inference, enactivism and the hermeneutics of social cognition. Synthese. 195(6): 2627-2648.
- 中井久夫(2004)「世界における索引と徴候」『徴候・記憶・外傷』みすず書房
- Hasson U, Nastase SA, Goldstein A. (2020) Direct Fit to Nature: An Evolutionary Perspective on Biological and Artificial Neural Networks. Neuron. 105(3) p. 416-34.
- Tsuda, I., Yamaguti, Y., & Watanabe, H. (2016) Self-Organization with Constraints: A Mathematical Model for Functional Differentiation. Entropy, 18(3), p. 74.
補論
- Niikawa T, Miyahara K, Hamada HT, Nishida S. (2020) A new experimental phenomenological method to explore the subjective features of psychological phenomena: its application to binocular rivalry, Neurosci Conscious, 2020(1):niaa018.
- Noguchi W, Iizuka H, Yamamoto M, Taguchi S. (2022) Superposition mechanism as a neural basis for understanding others, Sci Rep, 12(1): 2859.
- Ryuzo Hirota, Hayato Saigo, Shigeru Taguchi (2024) Reality of Affordances: A Category-Theoretic Approach, Proceedings of the 2024 Artificial Life Conference. (p. 71). ASME. https://doi.org/10.1162/isal_a_00805
- / ツイートする
- / 投稿日: 2025年05月19日
- / カテゴリー: [吉田+田口「行為する意識: エナクティヴィズム入門」]
- / Edit(管理者用)
お勧めエントリ
- 細胞外電極はなにを見ているか(1) 20080727 (2) リニューアル版 20081107
- 総説 長期記憶の脳内メカニズム 20100909
- 駒場講義2013 「意識の科学的研究 - 盲視を起点に」20130626
- 駒場講義2012レジメ 意識と注意の脳内メカニズム(1) 注意 20121010 (2) 意識 20121011
- 視覚、注意、言語で3*2の背側、腹側経路説 20140119
- 脳科学辞典の項目書いた 「盲視」 20130407
- 脳科学辞典の項目書いた 「気づき」 20130228
- 脳科学辞典の項目書いた 「サリエンシー」 20121224
- 脳科学辞典の項目書いた 「マイクロサッケード」 20121227
- 盲視でおこる「なにかあるかんじ」 20110126
- DKL色空間についてまとめ 20090113
- 科学基礎論学会 秋の研究例会 ワークショップ「意識の神経科学と神経現象学」レジメ 20131102
- ギャラガー&ザハヴィ『現象学的な心』合評会レジメ 20130628
- Marrのrepresentationとprocessをベイトソン流に解釈する (1) 20100317 (2) 20100317
- 半側空間無視と同名半盲とは区別できるか?(1) 20080220 (2) 半側空間無視の原因部位は? 20080221
- MarrのVisionの最初と最後だけを読む 20071213