[月別過去ログ] 2009年03月
« 2009年02月 | 最新のページに戻る | 2009年04月 »2009年03月29日
■ 今年の生理研研究会のテーマは「意識」。参加応募、ポスター募集始まってます
(3/17に投稿したものを増補して新たなエントリとして作成し直しました。神経科学大会のwebサイトのアップデートがありましたので、それに対応していろいろ情報を追加しております。)
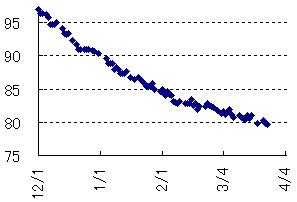
どうもご無沙汰してます。ダイエットの方は順調に18kg減少して、今日118日目で79kg/179cm (BMI=24)となりました。前回の報告( 20090121)のときには「ここからはこの倍のペースぐらいにスローダウンして体重を落としていけるといいのですがね」なんて書いていましたが、それ以降もslopeはぬるくなりつつも低下し続けてます。だいたい狙い通り。本当ですよ? (グラフを載せたがるのは、筋トレをしているやつがすぐに上半身裸になりたがるのと同じ心境。)
さて、今年で3年目の生理研研究会ですが、国際研究集会としての開催が確定しました。つまり、会じたいの規模としてはこれまでの研究会程度のもの(トータルで100人程度)を想定していますが、海外の演者を呼ぶためのお金が付いて、英語での発表、質問を前提とした国際ワークショップとして開催されます。
今年のテーマは「意識」。以前のエントリ(20080913)でも予告しましたように、カルテクの土谷さんとわたしのふたりでオーガナイズしてます。
Webサイト作りました。日時は2009年9月19-20日、名古屋で行われる神経科学大会(2009年9月16-18日)にひきつづいて岡崎に移動して(電車で30分です)の開催となります。
神経科学大会のほうでも関連する企画が3つあります。
まず一つめがChristof Kochによるplenary lecture。
もうひとつが企画シンポジウムでの「意識の脳科学の最前線」です。オーガナイザーが伊佐教授とカルテクのChristof Koch。演者はKochと私吉田、それからハインリヒハイネ大学のPetra StoerigとNYUのNed Block。外国からの招待が3人、Petra StoerigもNed BlockもBlindsightとは関係の深い方です。
ちょっとここらで補足説明。Petra StoerigはAlan Coweyとともにnhpでもblindsightになることを示したNature 1995の著者であるだけでなく、ヒト患者でのblindsight研究で色識別能力の残存を見つけてNature 1986を出してます。Ned Blockは哲学者ですが、consciousnessを[報告などの行動と結びついたaccess-consciousness]と["what-it-is-like"というふうに表現されるような現象的な意識phenomenal-consciousness]とに分けるという議論(Behavioral Brain Sciences 1995)などから神経科学のデータに基づいた議論を行ってきた方です。ちなみにこの1995年のBBS論文で一番最初に出てくる話がblindsight。
それからもうひとつが公募シンポジウムで、カルテクの土谷尚嗣さんとロンドン大の金井良太さんとがオーガナイズしている「錯覚・視覚イリュージョンの脳内メカニズム - 心理物理、脳刺激、電気生理、薬理学的アプローチ」です。こちらも海外で研究中の日本人2人と外国人2人です。
でもって、国際ワークショップのWebサイトの方を見ていただきたいのですが、もう参加応募、ポスター募集が始まってます。海外からの参加者による応募のことを考慮して、今年は早めに受付を始めてます。思い立ったらぜひすぐお申し込みを。
確定している演者のリストももう出てます。以下の通りです。いまのところ、外国人6人、海外で研究中の日本人2人、日本人3人という顔ぶれでして、国際色豊かと言っていいかと思います。旅費どうやって捻出すんの、ってかんじ(<-言っちゃダメ)。
演者の顔ぶれは、昨年台北で行われたASSC12 (Association for scientific study of consciousness)を引き継ぐことを強く意識したものとなっています。オーガナイザーとしては、国際シンポジウムを日本で開催するプレASSCミーティングというかんじを目指したいと考えているわけです。
台北のASSC12に関しては今年はわたしはレポートを作りませんでしたが、予習編がこちら:20080524。UCLの金井良太さんのブログでの感想がこちら:ASSCが終わってから考えたこと。
Ned Blockを呼んでp-consciousnessとa-consciousnessとの関係について話してもらってみんなで議論する、というのを日本でもやろうというわけです。また、台北でのわたしのセッションはLeopold研のAlex Maier、次が私吉田、そのつぎがOlivia Carterのmotion-induced blindnessの話、そして次が金井良太さんのfadingの話、というかんじだったのですが、Alexは昨年神経科学大会でしゃべってもらったので、今年はMelanie Wilke(Leopold研からRA Andersen研へ移りました)にしゃべってもらうとして、そのままそっくりのメンバーに今回の国際シンポジウムにも来てもらったというわけです。しかもそれぞれにいくつかネタを持ってますので、神経科学大会の方でしゃべることと岡崎の国際シンポジウムで話すこととは極力別のことになるような報告で話が進んでます。
会の内容としては、これまでの生理研研究会のポリシーを引き継いで、いくつかテーマを絞った上で議論の時間を取れるようにしたいと考えております。プログラムに関しては近日中に発表予定。もう骨組みは出来てます。プログラムの都合上、以前の予告で書いた日本語チュートリアルはなくなる予定です。
ポスターセッションは一日目の夕方。Poster awardも作る予定です。応募される方は国際シンポジウムWebサイトをごらんいただきたいのですが、まず参加登録をしていただいて、そのあとでwordで要旨提出、という順番になります。
さあ、いよいよ始動しました。ひきつづき演者の方の仕事について予習シリーズなどを始めてこのブログでも盛り上げていく予定です。多くの方の参加をお待ちしています。それではまた! ダイエット後の私が体重を維持できているかどうかを見るという目的でもけっこう!! 今年の秋の連休は意識週間ということでよろしく!!!
Confirmed speakerのリスト:
- Ralph Adolphs (Caltech)
- Ned Block (NYU)
- Olivia Carter (U of Melbourne)
- John-Dylan Haynes (Humboldt-University Berlin)
- Ryota Kanai (UCL)
- Christof Koch (Caltech)
- Shin'ya Nishida (NTT Communication Science Lab)
- Petra Stoerig (Heinrich-Heine-University)
- Naotsugu Tsuchiya (Caltech)
- Melanie Wilke (Caltech, NIMH)
- Takamitsu Yamamoto (Nihon Univ.) (lab web site)
- Masatoshi Yoshida (NIPS)
- / ツイートする
- / 投稿日: 2009年03月29日
- / カテゴリー: [生理研研究会2009「意識の脳内メカニズム」]
- / Edit(管理者用)
2009年03月23日
■ Mutual informationとdecoding
さてさて4日連続投稿、のはずが遅れてしまいましたが前回のつづきです。これまでで最長エントリではないかと思います。
Mutual_informationとdecodingの関係ということがずっとあたまに引っかかってました。ひとつは以前のわたしのエントリ(「「補正」が必要なのは、モデル化が不充分である証拠 」)でmutual informationのupward biasについて書いたときに、最上さんのブログエントリ(「情報量の有用性、補正、ビニング」)でレスポンスをいただいていて、近日中にレスポンスしますと言ったきり放置中だったということがあります。ただそれだけではなくて、BMI関連につなげてencoding-decodingについてもっときっちり考えておきたいと思っていたのですけど、ずっと手つかずのままでいたということもあります。Kay et.alのNature 2008とMiyawaki et.al.のNeuron 2008についてきっちり読んでおきたいのですが、まだそこまでたどり着けてません。vikingさんのところで神谷さんとの非常に興味深いやりとりがあるのですが。
そういうわけで、今回はmutual informationのほうに重きを置いて、いろいろ読んで考えたことをまとめておきたいと思います。最上さんのエントリへの直接的返答というよりはそれに刺激されてエントリを作成したという側面のほうが強いです。直接的なレスポンスに関してはいちばん下で書きます。
んで、以前のわたしのエントリですけど、
超背伸びして書きました。怪しいところをwebで確認したりせずに書いた。もうしらない。厳しくせずに、褒めて伸ばしてほしい。
で、情報理論ってなんか嫌いなんですよね。っていうかニューロンの発火の解析関連での情報理論の応用ってのが嫌いってのが正しいのか。
というかんじで逃げをうちながら極論を言ってたのでかんじが良くなかったなあと思います。そのときはmutual informationそのものの話よりかは「補正」が必要な場合の例のうちのひとつとして挙げたつもりでいました。、昔勉強したとき("Spikes" MIT pressが出版された時代)の記憶をたどりながらなんでかなりあやふやな話でしたが。ただ、せっかくレスポンスがいただけたので、いい機会ですからmutual_informationのupward biasの問題について現状に追いついてみようと思います。というわけでいくつか論文を読んでまとめてみます。まずはこちらから:"Correcting for the Sampling Bias Problem in Spike Train Information Measures" Stefano Panzeri, Riccardo Senatore, Marcelo A. Montemurro, and Rasmus S. Petersen. J Neurophysiol 98: 1064-1072, 2007
まずは導入ですが、刺激sと応答rとのあいだのmutual information MI(s,r)は二つのエントロピーの引き算:MI(s,r) = H(r) - H(r|s)で計算できます(direct method)。それぞれのエントロピーはresponse entropy: H(r) = Σp(r)*log2(p(r))、noise entropy H(r|s) = ΣΣp(s)*p(r|s)*log2(p(r|s))として計算されます。Mutual informationのバイアスとは、けっきょくのところその元となるエントロピーのdownward biasを反映しています。つまり、試行数が少ないとき(rの場合の数K << 試行数Nを満たさないとき)、rの分布が正確に推定できないため、エントロピーが低く計算されてしまう。しかも、この効果はnoise entropyのほうが大きいから(試行数が少ないから)、mutual information全体としてはupward biasとなる、というわけです。
それでこれを補正するために使われるのがMiller-Madow補正(1955)というやつで、これをニューロンのスパイクの例に応用したのがPanzeri and Treves (1996)でした。これが最上さんが説明してくださった、p*log(p)をテーラー展開をして二次の項までを見たときの近似値の話でした。ちなみにPanzeri and Treves (1996)でベイズ推定をしているのはこの補正でのbin数(R, R_s)についてですので、わたしがイメージしていたベイズ的なmutual informationの推定というのとは少々違っているようです。
わたしがイメージしていたような、trial数が充分あることを仮定していないときのmutual informationの推定というものは
- Wolpert DH,Wolf DR (1995) "Estimating functions of probability distributions from a finite set of samples."(pdf) Physical Review E 52: 6841-6854.
- Ilya Nemenman, William Bialek, and Rob de Ruyter van Steveninck (2004) "Entropy and information in neural spike trains: Progress on the sampling problem"(pdf) Physical Review E 69, 056111
あたりのことだったようです。ここで前回の比率のベイズ推定のエントリの応用問題ですが、応答rはK binあるので多項分布です。多項分布の自然共役分布はDirichlet分布となりますので、これをpriorとおいてベイズ推定をします。あるk binでのスパイク生成率の最尤推定値がy_k/n (実データでnスパイクのうちy_kスパイクがk binに落ちた場合)だったとすると、priorをa_k/A (k binのcountをa_kとして、A = Σa_k)とおくと、あるk binでのスパイク生成率のMAP推定値は(y_k + a_k)/(n + A)となります。でもってnoninformative priorだとa_k = A/K (K=bin数)となるというわけです。(このへんはHausser and Strimmer "Entropy inference and the James-Stein estimator, with application to nonlinear gene association networks"(pdf) の説明を使いました。)
後者のNSB entropy estimation methodは、これをさらに改良して複数のDirichlet分布の重み付けみたいにしてやると推定が良くなることを見つけた、という話でした。これは元のPanzeri and Treves (1996)よりもbiasが少ないということで優れています(Figure 3A,B)。たしかに、良くも悪くもpriorの選択の善し悪しが推測の成績に大きく影響を与えるようです。
このような状況でPanzeri and Trevesが巻き返しを図ったのが、
Montemurro, Senatore and Panzeri "Tight Data-Robust Bounds to Mutual Information Combining Shuffling andModel Selection Techniques" Neural Computation 19, 2913-2957 (2007)
であるようです。この論文はnoise correlationのうちでcorrelationのない成分H_ind(r|s)を計算したり、刺激と応答をシャッフルしたH_sh(r|s)を使ってやると、NSB methodよりも優れた成績のときがある(Figure 3C, D)というものなのですが、なんか部分的な改善というかんじでわたしにはあまりピンと来ませんでした。
ともあれ、これがだいたいPanzeri et.al., JNP 2007の内容でした。
さてさてまだつづきます。直接バイアス問題に関わるわけでもないのですが、entropyおよびmutual informationの信頼区間のベイズ推定をしたという仕事があります:
- Kennel, M., Shlens, J., Abarbanel, H. D. I., Chichilnisky, E. J. (2005). "Estimating entropy rates with Bayesian confidence intervals." Neural Computation, 7, 1531-1576.
- Jonathon Shlens, Matthew B. Kennel, Henry D. I. Abarbanel, E. J. Chichilnisky. (2007). "Estimating Information Rates with Confidence Intervals in Neural Spike Trains." Neural Computation 19:7, 1683-1719.
前回のエントリで比率の推定についてMLEおよびベイズ推定によって推定のばらつき具合を評価して信頼区間を求めましたが、エントロピーも有限個のデータがどのbinに落ちるかという確率から推定されるものですので、同様なアプローチが可能です。エントロピーおよびmutual informationについて、多項分布のMLEから信頼区間を計算したもの、さらにMiller-Madow補正をしたもの(信頼区間には変化無し)、ベイズ推定で信頼区間を計算したものを提示しています。
Mutual informationも比率のデータと同様、信頼区間が付いたものとして扱うのが筋だと思いますので、こういう形で統計に乗っけてやるのがいいんじゃないかと思いました。そもそもmutual informationで出てくる数字のバイアスを問題にしていたのは、いったんinformation rateが計算された後にそれが確定した値として統計で扱われるというあたりに違和感を持っていたからだったわけです。(ROCがひとつの確定した値として一人歩きするのと同じ。) 思えば統計的な扱いとmutual informationとを対立させるというよりは、mutual informationという量を統計的に扱ってやるというのが正しいアプローチなのかもしれません。
まだつづきます。わたしがこのへんの論文を読んでいた動機の一つは、さいきんはやりのencoding-decodingのスキームと、mutual informationを用いた解析とはどういう関係にあるかという点でした。ちょっと話は飛びますが、encoding-decodingの話のほうでさいきん読んだレビューについて言及します:
Wu MC, David SV, Gallant JL. "Complete functional characterization of sensory neurons by system identification."(pdf) Annu Rev Neurosci. 2006;29:477-505.
これはvisual neuroscienceの分野で使われているreverse correlationとかspike triggered averageとかm-sequenceを使ったsystem identificationとかSVMを使った推定といった、刺激sからニューロンの応答rへの変換r=f(s)のfを推定するすべての研究についてMAP推定の一種として捉えてまとめたレビューです。MLEもpriorを使わないMAP推定の一種として捉えられるし、parametricなWiener-Volterra展開的なアプローチも、SVMを含んだカーネル法によるnonparametricなアプローチもモデル選択の違いとして統一的に捉えられることを示しています。このようにしてモデルを作成して、MAP推定(点推定)をしてやって、corss validationをしてやってモデルの善し悪しを評価する、というスキームが示されます。
このコンテクストの中では、mutual informationはモデル選択の善し悪しの評価法としてcorrelation coefficientなどと並列して扱われています(correlation coefficientと比べてmutual informationの方がよいかどうかはわからない、みたいな記載があります)。たしかにそうして考えてみると、mutual informationというのは統計解析の中でいうR^2に対応したものと考えることが出来るのではないでしょうか。データが有限ならupward biasを持っているという意味でも似ています。そういう意味では、mutual informationのオリジナルな意味、データの伝達の正確さの評価に戻って、mutual informationの定量化がなにをしているかということを考える意義があります。
さてこのようなencoding-decodingのスキームと、mutual informationを用いた解析とはどういう関係にあるか。その意味でJonathan D. Victorのこれらの論文に書いてあることは非常に役に立ちました。
Jonathan D. Victor. 2006. "Approaches to Information-Theoretic Analysis of Neural ActivityApproaches to Information-Theoretic Analysis of Neural Activity." Biological Theory 1:3, 302-316.
Jonathan D. Victor, Sheila Nirenberg "Indices for Testing Neural Codes" Neural Computation, December 2008, Vol. 20, No. 12, Pages 2895-2936
前者にはShannon entropyでできることの限界を強調してます。後者では情報理論的解析とベイズ推定とを並列的に扱って、どちらを使うのが刺激sから応答rへのcodingの問題(あるコーディングが使われている可能性を除外する方法)に向いているかの異論をしています。前者の論文にはこう書いてあります:
Fundamentally, the Shannon theory was designed for characterizing communication systems whose principles were understood, not for the "inverse problem" of determining the principles by which a system works from observations of its behavior.
それからこちら:
Moreover, the Shannon theory does not attempt to describe the relationship between a sensory or motor domain and neural activity (i.e., the nature of the neural representation) but merely provides an index of how faithful this representation is.
そういう意味では、direct methodのいいところは、刺激sから応答rへの変換に関して明示的にモデルを作らなくてもmutual informationを計算することによって、encodingの過程についてなんらか示唆を得ることができるという点にあるのでしょう。ただし、まったくassumption-freeなわけではなくて、応答rのbinの切り方とか、時間幅の問題とか、そういうところで隠れてcodingのモデルが入り込んでいるんじゃないかと思うのです。長々と書きましたが私の主張はなにかといいますと、刺激sと応答rとはものすごく違った構造をしているわけでして、その二つをつなげるmutual information MI(s,r)を作るために、非明示的にモデルのassumptionが入っているので、direct methodというものはなんか変なんじゃないのか、ということです。
Reconstruction methodのほうはmutual informationの計算という意味ではずっとクリーンです。MI(s,r)の代わりに応答rからdecodeした刺激s_estを使ったMI(s, s_est)を計算するわけです。刺激は自分でデザインできるからbinとかの問題もクリヤーだし、なによりsと s_estという、同じ構造のものを比較しているわけですから。もちろん、MI(s, s_est)はモデル化が悪ければいくらでも下がるので、lower boundしか決めることができない( MI(s, s_est)<=MI(s,r) )わけですが、reconstruction methodははモデル化の部分を上記のMAP推定的なスキームに任せて、mutual informationをモデルの評価に限局して使うということで、こっちだけにしといた方が良いんではないだろうか、という気がしてきたのです。
まあ極論ですが。実際には、刺激空間がよくわかっている低次視覚野ならばモデル化のほうからアプローチする方が効率がよいし、高次視覚野ではなるたけ最適刺激にassumptionをおかずに多くの種類の刺激を使って応答を見て、それを比較的応答モデルに対するassumptionの少ないmutual informationで評価してcodingについての示唆を得る、というのが現実的であるということなのでしょう。
さてここまで書いたところでPanzeriがQuirogaといっしょに書いたレビューが出ました。これについても読んでおきましょう:
Rodrigo Quian Quiroga and Stefano Panzeri "Extracting information from neuronal populations: information theory and decoding approaches"(pdf) Nature Reviews Neuroscience 10, 173-185 (March 2009)
現在の文脈で重要なのは、"Complementarities of decoding and information theory"のセクションなのですが、decodingはposteriorのarg maxをとっている(MAP推定をしていちばんもっともらしい刺激を推定する)のに対して、mutual informationはそれ以外にも情報があることを定量化している、という点を強調します。だから、mutual informationでは2番目にlikelyな刺激についての情報とか、ある図形が非常にunlikelyであることとかも持っているだろう、というわけです。
ただこれって、あくまでMAP推定に限局した問題だと思うんですけどね。posteirorの情報を持っているということは、確率密度分布を持っているわけだから、刺激26がmost likelyだけど、刺激29もそのつぎにlikelyだとかそういうことはdecodingの方でも言えるわけですよね。だからあまり説得的に思えないのですが。
どうやってdecodingとmutual informationを組み合わせるかという点では、decodingできたinformation MI(s, s_est)をdirect methodによるMI(s,r)との比率で評価する(「95%の情報がdecodeできている」といった評価ができる)ということが書いてあって、これはいいなと思いました。つまり、BOX3に書いてあることですが、われわれがdirect methodで計算しているmutual informationというのは応答rそのものではなくて、rをカテゴリー分けしたりいくつかの処理をしたf(r)なわけです。(さっきわたしはこの点を捉えて、非明示的なモデリングが入っている、と指摘したわけですが。) すると、
MI(s,f(r)) < MI(s,r)
が成り立ちます。そのうえで、reconstruction methodで使われるdecodingでも、けっきょくまったく同じ形でのrの変換(r -> f(r))が不可避なわけです(spike countのカテゴリー化であれ、時間windowの幅であれ)。だからdecodingによる逆変換をg()としておくと、reconstruction methodによって計算できるmutual information MI(s, s_est)では、
MI(s, s_est) = MI(s, g(f(r)) <= MI(s,f(r)) < MI(s,r) MI(reconstruction method) <= MI(direct method)
がなりたちます。Upward biasの問題は依然つきまといますが、そういう意味では、decodingのperformanceの評価としてはいいんではないかと思います。この、direct methodとreconstruction methodで挟むという話自体は新しいものではなくて、私自身は以下のような論文で見ましたが、もっと広く使われてもいいと思いました。
- Borst A, Theunissen FE. "Information theory and neural coding." Nat Neurosci. 1999 Nov;2(11):947-57
- Buracas GT, Zador AM, DeWeese MR, Albright TD. "Efficient discrimination of temporal patterns by motion-sensitive neurons in primate visual cortex." Neuron. 1998 May;20(5):959-69.
あとはdecodingの成績をまとめたconfusion matrixを元にしてmutual informationでの「次元の呪い」を除けないか、みたいな話も。これもdecodingとmutual informationとを組み合わせる方法として有望だと思いました。
イントロの部分でdecodingとmutual informationがどんな風に"intrinsically related"であるかを示すことを目指す、ってあったんですが、ここについてはあまり満足がいくかんじがしません。
思うんですけど、どんな風に"intrinsically related"であるかって、ベイズ推定はp(s|r) ∝ p(r|s) * p(s)を使っていて、mutual informationはp(r)とp(r|s)を使っていて、共通のものを使って計算しているという意味でintrinsically relatedなわけですよね。それなら、ベイズ推定の計算から推定されたp(r)とp(r|s)でもってmutual informationを計算する、みたいなことをすれば良いんではないのでしょうか。p(r)とかは積分しないといけないわけですけど。ベイズ推定の方はcross validationが使えるけど、mutual informationのほうはそれに対応したものがない(shuffleしたもの?)というあたりが推定の問題でもあるわけだから、同じ確率密度分布を共有して計算することで推定の確かさも揃えて扱うことができるんじゃないでしょうか。ちょっともう素人がわかったような口をきいてるかんじのもの言いになってる気がするんで恐縮ではあるのですが。
さて、いろいろ書きましたが、もちろん統計解析と情報理論は深いところで繋がりあっているので、そのへんをもう少し勉強しなくちゃなあと思ってます。その意味では情報幾何での、mutual information - fisher information - KL divergence - maximum likelihood estimationあたりを包括して捉えられる図式を勉強しなきゃなあ、ということで「新版 情報理論の基礎」村田昇を読むのを自分の宿題にしてます。
ふと思い立って村田昇教授のサイトを見たら「少数データを用いた推定」というのを発見。KL情報量よりrobustなBregman情報量というものがあるらしい。きりがないのでこのへんまでとします。
さて、以上を踏まえて、最上さんのブログエントリ(「情報量の有用性、補正、ビニング」)に応答してみたいのですが、補正公式、ベイズ統計関連、binningなどについては以上ですでに言及しました。脳が尤度推定やベイズ推定をしてるという最近の話題には私も興味があるし、とくに意見の相違はないですね。この話題と解析としてのベイズ推定とを混同しないほうがよい、というのはたしかにそうだと思いました。ただ、これも深いところで通底しているような気がしてますが。
ベイズ統計の是非の話というのはじつは二層あって、[頻度主義 vs. ベイズ主義(モデルパラメータthetaを固定しているとするか、確率変数としてとらえるか)]という話と[priorを使わない(MLEまで) vs. 使う(MAP推定、ベイズ推定まで)]という話があるのではないかと思います。今回の話は後者でした。脳が確率密度分布を持っているってのはどちらかというと前者の話だったのではないかと思います。
後者の問題に関してですが、前回のエントリを作りながら思ったのですが、あるていど単純な問題にはベイズ統計はいらないし、それなりに複雑な問題で、priorを使わないと明らかに損しているようなモデルではpriorを使うことによって道が開けるわけです。それぞれの実験の状況で、利用可能なデータ量(maximum likelihood)と、利用可能なpriorとによって、どっちがより効率のよいモデルを作れるかによって決まるんではないかと思います。充分データが集めることができて、それで充分なforward modelを作ることができるならMLEのほうがよいし(priorを使うことによる不安定性を回避できる)、データ収得に限りがあるようなら、priorを使ったほうが推定の成績と効率は良くなる。でもって、脳計測の場合はしばしばデータ収得に限りがある状況のほうが多いのではないでしょうか。(「物理をやっていた者の思考として自然」というのは統計物理のように前者が妥当な状況でのことではないでしょうか。)
あと、ぶっちゃけ情報量の利用はプラグマティックな意味でも役に立ちます。
これ以降の部分での複数ニューロンのデータの集積に関する話は、データいじっている方の実感なので面白いと思いました。じっさい、わたしも解析してていつも悩ましい問題です。ただ、別のニューロンのmutual informationを足すというのはその意味上よいのでしょうか? つまりmutual informationの単純な足し算というのは、別々のニューロンが独立した情報を持っているときの情報量を意味しているわけで、そうすると、意味がありすぎると思うのです。一般的なsingle-unit recordingのデータで同時記録をしていないデータを集める場合、多ニューロンのmutual information量の集積は、それらの複数のニューロンのデータから抽出可能な(提示した図形に関する)情報量を計算することとして捉えることができます。そうすると、複数のニューロンのデータを足していけば、似た反応特性を持っている分、得られる情報量の増加は目減りしていくわけで、単純な足し算をするよりかはこういった反応選択性の相関を考慮した集積をしたほうがよいのではないでしょうか。ちょっと発想がdecodingに寄りすぎているのかもしれませんが。
あと、上記のPanzeri et.al., JNP 2007を読んだかぎり、direct methodによって、biasの問題に対処して意味のあるmutual informationを計算するためには、NSB methodのような現状でいちばん良いものですら N_s > 2-4 R (R: 全応答の場合の数)という縛りがあるわけです。そうすると、たとえば5ms windowで0/1 spikeに分類してtime window 8個分でR=2^8=256としても、N_s (刺激ごとの試行数)に500trial以上必要なわけですから、RSVP使うとかしてN_sを相当稼がないといけないわけです。いったんこういう数字を見てしまうと、direct methodを使ったmutual informationの計算というのはかなり敷居が高いんではないだろうか、と思いました。
以上です。長大になりすぎましたが、こうやって書いていくことでまえに考えていたときよりはずいぶんいろいろ明確になってきました。レスポンスしてくださった最上さんにお礼申し上げます。
# viking
僕のblog(しかもモメたエントリ)にリンクをいただいて大変有難いのですが、今回の件とfMRI mind-reading studyの件ってそんなに関連していますか? 工学系出身の身としては、fMRIでmind-readingというのはもっと泥臭い部分(良くも悪くも力業)の話だと思っておりますもので・・・あくまでも比較の問題ですが、むしろERP/MEGの逆問題推定の方が話題としては親和性が高いかもしれませんよ。
# pooneilどうもおひさしぶりです。前者が「力業」に帰結する話なのかどうかはまだ私は勉強不足なのでよくわかりません。そこへ辿りつくための枠組みあたりをまとめているつもりです。ほんとうは立場上、そんなのんきなこと言っているようではいかんのですが。後者が親和性が高いことは二百も承知でして、それが以前にLFPのまとめを作ったりしたことと関係してたりします。
# vikingmind-reading methodのチュートリアル的な総説がNeuroImageに出てます。ご参考までに。
Machine learning classifiers and fMRI: a tutorial overview (Pereira F, Mitchell T, Botvinick M, Neuroimage. 2009 Mar;45(1 Suppl):S199-209)
http://dx.doi.org/10.1016/j.neuroimage.2008.11.007
2009年03月19日
■ 比率のデータにエラーバーを付けたいんだけど
最高ですか! (<-奇をてらったごあいさつ)
どうもご無沙汰しております。ここに書いているということは暇だということを必ずしも意味しないけれど、ここに書いてないということはかならず忙しい。んで、しばらく頭の中をぐるぐる回っていたものがあったので、そのへんを吐きだしてすっきりさせて論文書きに集中したいと思いますので、いろんなところに不義理を働きつつもこんなもの書かせていただきます(超低姿勢)。
...なんて前口上をつけた原稿を作ってあったんだけど、なぜか久しぶりの三日連続投稿に。
んで、いきなり口調が変わるのですが、比率のデータにエラーバーを付けたくならないっすか?なんでもいいんだけど、たとえば二択の課題の成績が試行数120で正答数73で正答率61%だったとします。これは二項検定によって両側検定5%水準でchance level (50%)よりは有意に大きいです(図1の(1))。それを直感的に示すようなエラーバーをバーチャートに付けたい。これが今回の問題です。
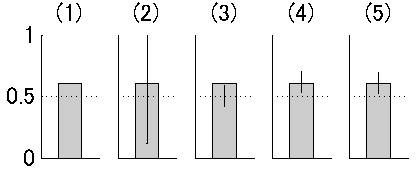
図1
普通は比率のデータにエラーバーなんて付けません。73/120という一つのデータだと思われているからでしょうね。でももしこれが正答数でなくて、反応潜時のデータかなんかだったらもちろんSDを付けることができます。同じように、73/120というデータのばらつき具合にエラーバーを付けてやりたいと思うのですよ。
まずは、間違った方法ではありますが、正答に1、誤答に0を割り振って、たんにそのSDを計算します。するとmean = 0.61, std = 0.49という値が出てきます(図1の(2))。もちろんこれは誤差の分布を正規分布と仮定しているのが間違いなわけです。(これをgeneralized linear modelでリンク関数をbinomialにして計算すれば間違いにはなりません。これは最尤推定でやっていることと同じのはずです。これについては後述。)
それでは今度は、比率の検定に基づいて考えてみましょう。ここでは二項検定で検定をしているわけですからそれを反映させましょう。つまり、試行数120で帰無仮説H_0:母比率p=0.50の場合の二項分布Bi(n,p) = Bi(120, 0.50)を計算します。Rだとこんなかんじ:
total <- 120 correct <- 73 x <- seq(0, total) bino_prob1 <- dbinom(x, total, 0.50) plot(x,bino_prob1)
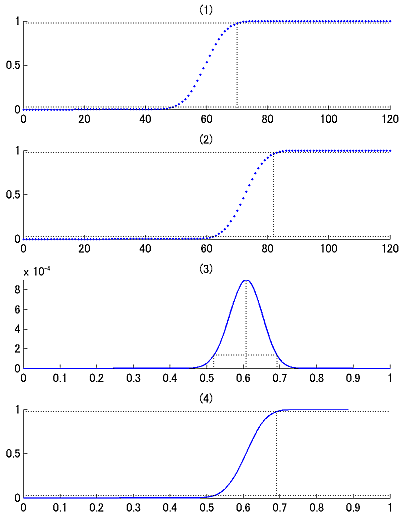
図2
両側検定5%有意水準で正答数70以上もしくは48以下だと有意です(図2の(1))。今回は73だから有意でした。この範囲を図に無理矢理入れるならこんな図(図1の(3))になりますが、こんなの誰も望んでない。だいたい試行数にしか依存してないし。
同じ発想で母比率が73/120だったときに実データがどのくらい散らばるかということを二項分布Bi(120, 73/120)
total <- 120 correct <- 73 x <- seq(0, total) bino_prob2 <- dbinom(x, total, correct/total) plot(x,bino_prob2)
で評価してやることも出来ます(図2の(2))。こうするとエラーバーの範囲は[0.5167 0.6833]となります(図1の(4))。これはもっともらしいですが、統計的な裏付けに欠けます。
さてこのへんからが本題です。Maximum likelihood estimationを考えてみましょう。データ73/120は既知で確率theta = 0-1のほうが変数で、尤度関数は
likelihood ∝ theta^correct * (1-theta)^(total-correct)
となります。
theta <- seq(0,1,1/total) likelihood <- theta^correct * (1-theta)^(total-correct) Lc <- likelihood / sum(likelihood) plot(theta,Lc)
このピーク値を見るとたしかに0.61になっていて、correct/totalがthetaの最尤推定値になっていることが確認できます(図2の(3))。またさらにこの尤度関数のcumulative density functionを作ってやると(図2の(4))、最尤推定値の95%信頼区間を[0.519 0.691]というふうに評価することが出来ます(図1の(5))。
この値は図1の(4)とほとんど変わりません。両者の違いは、二項分布では横軸xがデータの個数で離散的になっているのに対して、最尤推定では横軸thetaが連続値になっているという点ですが、thetaのほうを離散的にして計算すると(theta = [0:1/120:1]としてやる)微妙に違う値になります(図3の上 緑が二項分布、青が尤度関数、図3の下 緑が尤度関数-二項分布の引き算)。数学的にはべつものなんでしょう。つまり、二項分布Bi(n,r,p)のグラフを縦に見るか横に見るか、という話になります。くわしくは「ベイズ統計学は本当に有効か?」赤嶺達郎および「枠どり法とPetersen 法の区間推定における伝統的統計学とベイズ統計学との比較」 赤嶺達郎(pdf)(今回の話のネタ元のひとつ)を参照、ということで。
Webを探したら「検定と区間推定」奥村晴彦(TeX本で有名な方)にRでのimplemantationがありました。なんかこれを読むといま書いたことのすべてが書かれているような気がしますが、まあこうやって書いてみることは悪くないことで。
> binom.test(73,120,0.5)
Exact binomial test
data: 73 and 120
number of successes = 73, number of trials = 120, p-value = 0.02208
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.5150437 0.6961433
sample estimates:
probability of success
0.6083333
ともあれ最尤推定まで考えると、それなりに意味のあるエラーバーが書けそうです。役に立つと思うんですけど、なんでみんな使わないんですかね。
さて、こんなことを計算している目的の一つはベイズ統計のお稽古だったわけで、「ベイズ統計学入門」渡部洋著を元にしてさらに先に進みます。
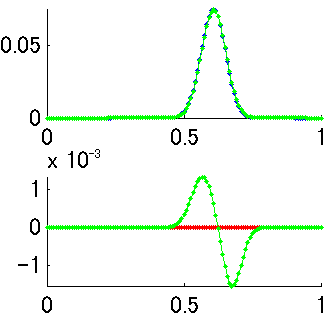
図3
Maximum likelihood estimationで得た最尤推定値はベイズ統計の立場から見れば、無情報のprior (p(theta)が一定)を用いたときのMAP推定値と等価です。つまり、さっきの尤度関数(図2の(3))はposteriorの分布と捉えることが出来て、点推定をするとピーク値の0.61を取ることになり、区間推定をするなら図2の(4)のように信頼区間を計算することが出来ます。
ベイズ統計の場合には、信頼区間(confidence interval)ではなくて、信用区間(credible interval)として、全体の10%の面積が除外されるような縦軸の値を設定して計算します(図2の(3))。これはMAP推定自体がピーク値(mode)を使っていて、median (=50% percentile)ではないということからすれば納得がいきます。こうして計算された信用区間は[0.520 0.692]となります。これはさっきの信頼区間の値[0.519 0.691]とほとんど変わりません。分布が歪んでないのでそりゃそうでしょうね。
教科書まる写し口調ですが、今まで扱ってきた二項分布をBi(total, correct/total)と表現しておくと、この尤度関数L(=ベイズ統計でのposterior)はベータ分布Be(correct+1, total-correct+1)と表現できます。二項分布のベイズ推測での自然共役事前分布がベータ分布であることがわかっています。つまり、priorがベータ分布なら、posterior ∝ likelihood * priorもベータ分布ということ。
無情報のpriorを使う場合にはこれはBe(1,1)と書けて、これはpriorではtotal=0, correct=0となっていることと等価です。このときのposteriorは
posterior ∝ likelihood * prior = Be(correct+1, total-correct+1) * Be(1,1) = Be(correct+1, total-correct+1)
となるわけです。確認のためこのベータ分布をplotしてみますと、これまでの尤度関数とまったく一致します(図3の上 赤がベータ分布だが青に重なって見えない 図3の下 赤が尤度関数-ベータ分布の引き算)。
面白いのは、ベイズ推定の式がたんにベータ分布の中身Be(a, b)の足し算になっている点ですね。もしここでpriorとして無情報のprior(Be(1,1): total=0, correct=0)を使わずに、局所一様分布のpriorというやつを使うとBe(1/2, 1/2)となります。これはtotal=-1, correct=-1/2としているのと同じということで、これは得られたデータから1 trial分差っ引いてposteriorを作っているということになります。おお! ここでも出てきた補正の思想!
というわけでpriorとしてはBe(1,1)とかBe(1/2,1/2)とかがありうるのだけれど、はっきり言ってこのような単純な状況ではベイズ統計が出てくる必要性はあまりないと言えましょう。ではどういうときに必要かというと、複数のセッションを足し合わせるような状況ですね。(このへんから北大の久保拓弥先生のweb資料(pdf)に依拠しながら進みます。)
これまで使ってきた73/120というデータですが、じつはこれが5回分のセッションの集計だったとします。たとえば、{16/30, 24/30, 12/20, 11/20, 10/20}というデータだったとします。この5点をプロットしてそれのSDでエラーバーを付ける、というやりかたがありますが、これは試行数の120を使ってないので正当な評価とは言えないでしょう。(セッションごとのばらつきを評価しているというのはわかるのだけれど、それが0.5からdeviateしているかどうかを検定するとしたらそれは意味がない。)
データのモデル化を考えてみると、各セッションごとに二項分布Bi(n, 73/120)から出てきたと考えるとします。これはセッションごとにthetaが一定(=73/120)であるとするモデルですが、二択の心理実験とかではだいたい当てはまらないわけです(これはoverdispersionが起こっているかどうかで検証できる)。そこでセッションごとのthetaが73/120からばらつく(とりあえず正規分布でSD=0.1として生成してやると{0.52 0.80 0.60 0.55 0.51, ....}となる)というふうにするのがrandom effectモデルで、このSDを決めてやるために経験ベイズ、階層ベイズが出てきて、そうするとセッションごとのばらつきとセッション全部のばらつきとを評価することが出来て、エラーバーとしてもそれを示すのが正しいのだと思うのだけれど、おっとここで時間のようです(<-逃げた)。
いったん逃げたけど帰ってきた。やりかけなんだけどRでの解析を書いておくと、まずデータ作り:
id <- factor(c(rep(1,30), rep(2,30), rep(3,20), rep(4,20), rep(5,20))) y <- c(rep(1,16), rep(0,14), rep(1,24), rep(0,6), rep(1,12), rep(0,8), rep(1,11), rep(0,9), rep(1,10), rep(0,10)) data3 <- data.frame(y=y, id=id)
これをidを無視してセッションをまとめたときの解析は、generalized linear modelでリンク関数をbinomialにしたもので、こんなかんじ:
result1 <- glm(y ~ 1, family = binomial, data = data3) summary(result1)
結果は
> summary(result1)
Call:
glm(formula = y ~ 1, family = binomial, data = data3)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.369 -1.369 0.997 0.997 0.997
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.4403 0.1870 2.354 0.0186 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 160.68 on 119 degrees of freedom
Residual deviance: 160.68 on 119 degrees of freedom
AIC: 162.68
Number of Fisher Scoring iterations: 4
となっていて、Interceptのestimateは0.4403で、standard errorは0.1870。だから比率の最尤推定値および95%信頼区間は
> 1 / (1 + exp(-0.4403)) [1] 0.6083305 > 1 / (1 + exp(-0.4403+0.1870*1.96)) [1] 0.5184366 > 1 / (1 + exp(-0.4403-0.1870*1.96)) [1] 0.6914315
というふうに正しく計算できます。
また、セッションごとにIDが付いたデータの場合はGLMM(混合モデル)を使って、さっきのdata3を解析すると、
library(glmmML) result3 <- glmmML(y ~ 1, family = binomial, cluster = id, data = data3) summary(result3)
というので計算が出来ます。この結果は
> summary(result3)
Call: glmmML(formula = y ~ 1, family = binomial, data = data3, cluster = id)
coef se(coef) z Pr(>|z|)
(Intercept) 0.4337 0.2269 1.912 0.0559
Scale parameter in mixing distribution: 0.2777 gaussian
Std. Error: 0.2753
Residual deviance: 160.2 on 118 degrees of freedom AIC: 164.2
となって、idのrandom effectのSEが0.2753と出てきます。このため、interceptの推定もglmから多少ずれるので、比率の推定も以下のように多少低めに出ていて、信頼区間も広くなっています。ひとつ突出している24/30が効いている分を考慮しているかんじがうかがえます。
> 1 / (1 + exp(-0.4337)) [1] 0.6067568 > 1 / (1 + exp(-0.4337+0.2269*1.96)) [1] 0.497244 > 1 / (1 + exp(-0.4337-0.2269*1.96)) [1] 0.7064955
ただ、glmmMLの結果の見方がまだよくわかってないので("Scale parameter in mixing distribution: 0.2777 gaussian" ってなんでしょう。以前の資料を見るとここはSDが表示されていたんですけど。)、このへんで止まってます。
Chance levelから有意かどうか、というのはgeneralized linear modelまで来ると、H_0のrejectという形ではなくてモデル選択ということになるので、inteceptが0 (比率が0.50)のモデルと最尤推定で得られたinterceptでのモデルとでAICを比較するということになるんでしょう。論文書きのときはpが付けられないと困っちゃうんだけど。
さてさて、ここからが本番です(本気)。長々と引っ張ってきましたが、このエントリの最終目的はじつはmutual informationのバイアス問題に関連しているのでした。有限の試行のデータから刺激sと応答rとの間からmutual informationを計算するときに必要なのはp*log2(p)の計算なわけですが(応答rがK binあるうちのi binに落ちたときの確率をpとする)、このpの最尤推定値として、あるbinに落ちたspike数yとその総数nを実測データから計算してつくったy/nを用いているわけです。このことはエントロピー推定のバイアスを生むわけですが、そもそもcountデータからの比率の推定に基づいているのだから、今回扱ったような手法でエントロピーおよびmutual informationでもベイズ推定と信頼区間を計算してやることが可能となります。
基本に戻ると、刺激sと応答rとのあいだのmutual information MI(s,r)は二つのエントロピーの引き算:MI(s,r) = H(r) - H(r|s)で計算できます(direct method)。それぞれのエントロピーはresponse entropy: H(r) = Σp(r)*log2(p(r))、noise entropy H(r|s) = ΣΣp(s)*p(r|s)*log2(p(r|s))として計算されます。
ここで比率のベイズ推定のエントリの応用問題ですが、応答rはK binあるので多項分布です。多項分布の自然共役分布はDirichlet分布となりますので、これをpriorとおいてベイズ推定をします。あるk binでのスパイク生成率の最尤推定値がy_k/n (実データでnスパイクのうちy_kスパイクがk binに落ちた場合)だったとすると、priorをa_k/A (k binのcountをa_kとして、A = Σa_k)とおくと、あるk binでのスパイク生成率のMAP推定値は(y_k + a_k)/(n + A)となります。でもってnoninformative priorだとa_k = A/K (K=bin数)となるというわけです。(このへんはHausser and Strimmer "Entropy inference and the James-Stein estimator, with application to nonlinear gene association networks"(pdf) の説明を使いました。)
というわけでこれも手計算してみようかと思いましたが、bin数Kが大きいとあっという間に次元が増えてたいへんなので止めとしておきます。ともあれ、mutual informationでもベイズ推定して信頼区間を付けられるというわけです。今日はこんなところまで。あしたにつづきます。
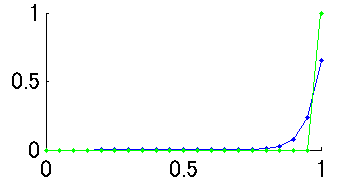
図4
追記:コイダーマンさんからコメントいただきました。どうもありがとうございます。なるほど、図3での緑(二項分布)と青(尤度関数)の違いはcorrect=20; total=20の場合を考えるとより明確になりますね。さっそく図を作ってみました(図4)。二項分布だとcorrect ratio 100%しかありえなくなってしまうけど、尤度関数だとcorrect ratio 90-95%あたりの可能性もそれなりにあるということがこの図だとよくわかります。
# コイダーマン
こんちは。
私も行動実験や心理実験をやってて同じことを悩んでましたヨ!
自分が読めるようなわかりやすい本には図1(4)の説明しか載ってなくて、
でもその方法だと、たとえば正解率が100%(20回中20回とか)のときに
信頼区間がゼロになっちゃうんですよね。
でも、そんなわけない!
真の確率は98%なんだけど、たまたま結果が100%になったってことだって起きるはずだ!
当時は尤度の読み方どころか文字すらも知らなかったので
自分で一から考えて答えにたどり着いたときは感動したです・・車輪の再発明と言うんでしょうか。
適当に二項分布の母確率pを仮定して、
そのときに実験データ(たとえば20回中20回)が生じる確率を求める。
図の横軸を仮定した母確率のpにとって、縦軸を実験データの発生確率でグラフを書くと・・
母確率pは0~1まで均等にあると仮定して、そのpが選ばれるのをΔpと考えると
・・あ、信頼区間が計算できちゃった。やった!って。
Mutual Infomationの信頼区間計算ってのはいいですね!
これまで私はあまり考えずにブートストラップのような方法で求めましたです。
平均発火頻度をポワソン分布でフィッティングして、
試行回数分のデータを擬似発生させて、自分がきめたBINで相互情報量を計算。
これを1000回とか繰り返したら相互情報量のばらつきがわかるかも、とか。
でもこれじゃ
ある刺激への応答が全部0spk/sだったときに信頼区間がゼロになって困る。
繰り替えしが5回とか少なかったりすると、真の平均発火頻度が0以上である可能性は相当高いのに。
続編期待してます。
# コイダーマンあ・・書き込みした後に思い出した・・
二項分布の信頼区間を求めようとしたのは、実験の解析が目的じゃなかった!。ゲームRagnarokOnlineで錬成だったか何かの成功確率が、いくつかの条件間で差があるのかないのかを匿名某で議論してたときのことだったワ!
心理実験やってたから、なんてウソウソでした!
コイダーマン、どうもありがとうございます。(言いにくいのでさん付け省略で。)
なるほど、20/20の例を使えば、図3上の二つのプロットの違いがより明確に示せますね。追記しておきます。
>RagnarokOnlineで
それ正直に申告しなくてもいいよ!!!
つーかそれアカデミックな議論ですね。
わたしも某巨大掲示板で複数のランキングの相関係数を計算して議論したことがあるけど。
2009年03月18日
■ 「意味なんてどこにも無いさ」
The Whoの"so sad about us"を聴いてたらなんかほとばしってきたんでまた書いちゃう。
反復運動は回転運動。
どんな言葉も作り手がコンテキストを設定しなければ、読む側のコンテクストが設定されて陳腐になる。
クヌギの木の下まで行こうぜ / そこにはなんにもないとわかっているけどさ
クヌギの木の下まで行こうぜ / そこにはなんにもないとわかっているけどさ
どうでもいい言葉をマントラのように繰り返して、それで感情を揺さぶる。それがメロディーとリフの力。
だから、反復運動は回転運動なんだ。
お勧めエントリ
- 細胞外電極はなにを見ているか(1) 20080727 (2) リニューアル版 20081107
- 総説 長期記憶の脳内メカニズム 20100909
- 駒場講義2013 「意識の科学的研究 - 盲視を起点に」20130626
- 駒場講義2012レジメ 意識と注意の脳内メカニズム(1) 注意 20121010 (2) 意識 20121011
- 視覚、注意、言語で3*2の背側、腹側経路説 20140119
- 脳科学辞典の項目書いた 「盲視」 20130407
- 脳科学辞典の項目書いた 「気づき」 20130228
- 脳科学辞典の項目書いた 「サリエンシー」 20121224
- 脳科学辞典の項目書いた 「マイクロサッケード」 20121227
- 盲視でおこる「なにかあるかんじ」 20110126
- DKL色空間についてまとめ 20090113
- 科学基礎論学会 秋の研究例会 ワークショップ「意識の神経科学と神経現象学」レジメ 20131102
- ギャラガー&ザハヴィ『現象学的な心』合評会レジメ 20130628
- Marrのrepresentationとprocessをベイトソン流に解釈する (1) 20100317 (2) 20100317
- 半側空間無視と同名半盲とは区別できるか?(1) 20080220 (2) 半側空間無視の原因部位は? 20080221
- MarrのVisionの最初と最後だけを読む 20071213