[月別過去ログ] 2025年06月
« 2025年05月 | 最新のページに戻る | 2025年07月 »2025年06月07日
■ ホメオスタット(homeostat)の挙動を再現してみる
前置き
このブログ記事は著書「行為する意識: エナクティヴィズム入門」のサポート資料として作成された。しかし、この本を読まなくても意味が通るようにこの記事は書かれている。
Matlabのコードは吉田のgithub (pooneil68/homeostat)に置いてある。式やコードの作成ではGemini 2.0の助けを借りたが、自分の目で確認を取った。
本文
精神科医でありサイバネティクスの先駆者であったウィリアム・ロス・アシュビーは、ホメオスタシスを電気回路で実現した「ホメオスタット」という機械を作り上げた(1940年代)。
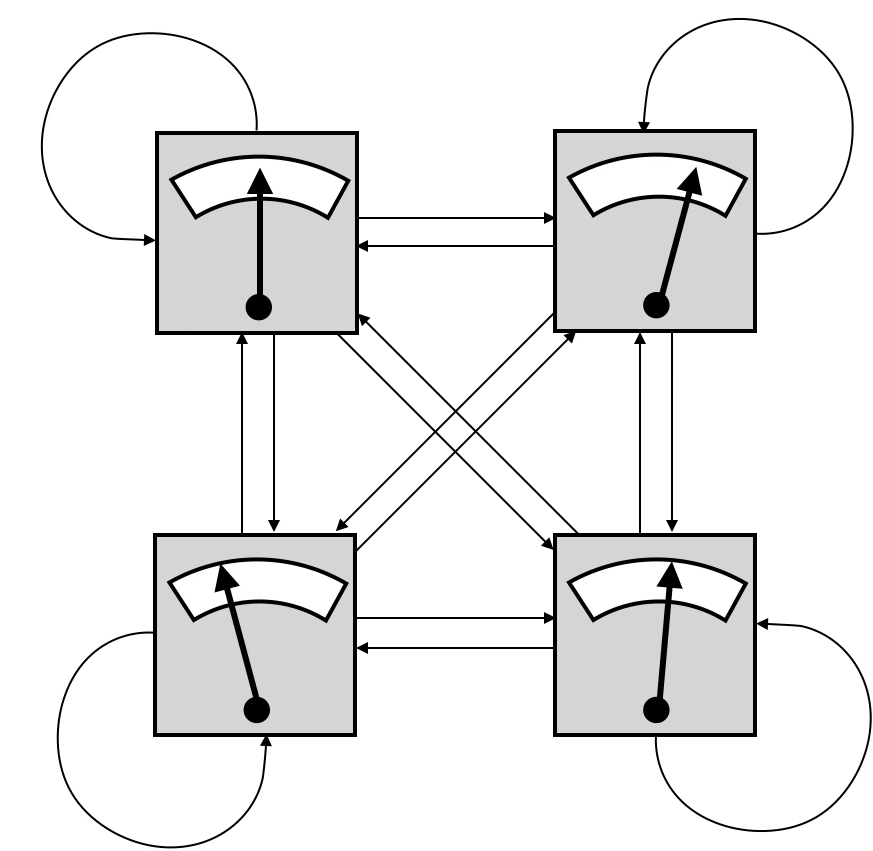
図1: ホメオスタットの構成
「ホメオスタットは四つのユニットから構成されている(図1)。それぞれが他の三つのユニットからの入力(と自分からのネガティブ・フィードバック入力)を受けて、これらの入力の重み付き合計が出力となる。この出力値が針で表示されている。それぞれの入力の重みと出力を調節できるようになっている。
この重みの調整がうまく行かないと、針は振り切れてしまう。しかし重みをうまく調整すると、すべての針の位置が中心に来て(適正値を指す)、システムが安定な状態を維持できる。しかもこの安定性はいったん成立すれば、どれか一つの出力を多少いじったとしても四つの針は適正な値のままでありつづける。このような自己修復性のことをアシュビーは超安定性(ultra-stability)と呼んだ。」(本書 p.63-64)
これは現在の視点からは、4つのユニットが全結合しているボルツマンマシンと同じ構造であると言える。しかしホメオスタットはボルツマンマシンと異なり、学習則を持っていない。このためホメオスタットは、安定でない状態になると重みをランダム化する操作を繰り返して、超安定性を確立できるまでその操作を繰り返す。それはまるで現在のスマホゲーでの「リセマラ」と同じ作業だ。
ホメオスタットの定式化
このブログ記事では、ホメオスタットの挙動を再現してみる。(参考文献は最後尾にあり)
ユニット $1,2,3,4$ それぞれの出力を $x_1(t), x_2(t), x_3(t), x_4(t)$ とする。このときそれぞれの出力は以下の微分方程式に従う。
$$ \begin{aligned} \frac{d^2 x_1(t)}{dt^2} &= h(a_{11} x_1(t) + a_{12} x_2(t) + a_{13} x_3(t) + a_{14} x_4(t)) - j \frac{d x_1(t)}{dt}\\ \frac{d^2 x_2(t)}{dt^2} &= h(a_{21} x_1(t) + a_{22} x_2(t) + a_{23} x_3(t) + a_{24} x_4(t)) - j \frac{d x_2(t)}{dt}\\ \frac{d^2 x_3(t)}{dt^2} &= h(a_{31} x_1(t) + a_{32} x_2(t) + a_{33} x_3(t) + a_{34} x_4(t)) - j \frac{d x_3(t)}{dt}\\ \frac{d^2 x_4(t)}{dt^2} &= h(a_{41} x_1(t) + a_{42} x_2(t) + a_{43} x_3(t) + a_{44} x_4(t)) - j \frac{d x_4(t)}{dt} &\qquad(1) \end{aligned} $$
ここで、$a_{11}, a_{12},...$ はそれぞれのユニット間の重みを表す。たとえば $a_{12}$ ならユニット$2$ からユニット$1$ への重みを表す。つまり右辺の第一項は、自分と他のユニットのすべての出力を重みを付けて足し合わせた入力を表している。
$h$ はこのような入力の評価を表す。ここでは定数で $1$ とする。(現在の人工ニューラルネットワークでは、$h$ の部分は活性化関数に該当する。活性化関数はReLUのように非線形性があるのだが、ホメオスタットでは線形和になっている。)
$j$ の入った項は、出力を示す針の粘性を反映している。ホメオスタットの針は水の上に浮かんでいて、入力に比例した磁石に反応して動く。このようなハードウェア的側面が考慮されている。ここでは定数で $0.5$ とする。
ホメオスタットの挙動
このように微分方程式で表現することができれば、初期値さえ決定してやればその挙動を図示することができる。ここでは微分方程式の数値計算のためにmatlabのode45関数を用いている(4次のルンゲ・クッタ法)。githubにある homeostat4.m を動かすと以下の図ができる。
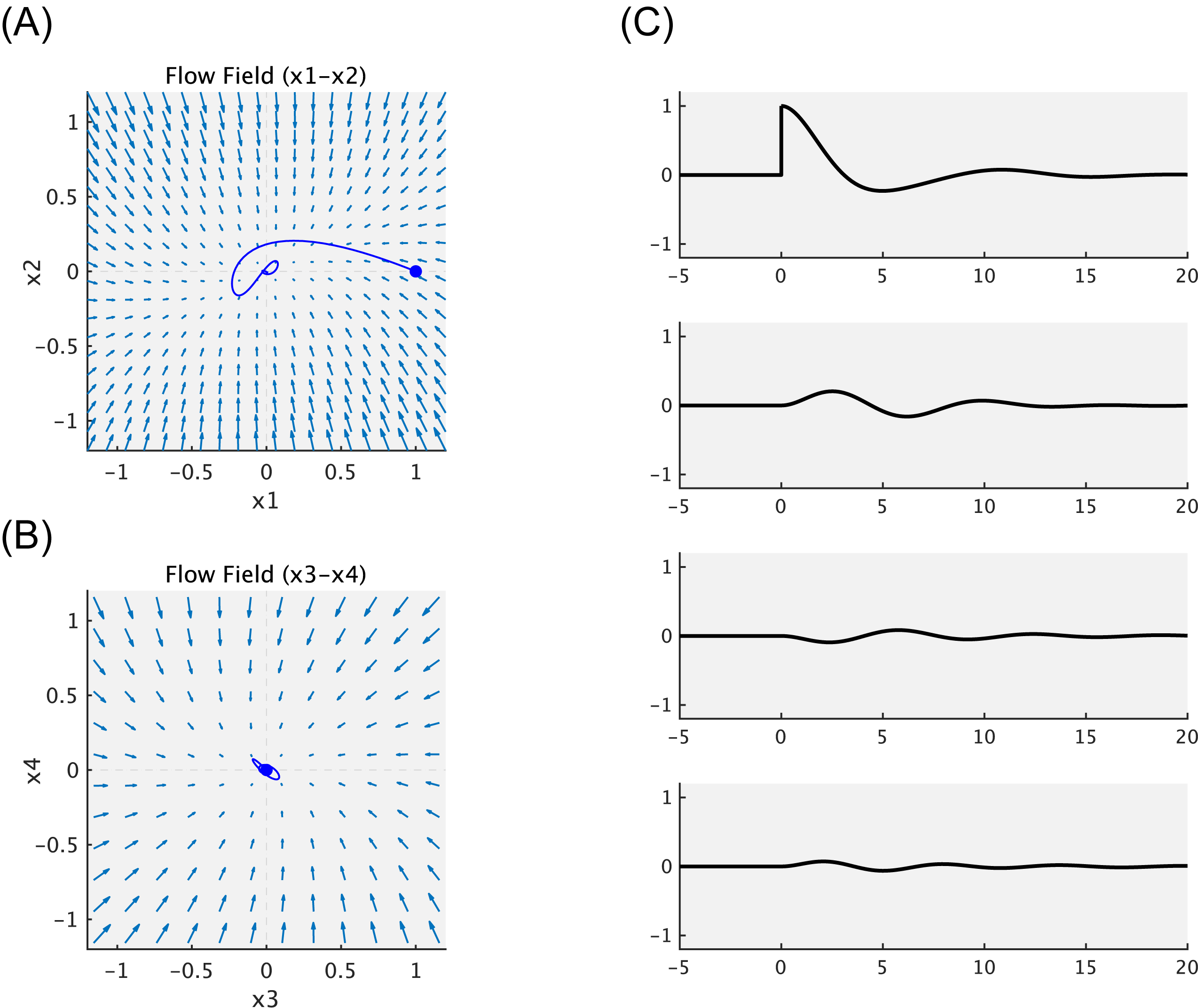
図2: ホメオスタットの挙動
まず図2の左側(A,B)はflow fieldを表している。これはネットワークの重み $a_{ji}$ と定数 $h,j$ によって決まる。Flow fieldは実際には4次元だが、ここでは $x_1 - x_2$ と $x_3 - x_4$ の2つの平面についてだけ表示してある。Flow fieldを見るだけで、初期値をどこにおいても、$0$ に収束することが予想つく。
じっさいにユニット1-4について初期値 $[0,0,0,0]$ を設定すると、ホメオスタットの出力は $[0,0,0,0]$ のまま変動しない。(図2(C)の横軸-5-0(秒)の部分。)
そこで時点 $0$ のところでホメオスタットのユニット1の出力を強制的に $1$ に変更してやる。するとユニット1は速やかに出力値が $0$ へと戻る。このときユニット2,3,4の出力も多少揺れているのがわかる。このようにして、このホメオスタットでは超安定性を達成できているいることがわかる。
ふたたび図2(A),(B)に戻ると、時点 $0$ のところでユニット1の出力を強制的に $1$ に変更したことが青丸で示してある。出力値は $0$ へと戻ってゆくのだが、それは一直線ではない。Flow fieldの向きに従って、多少揺れながら戻っている。
本書では図2を参照しながら「たとえばドカ食いをして血糖値スパイクがおきた状態(ユニット1)でも、健康であるならば、ただちに適正な生理状態が回復できることを示している。」(p.65-66)と書いている。お察しのとおり、この文章は「ドカ食いダイスキ! もちづきさん」を想定していた。初稿は「たとえばドカ食いをして「至った」状態でも」と書いたのだが、後年通じなくなるなと思って、文章を変えたのだった。
ホメオスタットの安定条件
ここで示した例ではホメオスタットは超安定性を達成できている。これはあらかじめそのような重みを選んでいたからだ。この安定条件を見つけるためには、ここまで書いたような、数値解析によって微分方程式の挙動を調べる方法では足りない。解析的な手法が必要となる。
ホメオスタットを定式化した $(1)$ は連立微分方程式になっているので、解析的に解くことができる。それによってどういう重みのときに超安定が達成できるかを調べることができる。
まず、連立方程式 $(1)$ を行列表現に書き換える。
$$ \begin{aligned} \frac{d^2}{dt^2} \begin{bmatrix} x_1(t) \\ x_2(t) \\ x_3(t) \\ x_4(t) \end{bmatrix} &= h \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix} \begin{bmatrix} x_1(t) \\ x_2(t) \\ x_3(t) \\ x_4(t) \end{bmatrix} -j\frac{d}{dt} \begin{bmatrix} x_1(t) \\ x_2(t) \\ x_3(t) \\ x_4(t) \end{bmatrix} \end{aligned} $$
ここで、$x=\begin{bmatrix}x_1(t) & x_2(t) & x_3(t) & x_4(t)\end{bmatrix}^{tr}$ 、 $x' = \frac{d}{dt}x$ 、 $x'' = \frac{d^2}{dt^2}x$
$$ \begin{aligned} A &= h \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix} \end{aligned} $$
とすると以下のように整理できる。
$$ \begin{aligned} x'' & = A x - j x' \end{aligned} $$
同次微分方程式 $x'' + jx' - Ax = 0$ を解くために、$x = v e^{st}$ の形の解を仮定する。ここで $v$ は定数ベクトル、$s$ は複素数のベクトル。
$x'' + jx' - Ax = 0$ に $x = v e^{st}$ を代入すると、
$$ \begin{aligned} &s^2 v e^{st} + j s v e^{st} - A v e^{st} = 0\\ &(s^2I + jsI - A) v e^{st} = 0\\ &s^2 I + jsI - A = 0 \end{aligned} $$
ここで $I$ は単位行列。この式が非自明な解を持つためには、行列式がゼロでなければならない。
$$ \begin{aligned} det(s^2 I + jsI - A) &= 0 \end{aligned} $$
これが特性方程式。この特性方程式の解 $s$ (複素数)の実部がすべて負であるときに収束する。こうしてホメオスタットがどういうときに超安定(収束)を確立し、どういうときに発散するかが計算できる。
しかしこの計算は4つのユニットの場合でさえ非常に複雑であるので、上記のコードではGeminiに安定条件を出してもらって、それを重み $A = {a_{ji}}$ に採用している。
ホメオスタットのその後
「ホメオスタットの挙動を見るかぎり、これは単なる生体恒常性(ホメオスタシス)のモデルに見えるかもしれない。しかしアシュビーはこれを著書『頭脳への設計』において「考える機械」のプロトタイプとして喧伝した。つまりアシュビーにとって、人工の脳をデザインするとは、チューリングマシンのような入力、出力、その変換関数で決まる制御システムを作ることよりはむしろ、外部からの擾乱に「能動的に」抵抗してそのシステムの状態を保つ側面のほうが重要だったようだ。」(本書p.66)
「アシュビーはその後ホメオスタットの大型化を目指したが、安定性を確立させることができなかった。現在の知識から言えば、うまくいかなかった理由は力学系の理論から明らかだった。というのもホメオスタットのユニットは入力の線形和によって駆動される、線形なシステムだったからだ。」(本書p.67)
本書ではこのように書いたのだが、その意味はこのブログ記事の説明からだいぶ明らかになっただろう。超安定性を確立するとは、特性方程式の安定解を見つけることだ。4つのユニットであれば、重みのランダム化(リセットマラソン)でそのような重みを見つけることはできたかもしれない。ユニット数を増やしたらランダムサーチという方法が立ち行かなくなることがわかる。
アシュビーはホメオスタットをスケールアップすることで、考える機械を作ることを目指していたのだが、このプロジェクトは成功しなかった。ではホメオスタットは無駄な試みだったのかというと、そんなことはない。ウィーナーによる評価、ディパオロたちによる再評価、このあたりについては本書をぜひ読んでみてほしい。
参考文献
- William Ross Ashby (1952) Design for a Brain, Chapman & Hall. (邦訳:『頭脳への設計―知性と生命の起源』山田坂仁ほか訳、宇野書店、1967年)
- Franchi S. (2013) Homeostats for the 21st century? Simulating Ashby simulating the brain. Constructivist Foundations 9(1): 93–101. http://constructivist.info/9/1/093
- Battle, S. (2015). Ashby’s Mobile Homeostat. In: Headleand, C., Teahan, W., Ap Cenydd, L. (eds) Artificial Life and Intelligent Agents. ALIA 2014. Communications in Computer and Information Science, vol 519. Springer, Cham. https://doi.org/10.1007/978-3-319-18084-7_9
- / ツイートする
- / 投稿日: 2025年06月07日
- / カテゴリー: [吉田+田口「行為する意識: エナクティヴィズム入門」]
- / Edit(管理者用)
お勧めエントリ
- 細胞外電極はなにを見ているか(1) 20080727 (2) リニューアル版 20081107
- 総説 長期記憶の脳内メカニズム 20100909
- 駒場講義2013 「意識の科学的研究 - 盲視を起点に」20130626
- 駒場講義2012レジメ 意識と注意の脳内メカニズム(1) 注意 20121010 (2) 意識 20121011
- 視覚、注意、言語で3*2の背側、腹側経路説 20140119
- 脳科学辞典の項目書いた 「盲視」 20130407
- 脳科学辞典の項目書いた 「気づき」 20130228
- 脳科学辞典の項目書いた 「サリエンシー」 20121224
- 脳科学辞典の項目書いた 「マイクロサッケード」 20121227
- 盲視でおこる「なにかあるかんじ」 20110126
- DKL色空間についてまとめ 20090113
- 科学基礎論学会 秋の研究例会 ワークショップ「意識の神経科学と神経現象学」レジメ 20131102
- ギャラガー&ザハヴィ『現象学的な心』合評会レジメ 20130628
- Marrのrepresentationとprocessをベイトソン流に解釈する (1) 20100317 (2) 20100317
- 半側空間無視と同名半盲とは区別できるか?(1) 20080220 (2) 半側空間無視の原因部位は? 20080221
- MarrのVisionの最初と最後だけを読む 20071213