pooneilの脳科学論文コメント

■ Marrのrepresentationとprocessをベイトソン流に解釈する(2)

前回からの続きです。では、これを使って、以前書いたMarrの3x2の静的構造(三つのレベル * process/representation)を、弁証法的にメタに上っていけるような構造として捉え直すことができるんではないか、なんてことをわたしは考えた。まだかなり生煮えなアイデアなのだけれど、書いてみましょう。書いてると整理できてくる。

---

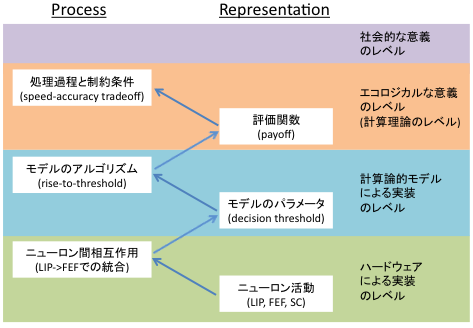
例として、decision taskをやっているときのLIP-FEF-SCニューロンの活動をrise-to-thresholdモデルを使ってモデル化する状況を考えてみる。われわれはLIP-FEF-SCニューロンの活動を記録する。単一ニューロンかもしれないし、集団かもしれないし、LFPかもしれない。また、発火頻度を扱ってるかもしれないし、correlationやcoherenceをあつかっているかもしれない。どうあれ、これらは観察者の我々から見た情報表現だ。

ShadlenやSchallの仕事とかで、LIPやFEFのニューロンはdecisionが済んでサッカードをする直前にある一定の発火頻度まで上がることがわかっている。たとえば、reaction timeが短いときはその発火頻度まで上がってくるのにかかる時間が短かったりする。こういうのを使ってneural correlate of decisionだ、みたいな主張をする。

しかし、常々思っていたのだけれど、こういうときのthresholdの実体とはなんだろうか？ つまり、計算論的モデルでthresholdというパラメータを設定したとして、これのneural correlate of thresholdのようなものはありうるのだろうか？ どこでサッカードが始まるかの発火頻度の値のことだから、やっぱりFEF/LIPニューロンの活動でしょ、というのが大方の意見だと思うのだけど、なんか変だとずっと思ってた。これがいまの図式だともっとうまく説明できる。

つまり、decision thresholdの変化というのは、(たとえば)LIPニューロンからの入力がFEFニューロンで統合されて発火として出力されるときの変換関数(=process)の形の変化のことだ。だから、decision threshold (representation)を直接ニューロン活動(representation)で説明しようとするのはクラスからクラスのクラスへ飛ぶような誤りをしているのであって、かならずやprocessを介して考えないと見誤る。変換関数(process)じたいはもちろん実体(representation)を持っていて、膜電位レベルとかそういうものによって決まっている。でもthresholdの調節はあるニューロンの応答特性を他の入力によって変える(shunting inhibitionでもtonicなinhibitionでもup-state-down stateでも)というようなprocessとして説明しないと、充分な説明にならない。

このようにして決められたdecision thresholdがパラメータとなっているrise-to-thresholdモデルというアルゴリズムがあって、それは計算論レベルでは何らかの評価関数を最適化している。いまの場合だったらreward rate (=payoff: しかも時間あたりの労力を加味した上での)だろう。そうしてそれはspeed-accuracy tradeoffによって拘束されている。拘束されているという表現からもわかるように、ここはエコロジカルな意義によって決定づけられている。Marrの三つのレベルではあくまで工学的な捉え方からこのレベルを「計算論のレベル」と読んだけど、我々生き物がembodiedしたcognitionを行うときの階層として捉え直すならば、「エコロジカルな意義のレベル」と呼んでもいいんじゃないかと思う。

たぶん、この階段はさらに上に上ることができて、社会的な意義とかのところまで行ける。単一のcognition, actionでここまで考える必要がある機会は少ないかもしれない。でも、いろんなcognition, actionが協調した上でなにかを最適化するという場面(複数の行動の連携、他者の行動との協調など)ではこのメタなレベルの出番が出てくるのではないか。

ともあれ、上の階層に行くほどにそんなにバリエーションは多くなくなる。MarrのVisionでの計算論レベルでの目標というのも「外界の画像から、不適切な情報によって乱されない、観察者にとって有用な記述を作り出す」というところに収束する。「観察者にとって有用な記述」ってのはMarrの表現だけど、もろにエコロジカルな意義そのものだ。

いまの図では実験データから抽象する側に矢印が書いてあるけど、もちろん実際の作業ではこのレベルを上ったり降りたりしながらモデルがrefineされてゆく。

たとえば、rise-to-threshold modelと書いたけどその中にはさらにいろんな実装があって、複数のdecision signalがthresholdまで競争するrace modelやらdecision signalの差分だけを評価して決めるモデル(Ratcliff modelはこっち)などがある。これらを選択するときには、これらのモデルで使われるパラメータのどっち(差なのか絶対値なのか)が脳内のプロセス作り出されているか、という風に決めてやるのが一番強い。この意味でいわゆるneurobiological model (生理学的データに整合性のある挙動を示すように作った神経回路モデル)の重要性がある。心理物理だけで、つまり、行動とモデルとの対応付けだけでは脳での実装が考えられていないから、充分な拘束条件を与えないままに問題を解いていることになる。それでも解けてしまう問題もあるのだろうけど。(そもそも元の図式にも「行動」がないというのが変な話だ。正確に言うと、中間のレベルは心理物理によって明らかにすることができる、という言い方で取り込まれてはいるのだけれど。)

いわゆるneurobiological model、たとえばの例ではDoug Munozのmoving hill hypothesisとかは計算論的視点がないので(なにを最適化しているかということに対する答えを持っていない)、Marrが言う意味での計算論モデルにはなっていない。だからといって軽視する必要はなくて、そのようなneurobiological modelというのはある意味、ハードウェア実装レベルでのprocessについての記述となっていると言えるかもしれない。(たとえそんなに精密なものではなかったとしても。) あ、いま書いてて気づいたことだけど、これは意義深いかもしれない。ハードウェア実装レベルのprocessを記述するというのは難しいことであるけれど、プリミティブなものはすでにある。Sommer-Wurtzのcorollary dischargeだって、Naya-Yoshida-Miyashitaのbackward spreadingだって、fMRIで出てくるfunctional connectiityだって、脳間のinteractionを見ているものはみんなそういう方向を目指している。

この図式はほかの場面でも使える。Saliency mapでのwinner-take-allがどのようなモデルのパラメータで表現されるものを統合していて、それのneural correlateを考えるためにはどんなニューロン間の相互作用を考えるべきなのか、というふうに考えていけばよい。

あと、「ニューロン間相互作用」というのはもちろん、シナプス伝達によるdendriteでの統合だけを考える必要はなくて、LFPレベルの電場が揺れて同期発火するとかそのあたりも併せて考えればよい。ニューロン活動のレベルと、もっとglobalなstateと、計算論的問題とをどうつなげればよいかを考える際にも、いまの図式は役立つはずだ。

いま書いていることをスローガン的に言えば、システムニューロサイエンスをneural correlate探しの博物学(representation)から計算論的アルゴリズム解明のためのモデル化(process)へ移行させよう、ということになる。こういう言い方ならたぶん多くの人が同意してくれると思う。いま作った図式はそのムーブメントを進めていく上でのフレームワークとなりうるのではないだろうか。

たぶんいろいろと疑問が出ると思う。はたしてこの階段のステップは飛び越せないのだろうか？ じっさい、これまでの多くのシステムニューロサイエンスの仕事はこのステップをいくつか飛ばしているように思う。たぶん、そのときにはいろんなimplicitな過程をおいて飛ばしている。そこにはtrivialなものもあれば、見逃せないものもあるだろう。なんにしろ、具体例を持ってきて考えることができそうだ。

たとえば、decodingとかneural correlateとかはどちらかというと確信犯的に途中のステップを飛ばしている。Perceptual decisionの結果がMTの活動と相関しているのは確かで、それを直接結びつけることができたのはすごいことだけど、MTの活動自体はretina->LGN->V1->MTと順番に統合が進んでいく中でのconnectionist model的に言えば中間表現に過ぎない(注)。だから、それがどうしてperceptual decisionの結果と一致するかを「相関」ではなくて操作可能な「精密科学」として解明してゆくためにはこの図式にあるようなステップを上り下りする必要があるのではないだろうか。(ここをちゃんと突き詰めると、neural correlate of XX批判になる。Opinion論文を作るときには喧嘩を売ることが重要なので、ここを研ぎ澄ませる意義はある。それはまた今度。)

(注：そこにexplicitなrepresentationがある必然性はない。なのになぜかそうなっている。これ自体はsparse codingの機能的意義として考える必要がある。)

たぶん、process-representationの分け方はハードウェアによる実装のレベルではより重要だ、というのも、測定系の限界ゆえに、representationを調べられるのはほんの一部分だけだし、それを使ってprocessを明らかにするということはまだ方法論的に非常に難しい。いまのBMIやoptogeneticsが切り開こうとしているのはこの領域だ。

一方で、計算論のレベルや計算論モデルの実装のレベルなどではこのprocess-representationを分けて取り扱うということ自体はそんなにcriticalではない。両者は同時に行うことができる。(Speed-accuracy tradeoffを考えずにpayoffを評価してもあまり意味がない。) それでも、Ullman-Koch 1985でアルゴリズムとしてのsaliency mapが提唱されてからItti-Koch 1998でそれを計算モデルとして実装してそれぞれのパラメータを決めて動くようにするまでには10年以上の時間が必要だった。だから、たぶん必ずしもtrivialな問題なわけではない。(ちなみにそれをさらに脳損傷モデルによって、そのモデルパラメータの挙動を調べることで、このアルゴリズムをrefineする、つまりハードウェア実装レベルと繋げようというのがまさにいま私がやっていることだったりする。)

Marrの表現では二番目のレベルは「表象とアルゴリズム」のレベルだが、表象自体はほかのレベルにもあるので、言い方を変えてみた。計算論的なレベルをより具体的にどういうアルゴリズムでimplementeするか、というのが本質だと思う。

もはや大学院講義で話すべきネタではなくなっている。こんなことが頭の中をぐるぐる回っていて、宿題はどんどん拡散してゆく。まあ、得てしてこういうときがいちばん面白いこと考えつくんで、こうやって書き付けておく。どんどん加筆していったので、前提とかの順番はひっくり返ってるかも。

あとはいくつか文脈的につなげられなかったメモを落ち穂拾い。

Hebbのorganization of behaviorからcovariance ruleだけでなくcell assemblyが再評価されたように、Marrも三つのレベルの話だけでなく、process-representationの軸の方も見直したらいいのではないかと考えてる。

ベイトソンは数学を使えなかったけど、いろんなところに構造とその相互関係を見いだした構造主義者としてとらえることができる。レヴィ・ストロースの構造主義的人類学の先駆者と言えるわけだし。でもって、ベイトソンはそういうブーツストラップを考えていたんだから、静的な構造主義ではなくて、「構造と力」というところまでたどり着いていたとは言えないの？ 「構造と力」でメルロ・ポンティが予定調和と批判されるからには、たぶんわたしの誤読なんだろうけど。