« Saccadic suppression: 藤田昌彦先生からのコメント | 最新のページに戻る | 生理研研究会 オンライン参加申し込みを開始しました »
■ 細胞外電極はなにを見ているか
夏が来れば思い出す・・・のは生理研トレーニングコースの準備です。ここ数年は当研究室では、「麻酔下動物での急性電気生理実験」というタイトルで、細胞外電極を使って麻酔下ratからLFPを記録して、視覚刺激に対する上丘の応答をみたり、ひげ刺激に対するbarrel cortexの応答を見るということをやっております。でもって、LFPで記録しているものがなにか、ということを毎年わたしがちょこっと講義しています。
問題なのは、適切な教科書がないということです。この問題については以前にも書きました(20050817および20050818)。細胞内電極やパッチクランプ用電極を使った細胞内電位の記録に関しては、ホジキン・ハックスレーあたりについて書いている生理学の教科書を読むことから始めて、"the axon guide"あたりまで読んでおけばだいたい入門できるかと思うのですが、細胞外電極を使った細胞外電位の記録に関しては良いものがありません。わたしが日々行っている、行動中のnhpのsingle-unit recordingがまさに、タングステン製の細胞外電極を使って、単一細胞のaction potentialを細胞外電位から記録しているものなのですから、よろしくない事態です。また、multiunit recordingやLFPなどが今後BMIなどの応用の面からさらに重要になってくるであろうことを考えると、このへんの基礎をきっちり押さえておくことは大切なことだと思います。
それで、今年もトレーニングコースの時期がやってきましたので、いそいそと準備しているのですが、しょうがないので自分でいろいろ調べて作ってみました。まだ自分で納得いけてないところがあるのでここで皆様の意見を聞きたい、というわけです。物理をわかっている方ぜひご協力お願いします。それではここから:
追記081108:リニューアル版のエントリを作りました。そちらもご覧ください。
(印刷用にPDFファイルを作りました。ファイルをダウンロード。数式のフォントがきれいでないのでhtmlを印刷した方がよいかも。)
(追記:いろいろ書き直してます。オリジナルのエントリはpdfファイルとして保管しておきます。)
[まとめ]
- 細胞外電極はなにを計測している? - 細胞膜を流れる電流。
- 細胞膜の間を流れる電流の正体は? - シナプス電流とaction potential。
- 低周波成分はLFPと呼ばれ、シナプス電流を反映している。
- 高周波成分はMUAと呼ばれ、action potentialを反映している。
- LFPは必ずしも電極の近傍で起こっている電流を反映しているとは限らない。離れたところで起こっている電流を反映している可能性がある。
- CSD解析では、さまざまな深さから記録した細胞外電位から、細胞膜の間を流れる電流の発生位置を推定する。
- 細胞外電極が神経細胞の非常に近傍にあるとき(<50µm)には、単一の神経細胞からの活動電位を反映したsingle-unitを記録することができる。
[細胞外電極はなにを計測している?]
ひとことで言えば、電極近傍の細胞膜を流れる電流を計測している。細胞膜電位ではない点に注意。
もっと正確に言うために、細胞内電極での記録と比較してみよう。図1(1)にあるように、細胞内電極は細胞内の電位Vintと無限遠に置いた不関電極での電位V∞との差を計測している。これはけっきょくのところ、細胞膜間の電位差(細胞膜電位)を計測していることになる。
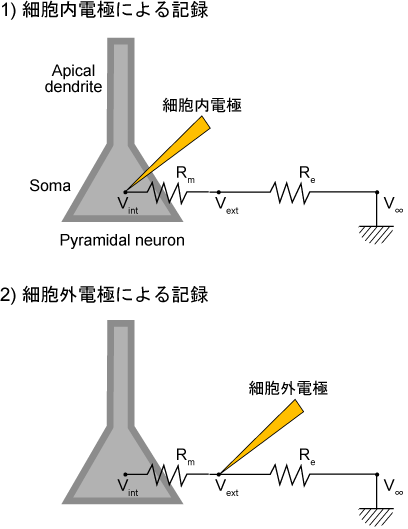
図1 細胞内電極(1)と細胞外電極(2)の記録の違い
Vint - V∞ ~= Vint - Vext (Rm >> Rextより、) = Vm ---(1)
細胞膜の両端にかかっている電位を計測しているという意味で、これはテスターである部分の電位差を測るのとまったく同じである。
一方で、細胞外電極(図1(2))は細胞間隙に置いた細胞外電極での電位Vextと無限遠に置いた不関電極V∞とのあいだの電位差(細胞外電位)を測定している。
Vext - V∞ ---(2)
しかし、ここで測定されたReの両端の電位差そのものには生理学的な意味がない。つまり、テスターでの計測をイメージするとおかしなことになる。
じつは、細胞外電極で記録される電位差は、細胞間隙に置いた細胞外電極の周りで起こった電流によって出来た電場を反映しているのだ。
そして、重ね合わせの原理から、細胞外電位は近傍で細胞膜の間を流れる電流量による電位変化の足し算である。電流の発生源から電極までの距離に反比例して弱くなる。数式で書くと、
Vext = R/(4*pi)*Σ(Ij / rj) ---(3)
ただし、Vextは細胞外電極で測定された電位、Rは細胞間隙の抵抗でだいたい200-300ohm/cm。Ijはある場所jで流れた電流の大きさ、rjは場所jから細胞外電極までの距離。Σはすべての電流源jでの総和。(Nunez and Srinivasan(2006)より)
だから、無限遠に置いた不関電極では、r=∞でVext = V∞ = 0となり、電流の影響が全くないところでの電位を計測していることになる。不関電極との差分を計測することで細胞外電極は電流の影響を計測していると言える。
上記の(3)式についてもうすこしくわしく書くと、クーロンの定理から
E(r) = R/(4*pi)*I/r2 ---(4)電流Iがあると、r離れた部分に電場E(r)ができる。後述の通り、電場E(r)はベクトル場。
電場ができるとそこには電位が生まれる。つまり、
E(x,y,z) = -grad(V(x,y,z)) ---(5)ある地点(x,y,z)の細胞外電位V(スカラー場)の勾配gradientを取るとその地点の電場E(ベクトル場)になる、というふうに電位が定義される。
以上の(4)(5)からEとqを消去して、sourceごとに足し併せると(3)式になる。
ここでつかうべき(4)の式はcharge sourceの式ではなくてcurrent sourceの式であるべきだからこれで良いと思うのだけれど、Nunez and Srinivasan(2006)には記載がない...
[細胞膜の間を流れる電流の正体は?]
では、「細胞膜の間を流れる電流」とはいったいなにか。主に二つのものが考えられる。
- シナプス電流(EPSCとIPSC)。
- Action potential(に伴ったNa,Ca流入、K流出)。
これらはべつべつの周波数帯域と空間解像度を持っている。よって同じ電極からフィルタを使って両方の活動を分離することができる。
Local field potential (LFP):
- 周波数成分 1Hz-300Hzあたり
- 主に電極近傍のsynaptic current (EPSC, IPSC)による。
- synaptic currentはamplitudeは小さいが、time courseが長いので、近くの入力のspatial summationが起こる。
- 電極先端から0.5-3mm程度の範囲のシナプス電流が寄与する。(Logothetis (2008)より孫引き。) 電極の抵抗に依存する。
- あくまでシナプスの位置が重要であり、電極先端に細胞体があることを保証しない。このへんについては「Volume conduction、sinkとsource」にて後述。
Multi unit activity (MUA):
- 周波数成分 300Hz-5KHzあたり
- 電極近傍のaction potential による。
- action potentialはamplitudeは大きいが、time courseが短いので、近くの入力と<1msオーダーで同期しない限り、キャンセルアウトする。
- 電極先端から50-350µm程度の範囲のニューロンの活動電位が寄与する。(Logothetis (2008)より孫引き。) 電極の抵抗に依存する。
つまり、ざっくり言えば、一つの細胞外電極から記録される信号を周波数で分けることによって、LFPは入力(=シナプス電流)、MUAは出力(=action potential)、と違ったものを分けて見ることができる。
(なお、さいきんでは、action potentialのあとで見られるafterhyperpolarizationなどの遅いnon-synapticな成分がLFPに効いていることがわかってきている。けれども、それを入門のときに言うと混乱するので言わない。)
[Volume conduction、sinkとsource]
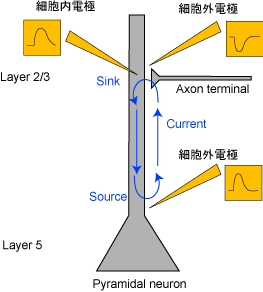
図2 興奮性シナプス電流
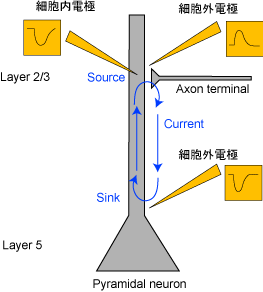
図3 抑制性シナプス電流
上の段で「細胞膜の間を流れる電流」には二つある、と書いたがそれは正確でない。上記のようなシナプス電流やaction potentialなどでactiveな電流が出来たときには、閉回路を作るためにpassiveな電流も流れる。よって、電極から記録されている現象が電極の近傍で起こっているactiveな電流によるものなのか、それとも離れたところで起こっている電流から作られたpassiveな電流によるものなのかは自明ではない。
たとえば、図2のようにシナプスで興奮性シナプス電流(EPSC)が起こっているとき、dendriteおよびsomaで細胞内電位の上昇が見られるが、細胞外電位はdendriteでは近傍の電流流入を反映した下向きのpotential(sink)が記録されるが、somaではpassiveな電流流出を反映した上向きのpotential(source)が記録される。よって、電極からsourceが記録されたとしても、かならずしも近傍の抑制性シナプス電流(IPSC)を反映しているわけではない。これは図3のように抑制性シナプス電流(IPSC)が起こっているときの図と併せて考えてみればわかる。つまり、下向きの細胞外電位が記録できたとしても、それは近傍での興奮性シナプス電流(EPSC)によるものかもしれないし、離れたところでの抑制性シナプス電流(IPSC)によるものかもしれない。
ともあれ、action potentialやシナプス電流によるイオンの流入流出よるactiveな電流にはpassiveな電流が伴う。これによってsinkとsourceのペアが生まれる。
このsink(吸い込み)とsource(湧き出し)という概念は、電磁気学の教科書で大昔たぶん習った、ラプラスの方程式、ポアソンの方程式で言ってることを数式を使わずに表現したもの。数式を使うと、電極の先端では電荷がないので、
div(grad(Vext)) = 0つまりラプラスの方程式となるが、この方程式を二つの境界条件、つまり、シナプスなどの電流源では
div(grad(Vext)) = -ρ/εポアソンの方程式が成り立つし、無限遠では
Vext = 0が成り立つ、というのを使って解くことで、Vextを計算することができる。
[Current source density (CSD)解析 その1]
上記の(3)の式にあったように、細胞外電極から記録される電位は電極近傍の電流の重み付き加算をしている。よって、一ヶ所の細胞外電位の記録だけではどこで電流流入が起こっているかを正確に推定することはできない。そこでさまざまな深さから細胞外電位を記録したデータをもとにして、電流の発生位置、つまりsinkとsourceの分布を推定する。これがcurrent source density (CSD) analysisだ。
結論だけ書くと、大脳皮質のように層構造を持っている脳部位で、深さ方向z(i) (i=1...n)で記録した細胞外電位をVext(z(i))とすると、それぞれの深さでの電流Im(z(i))は、
Im(z(i)) = -(1/R) * d2Vext(z(i))/dz2
となる(Mitzdorf 1985より)。つまり、深さz方向の軸で2階微分を計算すればよい。ただし、Rは細胞間隙の抵抗で、だいたい200-300ohm/cm。
深さ方向で等間隔に記録をしておけば、2階微分はある深さz(i)での細胞外電位Vext(z(i))とその隣り合った深さの細胞外電位Vext(z(i-1))およびVext(z(i+1))とから計算できる。
Im(z(i)) = -(1/R) * ( Vext(z(i+1)) + Vext(z(i-1)) - 2 * Vext(z(i)) )
よって、等間隔ということが非常にcriticalなので、一本の電極を進めてゆくよりかは等間隔で記録部分が並んでいるミシガン・プローブのタイプの電極を使って記録する方がよい。
くわしく導出仮定を書くと、
連続方程式より、 div(J) = Im ---(1)オームの法則より、
J = (1/R) * E ---(2)(ここでは1/R = σは均一の定数とする。)
前述の電場と電位の関係より、
E = -grad(Vext) ---(3)(2)と(3)よりEを消去すると、
J = -(1/R) * grad(Vext) ---(4)(1)と(4)からJを消去するとポアソンの方程式ができる。
(1/R) * div(grad(Vext)) = -Im ---(5)これをx,y,z成分にばらすと、
(1/R) * (∂2Vext/∂x2 + ∂2Vext/∂y2 + ∂2Vext/∂z2) = -Im ---(6)大脳皮質のように、深さz方向に延びたニューロンがx,y方向で同じように並んだ構造をしているときにはx方向、y方向の2階微分は0になるから、z成分だけが残る。
(1/R) * ∂2Vext/∂z2 = -Im ---(7)(Mitzdorf (1985)より。)
[Current source density (CSD)解析 その2]
CSD解析で得られたImから、ある時間tでの深さ方向のsink-sourceの分布を推定することができる。しかし、上記の通り、このようなsink-sourceのペアは[activeな電流(channel開閉によるイオンの移動)によるもの]と[閉回路を作成するためのpassiveな電流]のどちらに対応するかを一意に決めることはできない。そこで、解剖学から得られた細胞構築のパターンなどを援用することによって、activeな電流の位置を推定する必要がある。
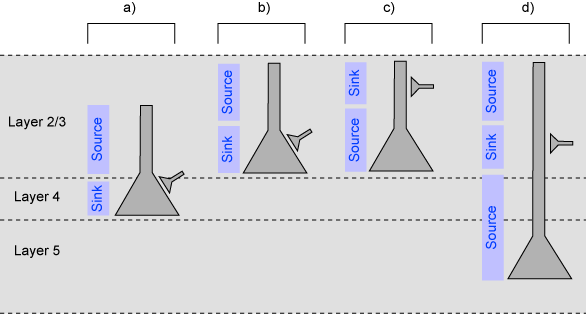
図4 CSD解析
かなり単純化した話だけれども、大脳皮質のおもなpyramidal neuronはlayer 3 (図4b-c)かlayer 5(図4d)にあって、apical dendriteを上に延ばしている。大脳皮質への入力はlayer 4 (図4a)にsomaのあるgranule cellに入力する。また、大脳皮質ではIPSCはあまりfield potentialに寄与していないことがわかっているので、EPSCだけに限る。(海馬とかだとこうはいかない。) また、sink-sourceの分布は細胞体を超えて広がることはない。
これらのことから、a)-d)のそれぞれ左にあるsink-sourceの分布パターンが見られたときには、a)-d)のそれぞれ右にあるようなニューロンへの興奮性シナプス入力が寄与していると推定することができる。
おわかりの通り、かなりざっくりとした推定なので、他の情報、たとえばsliceでの細胞内記録とそのあとのmorphologyの再構成とかと組み合わせていかないといろんなところに落とし穴がある。
このようなテクニックは1970年代後半から実用化した、けっこう古いテクニックではあるけれど、今後のLFPやMUAを使ったBMI研究においてinverse problemを解く際に、生理学的知見を用いたforward modelを作成するにあたって再び重要なテクニックとなるんではないだろうか、というのが私見。
[Single-unitの記録]
もし細胞外電極が神経細胞の非常に近傍にあるとき(<50µm)には、単一のニューロンからの活動電位を反映したsingle-unitを記録することができる。上記のMUAの特殊な例と捉えることができる。私自身はこっちが本業だけど。
教科書とかで見る細胞内電極で記録した細胞膜電位Vmはposiの山が一つで、ゆっくり落ちてくる。いっぽうで、single unitの波形Vextはそれより速くて、だいたいtriphasic。posi-nega-posi。このへんにはHenze et.al.(2000)とかの図を入れておきたい。
Single unitの波形Vextがなんであんな形をしているか。細胞内電極で記録した細胞膜電位Vmと関係づけたい。Henze et.al.(2000)では、
Vext = dVm/dt
時間ドメインでの1階微分としている。ただし、波形の後ろの方はafterhyperpolarizationとかそのへんの影響で、計算からかなりずれる。
[細胞膜電位と細胞外電位との関係の導出] (未完結)
これを導出するためには以下の手順が必要となる。(Gold et.al. (2006)より。) 複雑なのでだいたいNEURON simulatorとかが使われる。なんかもっと簡単な説明があると良いのだけれど。
- まず、Na channel、K channelの開閉によるチャネルコンダクタンスgNa, gKのダイナミクスとそれによる電流INa, IKを計算する。
- この電流によって起こる細胞膜電位Vmの変化をRallのcable方程式から計算する。
- この電流によって起こる細胞外電位Vextの変化をHolt-KochのLSA(line source approximation)によって近似的に計算する。
- 以上を(近似でいいから)解析的に解けばたぶん1階微分であることが示せるはず。
ただ、よくわからないのは、昔の本(Geddes(1972)とか)を読んでると、Lorente de No(1947)とかTasaki (1959)を引いて、2階微分だって書いてあるのがある。Axonでの記録だけど。(正確にはImとVmの関係についてだけど。) Llinas R, Nicholson C (1974)とかだと、Rallのcore conductor modelで近似できるような条件では、
the field potentials in the vicinity of extracellular sources or sinks are proportional to the first derivative of transmembrane voltage with respect to time.
とか書いてある。いっぽうで、excitable membraneでは、Imにはchannelによるcapacitanceの成分が入ってくるので、
the extracellular potential will be proportional to the second derivative of potential with respect to time
とか書いてある。たぶんこのへんを読めばわかるのかな。Lorente de Noまではさかのぼらずに済ませたいのだけれど。
そっか、基本的にはImとVmの関係さえわかればいいのだから、これは細胞外電極に限った話ではないな。Rallのcable方程式で、興奮性シナプスのある場合のバージョンを用いて、ImとVmとの関係の式にしてやればよいのだな。このへんを進めてみることにしよう。
[参考文献]
- Bedard C et.al., (2004) "Modeling extracellular field potentials and the frequency-filtering properties of extracellular space."(pdf) Biophys J. 2004 Mar;86(3):1829-42.
- G. Buzsaki (2006) Rhythms of the Brain: Oxford University Press (のうち、Cycle 4 "Windows on the brain")
- Geddes L.A. (1972) Electrodes and Measurement of Bioelectric Events (Wiley-Interscience, New York).
- Gold C et.al., (2006) "On the origin of the extracellular action potential waveform: A modeling study." J Neurophysiol. 95(5):3113-28.
- Henze, D. et.al., (2000) "Intracellular features predicted by extracellular recordings in the hippocampus in vivo." J Neurophysiol. 84, 390-400.
- Holt, GR (1998) "A Critical Reexamination of Some Assumptions and Implications of Cable Theory in Neurobiology."(pdf) Ph. D. Thesis, California Institute of Technology, Computation and Neural Systems Program
- Holt GR and Koch C. (1999) "Electrical Interactions via the Extracellular Potential Near Cell Bodies". Journal of Computational Neuroscience 6:169-184
- Kandel ER, Schwartz JH, Jessel TM, eds. (2000) "Principles of Neural Science", 4th ed. McGraw-Hill:New York, NY.
- Llinas R, Nicholson C (1974) "Analysis of field potentials in the central nervous system." In: Handbook of EEG and clinical neurophysiology (Stevens CF, ed.), pp. 61-85. Amsterdam: Elsevier.
- Logothetis NK. (2008) "What we can do and what we cannot do with fMRI." Nature 12;453(7197):869-78. (とくにsupplementary informationの"Neural Signals"のセクション)
- Mitzdorf U. (1985) "Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena."(pdf) Physiol Rev. 65(1):37-100.
- Nunez, P. L., & Srinivasan, R. (2006). Electric fields of the brain : The neurophysics of EEG (2nd. ed.). New York : Oxford University Press.
以上です。それで、いろいろまだ不備はあるのですが、なにがいちばん納得いってないかというと、volume conductionでのpassiveなcurrentという概念とdipoleの概念と電場の形成の概念との関係がまだ明確でないと思うのです。Dipoleによる電場の形成はdipoleの周り全体に起きることですが、passiveなcurrentの話は電荷保存の法則に従うもので、細胞膜のかたちによって影響を受け、ニューロンのサイズを超えて分布することはありません。よって二つは別ものなのだけれど、このへんをきっちりと書いている資料というものがあまりなくてわかりにくい。
それから、現在の説明(図2、図3)でもそうなのだけれど、field potentialそのものを使ってsinkとかsourceとか議論するのは正しくないわけです。しかし、われわれが慣れているのはそういう説明で、このへんが混乱の元になっているのではないかと思います。(正しい説明はたぶん、Vext = f(Im)という関係を示したあとすぐに、CSD解析でsource-sinkの推定をしたあとで、それが[activeなイオンの移動による電流]と[passiveな閉回路を作るための電流]のどちらなのかを解剖学的見地などから推測する、というものだと思われ。それはそれでわかりにくいけど。)
また、そうやって考えると、海馬で記録されるfield EPSPというのが、sinkそのものではないものを使って興奮性シナプス伝達を見るという簡便法である、ということも言えるのではないかと思います。
だいたい今年はこんなもんです。つづきはおそらくまた来年の今頃となることでしょう。ではまた。
# Ryohei
簡潔にまとまっていて、とてもよいですねー。PDFにして、講義ノートも公開してください!そういえば、もうすぐ岡崎でセミナーする予定です。お会いしたいですねー。
# pooneilどうもです。Ryoheiさん、Science出版おめでとうございます。
# kazuhi-s講義ノートの公開、いいですね。とりあえず現在のエントリのPDFファイルを作ってリンクしておきます。
内容ですけど、間違いはなかったですか? Vmの1階微分のあたりとか、それからdipoleによる電場の形成とleak currentの関係とか、直せるところがあったらぜひコメントしてください。
岡崎のセミナーは生理研ですか? 分子研ですか? ぜひお会いしましょう!
こんにちは。文献までコンパクトにまとめられていて、とても参考になります。
このエントリについて同僚と議論しているときに話題になったのですが、Single-unitのところではVextが時間微分になっているのに、細胞膜電位と細胞外電位との関係の導出のところでは空間微分になっているのはなぜなのでしょうか。
また一回微分、二階微分、2回微分という書き方が混在しているけど、どれが正しいのかというのも議論になりました。
僕は学生の頃一階微分、二階微分という風に教わりました。
なんだか指摘ばかりで申し訳ありませんが、
E(x,y,z) = -grad(V(x,y,x))
は
E(x,y,z) = -grad(V(x,y,z))
のタイポでしょうか。
# pooneilどうもです。Randy Pausch亡くなってしまいましたね。
# Ryohei>細胞膜電位と細胞外電位との関係の導出のところでは空間微分
しまった、ここでこの式を持ってくるのは間違いでした。とりあえず消しときます。Cable theoryあたりをもうすこし加えるy予定です。
>一階微分、二階微分
「2階微分」で統一しておきました。
>V(x,y,x)
直しておきました。
いちおうHodgkin-HuxleyのPropagationモデルでは∂2Vm/∂z2 ~∂Vm/∂tだから、その式でもよいのかも。というか、H-Hモデルなら、Vext ∝ Σi = -Cm dVm/dtでよい気がします。
# pooneilどうもありがとうございます。Im-Vmの関係だけ考えればよいというのに気がつきました。もうすこし考えてアップデートしてみます。
# Koidarman良い具合にまとまってて読んでて楽しかったです。もとは物理出身なのに、この手の数式をいじって細胞外記録データを記述するということをやったことがありませんでした。さすがです。
その昔、細胞外記録は電磁波を読み取っているんだ、という話を聞いたときに、ためしに電線にパルス電流を流して、それを近傍においた電極で読み取る計測をしてみたことがあります。
パルス波形をいろいろ変更しても、読み取った波形は結局アンプのフィルターのせいでか二相性や三相性の波形となることがわかって、パルス波形を適当にEPSPみたいな形にすると、いつも見ているような神経活動の波形が現れたので、それで納得していました。
# pooneil>ためしに電線にパルス電流を流して、それを近傍においた電極で読み取る計測をしてみた
どうもありがとうございます。さすが、これは物理やってる人の行動ですね。生理学実習でaxonを刺激して、みたいなのをやってるところだとこのへんまで勉強してるんでしょうね。