« 応用問題:海馬sliceのfield EPSP | 最新のページに戻る | 10kg減量しました »
■ DKL色空間についてまとめ
さてさて今度はDKL色空間についていろいろ調べる必要が出てきたので、まとめを作りました。数式がたくさんあるので、エントリでは簡略化してます。くわしくはPDFファイルをどうぞ。こちらから:dkl3.pdf
[要旨]
1) DKL色空間とは、色空間を網膜以降の色処理の三つのチャネル(Luminance, L-M, S-(L+M))の軸によって表現したものです。モニタのRGB値からDKL空間への変換を簡単に説明します。2) Brainard 1996に準拠して、LMS色空間からDKL色空間への変換行列を導出します。3) さいごに、DKL色空間が持つややこしい点について言及します。
[さまざまな色空間]
網膜には三種類の錐体(L-cone, M-cone, S-cone)があって、脳内の色の処理はL-, M-coneの情報を使っているparvocellular pathwayとS-coneの情報を使っているkoniocellular pathwayとに分かれて処理されています。このような状況で便利なのがDKL色空間による色表現です。
網膜から上丘へ直接入力するretinotectal pathwayではS-coneの入力がないと考えられています。そこで、輝度は一定のままに、S-coneへの刺激だけが変化するような刺激(S-cone isolating stimuli)を作ってやれば、S-coneを選択的に刺激できます。もしこのような刺激を処理できないとしたら、そのような情報処理はretinotectal pathwayを介しているという証拠になります。
というわけですが、マイナーすぎて日本語による資料がありません。そこでまとめを作成してみました。わたしは神経生理学者でして、心理物理学者ではありませんので、間違いを指摘していただけるとありがたいです。まさにそれこそがこういう文書を公開した理由なわけでして。
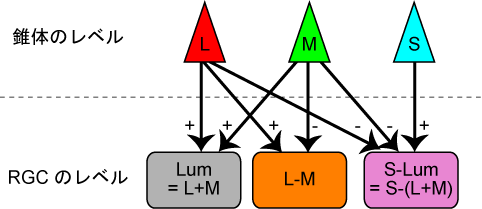
図1 反対色応答
イントロとかは最小限でいきましょう。図1に網膜での反対色応答の形成の図式を作りました。網膜には三種類の錐体(L-cone, M-cone, S-cone)があって、それぞれの足し算引き算によって網膜以降の色処理の三つのチャネル(Luminance, L-M, S-(L+M))ができます。このような三つのチャネルによって、CRTモニタに表示された色がどのように表現されるか、というのがここでの問題です。
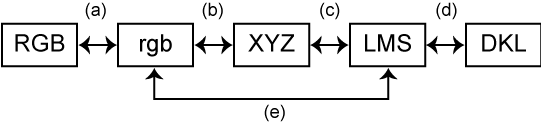
図2 色空間とその変換
図2は色空間とその変換の流れです。
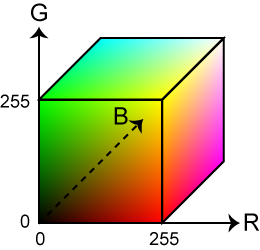
図3 RGB 空間
モニタの刺激はRGBそれぞれ256階調ありますので、3次元で表示することができます(図3)。
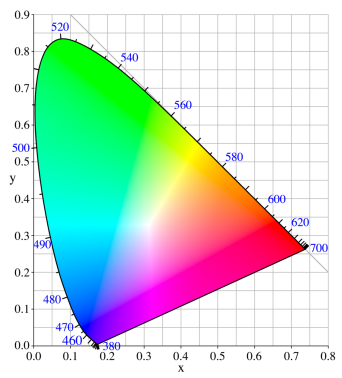
図4 xyY 空間equiluminant plane
XYZ空間はxyY空間に変換できて、x,yで色を表して、Yでluminanceを表します。有名なCIE xyYのequiluminantな平面です(図4)。
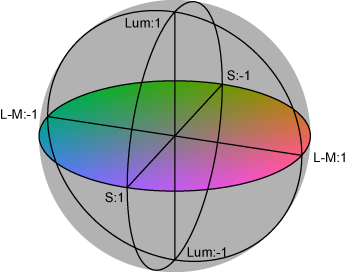
図5 DKL 色空間
LMS色空間はそれぞれのconeでのexcitationの大きさで表現した座標です。LMS色空間は言ってみれば、網膜の錐体のレベルでの色表現です。DKL色空間はさらにもう一段階処理が進んだ、retinal ganglion cell以降での色表現を表したものです(図5)。
じっさいにLGNのニューロンの応答がDKL空間でうまく表現されることが報告されました。この論文がDerrington AM, Krauskopf J, Lennie P (1984) "Chromatic mechanisms in lateral geniculate nucleus of macaque." J Physiol (Lond) 357:241-265.でして、著者の三人の頭文字を取ってDKLと呼ばれるようになりました。それより前に、MacLeod and Robert M. Boynton (1979) "Chromaticity diagram showing cone excitation by stimuli of equal luminance" J. Opt. Soc. Am., Vol. 69, No. 8, p.1183-1186 というのが出版されていまして、こちらはMacLeod-Boynton color spaceと呼ばれます。式の表現の違いはありますが、基本的に同じものです。
[RGB空間からLMS空間への変換]
(省略。くわしくはPDFをどうぞ。)
L-cone, M-cone, S-coneの吸光特性については出版されている論文を使います。いちばん有名なやつは
Smith, V. C. and Pokorny, J. (1975). Spectral sensitivity of the foveal cone photopigments between 400 and 500 nm." Vision Research, 15, 161-171.
ですが、さいきんはもっと新しいので、
Stockman, A., and Sharpe, L. T. (2000). "Spectral sensitivities of the middle- and long-wavelength sensitive cones derived from measurements in observers of known genotype." Vision Research, 40, 1711-1737.
というのがあります。Stockmanのweb siteにデータもあるので、テーブルを自分で入力する必要はありません。これらはhumanのデータです。しかも刺激のサイズによって値が違います。よって、最終的にはなんらか別にpsychophysicalなvalidationの必要性が出てきます。
(省略。くわしくはPDFをどうぞ。)
以上の変換に関しては、Brainard, D. H., Pelli, D.G., and Robson, T. (2002). "Display characterization. In the Encylopedia of Imaging Science and Technology."(pdf file) J. Hornak (ed.), Wiley. 172-188.にくわしい説明があります。この論文はwebからフリーで入手可能です。
さて、このLMS空間からDKL空間への変換(d)を導出するというのがこの文書の本題です。
[LMSからDKLへの変換行列の導出]
つづいて、LMSからDKLへの変換をします。ここの参考文献はBrainard, D. H. (1996). Cone contrast and opponent modulation color spaces."(pdf file) In Kaiser and Boynton, Human Color Vision, 2cd edition, Optical Society of America, Washington, DC.です。この論文はwebからフリーで入手可能です。以下でやってることはこの論文と同じなのですが、計算のステップを省略せずに書いて、確認しながら進めてゆきます。
(省略。くわしくはPDFをどうぞ。)
というわけで、LMSからDKLへの変換は一次変換でした。初めに出てきた図\ref{fig:fig1}での変換(b)-(e)はすべて一次変換です。ですので、PCのモニタで表現できる部分はDKL空間の中では傾いた平行四辺形みたいなものになっています。図\ref{fig:fig3}にあるような球形ではないことに注意。つまり、DKL空間のうちでCRTモニタによって表現できるところは限られていて、normalizationにもよりますが、半径1の球の中で定義できないところもあるし、外で定義できるところもあります。
あと、ここまでゴリゴリやりましたが、じっさいにはbackgroundとしては灰色を設定するでしょう。そうすると、$L_0とM_0とS0$の比を一定にしたままbackgroundの輝度を変えていって、変換行列AとDKL座標の値がどう変わるかを計算してやることができます。そうするとどこかに不動点があるかとかわかるはずですが(Y/2な気がする)、面倒くさいので止めました。
[DKL色空間が持つややこしい点]
前の章で多少言及しましたが、じつはnormalizationの項k_1-k_3は実験の目的によって決まり、一意には定まりません。つまり、pooled cone contrastでのnormalizationは、Lum. L-M. Sの軸での絶対値がperceptualに同等であることを保証しません。もしあるluminanceの刺激とあるS-cone contrastの刺激とを比較したい場合には、detection taskかなんかをやって正答率が同等のところで比較してやらないといけません。このへんの事情については、Brainard 1996でも銘記されています。
また、大元のDKL論文は刺激にCRTモニタを使っていますが、DKL座標のLumimanceの軸の1はMichelson contrastが1になるように設定されています。つまり、DKL = [1,0,0]^tがRGB = [255,255,255]^tだとすると、backgroundがその半分の輝度になるようにしてあります。そしてこのようにして決めたbackgroundからS-lumの軸で提示可能な最大値をS-lum軸の1としています。L-Mについては明示的に書かれてないんですけど。ともあれ、DKLの値はモニタの値に依存します。つまり、モニタのRGBの輝度のバランスによっていくらでも変わるということです。よって、DKL論文だけ引いているような研究だとL-MとSとの絶対値についてはあまり考慮していないと思っておいた方がよいんではないでしょうか。
以上です。謝辞:生理学研究所・感覚認知情報研究部門の鯉田孝和さんにいろいろ教わりました。御礼申し上げます。