[カテゴリー別保管庫] 価値による行動選択 (expected value)
2008年06月24日
■ skyさんからのコメント
Sugrue論文に関するスレッドにskyさんからコメントをいただきました:20060412。どうもありがとうございます。読者の方の目に触れやすくするために以下に転載させていただきました。論文にリンクできるところに関しましてはリンクをつけておきました。(Vaughan & Herrnstein (1981)はPubMedだと見つかりませんでしたが、William Vaughan "Melioration, matching, and maximization" J Exp Anal Behav. 1981 September; 36(2): 141–149.のことでしょうか?)
ついでながらここでVaughan & Herrnstein関連への言及のあるwebサイトを紹介しておきます:
- マッチング行動のメカニズム
- 一般対応法則と意思決定論(pdf)
- 行動経済学と実験経済学(pdf)
さて、それではここからskyさんのコメント:
調べ物をしていたら、このサイトにヒットしました。近年、私が行っていた話題を、こんなところで議論されていたのか、と思って驚いています。あの頃、気付いていれば、議論に参加できたのに、と思っています。
ずいぶん時が経ってしまって申し訳ありませんが、Sugrue(2004)論文に関してここで行われた一連の議論に抜け落ちている点、Soltani & Wang (2006) に対する評価をここで、追加しておこうと思います。
Soltani & Wang (2006) について
彼らのモデルは、状態変数がないQ-leaningをシナプス学習則で実現するモデルとなっており、選択比と強化比の関係は課題と学習パラメータに依存します。したがって、Matching law を実現するモデルでもMeliorationでもありません。逆にその性質を利用してMatching からのずれである undermatching を再現しているかのように見せています。
私は彼らのモデルをQ-leaning及びその亜種をシナプス学習則で実現するモデルとして評価しています。しかし、Matching law とは何の関係もありません。
Matching law を実現するシナプス学習則は、Loewenstein & Seung (2006) が、報酬と行動関連神経活動の間の共分散に比例する "covariance rule" として、一般則を提案しています。
Matching Task について
報酬量を同じにした並列VI-VIスケジュールが、Matching と Maxmizing を区別できる課題ではないことはmmrlさんに指摘されている通りです。また、報酬量を選択肢によって変えた並列VI-VI(Baum & Rachlin 1969)でも、並列VI-VR(Herrnstein & Heyman 1979)でも、DeCarlo(1981)課題でも、Mazur(1985)課題でも、Matching と Maximizing の区別はできますが、区別しやすい課題パラメータを選ぶと、構造的に交互選択がランダム選択より得になりがちで、交互選択をさせないために Change Over Delay もしくはそれに類した、交互選択に対するコストを導入しており、問題を難しくしているばかりか、無理やりMatching Behaviorを出させている印象を与えています。
並列VI-VI,VI-VR,VR-VRの間を連続的につないで包括する競合的採餌課題(Sakai & Fukai 2008)では、交互選択が得にはならないで、Matching と Maximizing が区別できるパラメータはありますが、最適行動がランダム選択でない点は上記課題と共通です。
しかし、Meliorationを提案したVaughan & Herrnstein (1981) は、もっと強力な課題を考案しており、実際、Matching law 及び Melioration を支持する結果を出しています。Vaughan課題は、各選択肢の報酬確率 P(r|a) を、過去の一定期間に被験者がその選択肢 a を取った頻度 N_a に依存して、
P(r|a)=f_a(N_a)
と決める課題です。つまり報酬確率は直前一定期間の選択頻度に応じて変化します。平均獲得報酬は選択頻度のみに依存し、Localな選択順序に依りません。関数 f_a をデザインすることで、最適な選択頻度、Matching law が成り立つ選択頻度を自由に設定できます。Matching を議論するのに適した素晴らしい課題だと思います。しかし、あまりこの課題を使っているのを目にしません。
最近でもMatchingを議論するのに皆、なぜか並列VI-VIを使いがちですが、上述のようにあまり適した課題ではありません。皆さん、Vaughan課題を使いましょう。
強化学習アルゴリズムとの関係について
強化学習アルゴリズムにも、Matching law を示すものがあります(Sakai & Fukai 2008)。Actor-Critic は、課題や学習パラメータに依らず、定常状態でMatching law を示します。ところが、Q-learning は、課題や学習パラメータに依存し、一般にはMatching law を示しません。
- / ツイートする
- / 投稿日: 2008年06月24日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
2006年04月12日
■ Newsome論文のcomputational model
選択行動に関するNewsome論文Science 2004のcomputational modelがXiao-Jing Wangによって提案されています。
JNS "A Biophysically Based Neural Model of Matching Law Behavior: Melioration by Stochastic Synapses" Alireza Soltani and Xiao-Jing Wang
がしげさんのところで詳しく解説されています。つづき期待中。
Xiao-Jing Wangはhosrt-term memoryのときのdelay activityのモデルとかそういうのやってるひとですが、新しいデータに即していろいろやっているようですね。以前もRomoのgradedなdelay activityのモデルやってたよな、と思って探してみたら、Science 2005 ("Flexible Control of Mutual Inhibition: A Neural Model of Two-Interval Discrimination")はRomo and Brodyであって、そのまえのCerebral cortex 2003 ("A Recurrent Network Model of Somatosensory Parametric Working Memory in the Prefrontal Cortex")のほうに入っているらしい。
- / ツイートする
- / 投稿日: 2006年04月12日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
# sky
調べ物をしていたら、このサイトにヒットしました。近年、私が行っていた話題を、こんなところで議論されていたのか、と思って驚いています。あの頃、気付いていれば、議論に参加できたのに、と思っています。
ずいぶん時が経ってしまって申し訳ありませんが、Sugrue(2004)論文に関してここで行われた一連の議論に抜け落ちている点、Soltani & Wang (2006) に対する評価をここで、追加しておこうと思います。
Soltani & Wang (2006) について
彼らのモデルは、状態変数がないQ-leaningをシナプス学習則で実現するモデルとなっており、選択比と強化比の関係は課題と学習パラメータに依存します。したがって、Matching law を実現するモデルでもMeliorationでもありません。逆にその性質を利用してMatching からのずれである undermatching を再現しているかのように見せています。
私は彼らのモデルをQ-leaning及びその亜種をシナプス学習則で実現するモデルとして評価しています。しかし、Matching law とは何の関係もありません。
Matching law を実現するシナプス学習則は、Loewenstein & Seung (2006) が、報酬と行動関連神経活動の間の共分散に比例する "covariance rule" として、一般則を提案しています。
Matching Task について
報酬量を同じにした並列VI-VIスケジュールが、Matching と Maxmizing を区別できる課題ではないことはmmrlさんに指摘されている通りです。また、報酬量を選択肢によって変えた並列VI-VI(Baum & Rachlin 1969)でも、並列VI-VR(Herrnstein & Heyman 1979)でも、DeCarlo(1981)課題でも、Mazur(1985)課題でも、Matching と Maximizing の区別はできますが、区別しやすい課題パラメータを選ぶと、構造的に交互選択がランダム選択より得になりがちで、交互選択をさせないために Change Over Delay もしくはそれに類した、交互選択に対するコストを導入しており、問題を難しくしているばかりか、無理やりMatching Behaviorを出させている印象を与えています。
並列VI-VI,VI-VR,VR-VRの間を連続的につないで包括する競合的採餌課題(Sakai & Fukai 2008)では、交互選択が得にはならないで、Matching と Maximizing が区別できるパラメータはありますが、最適行動がランダム選択でない点は上記課題と共通です。
しかし、Meliorationを提案したVaughan & Herrnstein (1981) は、もっと強力な課題を考案しており、実際、Matching law 及び Melioration を支持する結果を出しています。Vaughan課題は、各選択肢の報酬確率 P(r|a) を、過去の一定期間に被験者がその選択肢 a を取った頻度 N_a に依存して、
P(r|a)=f_a(N_a)
と決める課題です。つまり報酬確率は直前一定期間の選択頻度に応じて変化します。平均獲得報酬は選択頻度のみに依存し、Localな選択順序に依りません。関数 f_a をデザインすることで、最適な選択頻度、Matching law が成り立つ選択頻度を自由に設定できます。Matching を議論するのに適した素晴らしい課題だと思います。しかし、あまりこの課題を使っているのを目にしません。
最近でもMatchingを議論するのに皆、なぜか並列VI-VIを使いがちですが、上述のようにあまり適した課題ではありません。皆さん、Vaughan課題を使いましょう。
強化学習アルゴリズムとの関係について
強化学習アルゴリズムにも、Matching law を示すものがあります(Sakai & Fukai 2008)。Actor-Critic は、課題や学習パラメータに依らず、定常状態でMatching law を示します。ところが、Q-learning は、課題や学習パラメータに依存し、一般にはMatching law を示しません。
コメントどうもありがとうございます。別エントリ(20080624)に転載させていただきましたので。
2006年01月24日
■ Daeyeol Leeからsubjective valueへ
ryasudaさんのNature NeuroscienceがAOPに載った、というのを聞きつけて見に行ったついでで、Daeyeol Leeの論文がAOPに掲載されているのを発見。
"Activity in prefrontal cortex during dynamic selection of action sequences"
んで、まだ読んでないんだけれど、abstの最後の"subjective knowledge of the correct action sequence"を見て、言いたいことを思い出したので一つ。
なんつうか、時間的にlocalなところのreward historyしか使えない状況とか、、もしくはゲーム理論的なシチュエーションでプレーヤー自身が限られた知識(相手側がどう行動するかはうかがい知れない、とか)しか持っていない状況とか、そういうものに対して"subjective"という言葉を使うことがあります。
以前わたしがDorris and Glimcherで問題にしたのは、subjective valueと言っているわりにはexpected utilityではなくてexpected valueを使っているという点でした。しかし、上記の視点が限定されている、という意味でsubjectiveを使ってしまえば、実験者が設定したreward(trial block中で一定な、いわゆるglobalな値)から計算されるvalueではなくて、短い限られたtrialでのreward historyから被験者が推定したrewardから計算されるvalueをsubjective rewardと言ってしまうことも可能です。言い抜けだと思いますけど。
んで、Sugrue and NewsomeのNature Review Neuroscienceでのlocalかglobalか、という議論のところではたしかそういう表現をしていたところがあったような。ということが頭に引っかかっていたんだけれど、思い出したのでメモ。
う、タイトルというかカテゴリ名が長い。このへんまで来ると、カテゴリ名よりはタグ的に扱ったほうが良いんだろうなあ。
- / ツイートする
- / 投稿日: 2006年01月24日
- / カテゴリー: [価値による行動選択 (expected value)] [神経経済学 (neuroeconomics)]
- / Edit(管理者用)
2005年06月22日
■ 行動分析学Q&A
行動分析学Q&Aの [条件性強化子の効力について」スレッドにて理研の松元健二さんと島宗理氏とのやりとりで行動分析学とニューロサイエンスのコラボレーションに関する言及を発見。とくにこの記事など重要。
- / ツイートする
- / 投稿日: 2005年06月22日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
2005年05月10日
■ Nature Reviews Neuroscience 5月号 Sugrue論文続報
"CHOOSING THE GREATER OF TWO GOODS: NEURAL CURRENCIES FOR VALUATION AND DECISION MAKING." Leo P. Sugrue, Greg S. Corrado and William T. Newsome
Nature Reviews Neuroscienceに[Newsome '04 Science 選択行動]スレッドで採りあげたScience論文の続報(というかDorris論文との関連づけのディスカッション)が載っています。 まだちらっとしか見てませんが、以前問題としていたSugrue論文とDorris論文との関連について議論していたところがもろに取りざたされているようです。私としてはLocal time scaleとglobal time scaleとを明確に分けて議論することでSugrue論文とDorris論文の間に一見あるように見える矛盾を解消する、というのは納得のいく感じがあります。
20050117のコメント欄にuchidaさんからコメント書き込みあります(レスポンス遅れてすみません)。最新のエントリでないとコメントが目立たないのでここに採録しておきます。uchidaさんwrote:
ご無沙汰しています。新しい総説、Sugrue et al (Nature Review Neurosci., 2005)、ご覧になられたことと思います。知りたかった解析(Sugrue et al., 2004 のデータをDorris et al, 2004 の方法で解析すること)が出ていますね (Figure 7)!!! 少なくともこれらふたつのニューロンはとても似た振る舞いをしていることが分かります。Population data をきっちりみたいところですが、Newsome グループがこのニューロンを出してきたということは、お互いほぼ同じようなニューロンを見ていると考えるのが自然のような気がします。驚くべき一致ですね!!! 従って、今後はどのように解釈するかということが主眼になるかとおもいますが、そのあたりは今後のGlimcher の反論も含めてじっくりみていく価値がありそうですね。
この総説で強調されている、local な解析・モデルが「メカニズム」により近いはずだから、グローバルな解析より重要だという主張は一理あります。しかし、図7は、expected value が task 中、グローバルに変動しない場合(以前私の書き込みで示したように matching task ではグローバルには expected value が変動しない)、ニューロンの発火頻度も大きく変動しないということをはっきり示しています。Newsome らに決定的に欠けているのは、Dorris et al. (2004) で行われた報酬量を変化させる実験、つまりexpected value をふる実験で、これをしない限り、localな細かな変動をあたかもすべてのように語るのは大きな間違いという気がします。大きな方手落ちです。 Dorris らが示したように、報酬量を変動させたときには local fluctuation よりもずっと大きな変動を起こすことが考えられるからです。そういうことから考えると、この総説の一方的な攻撃に反して、Glimcher らが結局正しいということになるのではないかという予感がします。この総説が、著者の意図に反して大きな欠陥をさらけ出してしまうのではないか。。。
はたからみているだけでなく、自分もなにか面白いことを始めなければ。。。
けっきょくのところ、local valueとgloval valueとがどう関係づけられるか(行動的およびニューロンメカニズム的に)というあたりの解明が進めることがこの戦いに決着を付けるのではないかと思います。SFNでの報告を見る限り、Glimcherたちはbasal gangliaのニューロン記録も進めているようなのですが、そういう意味ではそれは正しい道のように思えます。
- / ツイートする
- / 投稿日: 2005年05月10日
- / カテゴリー: [価値による行動選択 (expected value)] [神経経済学 (neuroeconomics)]
- / Edit(管理者用)
2005年01月17日
■ Dorris and Glimcher (2004)とSugrue et al(2004)(mmrlさんより)
mmrlさんが1/4コメント欄で言及していた計算をしてくださったものが届きました。許可をいただいたので以下に掲載します。mmrlさん、いつもどうもありがとうございます。ここから:
ちょっと計算してみましたのでご報告。
やったことは、matchingとmaximizing(強化学習、Optimization)で得られる解が違うのかどうかをSugrueらの離散時間型のVI-VIスケジュールで確認しました。
結論を先に言うとVI-VIの場合、
- maximizingの解はmatchingの解に一致する
- このときの各expected value for choiceは等しい
の2点です。
maximizationでは違う解が得られるのではないかと期待していたのですが、一致してかつuchidaさんが数行で計算した結果をいろいろいじくって確認しただけとなりました。また、簡単のため選択変更後遅延(change over delay, COD)はこの計算では用いていません。
7月1日に計算したように、n 回あるchoice Aを選択しなければ、そこに報酬が存在する確率は、
と表されます。ここで、は1回に報酬が降ってくる確率。
今、確率的に行動選択するとして、A を選択する確率とすると、まったくランダムに選択したとするとそのinter choice interval の分布
は
このとき、expected value for choice A, はchoice probabiltiy の関数になって、
となります。同様に
これは、を下げれば下げるほど
を上げることになります。
一方、income の方は
となりますからを下げれば0に漸近、1に近づければ
に漸近します。
maximization では、ある選択確率 のときの単位時間当たりの総報酬を最大化するわけですから、
が最大になるように、を見つければよいので微分して0に持っていけばよい。
ここで、となることに注意すると
において から
によって最適解が与えられる。
すなわち均衡解というわけです。
さて、これで得られる解が
fractional income
のどのような関数になっているかというと と
から
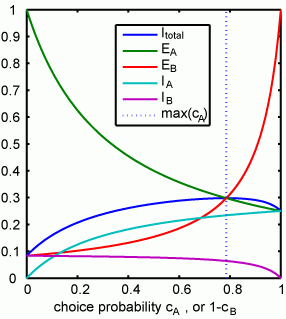
すなわちAのfractional incomeはAのchoice probability に一致する。つまりmatchingというわけです。あーつまんない計算だった。
休み2日掛けて考えたのに結局VIVIはmatching とmaximizingが一致するように巧妙に仕組まれたタスクということだけがわかりました。
これって実はBaum 1981, Heyman 1979, Staddon Motheral 1978に書かれていたいりして...、調べてから計算しよう。ああ、無駄してしまった。
7月1日に書いたことも実はmomentary maximization theory (瞬時最大化理論)と呼ばれるものと同一だったりすることを[メイザーの学習と行動」を読み返して気づいてみたり...。無駄ばっかり。
ここまでです。編集過程で間違いが混入していたらお知らせください。
いやいや、無駄ではないですよ。手を動かした人がいちばん問題を理解した人になると思いますし。
メールにも書きましたが、generalizedでないMatching lawが成り立つためにはchange over delayの導入とVI-VI concurrentであることとが必須であるという理解だったのですが、今回の計算からするとchange over delay自体はalternating choiceのstrategyを排除するためだけに必要で、そんなにエッセンシャルなものではないのかもしれませんね。
しかしここまでくるとchange over delayとtauを組み込んだときにmaximizationとmatchingとの解がどのくらいずれるかということも検証できてしまいそうですね。それについては将来の著者たちの研究を待つか、ガッツのある方の参入を期待するということで、まずはmmrlさん、ありがとうございました。
- / ツイートする
- / 投稿日: 2005年01月17日
- / カテゴリー: [価値による行動選択 (expected value)] [神経経済学 (neuroeconomics)]
- / Edit(管理者用)
# uchida
ご無沙汰しています。新しい総説、Sugrue et al (Nature Review Neurosci., 2005)、ご覧になられたことと思います。知りたかった解析(Sugrue et al., 2004 のデータをDorris et al, 2004 の方法で解析すること)が出ていますね (Figure 7)!!! 少なくともこれらふたつのニューロンはとても似た振る舞いをしていることが分かります。Population data をきっちりみたいところですが、Newsome グループがこのニューロンを出してきたということは、お互いほぼ同じようなニューロンを見ていると考えるのが自然のような気がします。驚くべき一致ですね!!! 従って、今後はどのように解釈するかということが主眼になるかとおもいますが、そのあたりは今後のGlimcher の反論も含めてじっくりみていく価値がありそうですね。
この総説で強調されている、local な解析・モデルが「メカニズム」により近いはずだから、グローバルな解析より重要だという主張は一理あります。しかし、図7は、expected value が task 中、グローバルに変動しない場合(以前私の書き込みで示したように matching task ではグローバルには expected value が変動しない)、ニューロンの発火頻度も大きく変動しないということをはっきり示しています。Newsome らに決定的に欠けているのは、Dorris et al. (2004) で行われた報酬量を変化させる実験、つまりexpected value をふる実験で、これをしない限り、localな細かな変動をあたかもすべてのように語るのは大きな間違いという気がします。大きな方手落ちです。Dorris らが示したように、報酬量を変動させたときには local fluctuation よりもずっと大きな変動を起こすことが考えられるからです。そういうことから考えると、この総説の一方的な攻撃に反して、Glimcher らが結局正しいということになるのではないかという予感がします。この総説が、著者の意図に反して大きな欠陥をさらけ出してしまうのではないか。。。
はたからみているだけでなく、自分もなにか面白いことを始めなければ。。。
2005年01月10日
■ Dorris and Glimcher (2004)とSugrue et al(2004)
どうも遅くなりました。頭がなかなか戻らないのでとりあえず思い出せるかぎりでレスポンスします。
まずはuchidaさん、すばらしいコメントをどうもありがとうございます。こういうサイトをやっていてよかったと思うのはまさにこういうときです。サイトなしにはなかなかお知りあいになる機会のなかった方とお知りあいになることができて、自分ひとりではできなかった議論を日本中、世界中をまたいですることができる、こういうことを積み重ねてネットワークを広げていくことができたらすばらしいと思ってます。
……global な相関(あるいは変動しないこと)と、local な相関、つまり、論文中の3つの仮説のうちのふたつ……の関係をもう少しきっちり詰めることが、この論文で示されたデータを読み解き、Sugrue et al (2004) との関係をはっきりさせる上で重要だと思います。
では、Sugrue et al論文の方はどうかというと、以前(7/5) Sugrue et al論文がglobalなmatchingとlocalなmatchingとを明示的に比較するようになっていない、ということを指摘しました。つまり、Sugrue et al論文ではLIPのactivityでglobal matchingを説明することはできなかったので、時間的にlocalなところのことしか考えていないのです。彼らはglobalにexpected value of choicesが等しいということが成り立つところでの現象を見ていないのかもしれません。
一方で、Dorris and Glimcher論文では基本的にglobalなtime scaleでナッシュ均衡が起こっていると見なしたうえで)、expected value of choicesとresponse probabilityとを分離しようとした試みである、と言えます(localなtime scaleではナッシュ均衡は成り立っていません)。
そうなると両者のあいだで見られるような矛盾はたんに見ようとしているタイムスケールの違いで解決するのかもしれません。この点でryasudaさんのご指摘にあったように、
……Nao(Uchida-san)'s statement (R_A/N_A = R_B/N_B) is not generally true for the leaky-integrator model
matching taskにおいてlocalなtime scaleではR_A/N_A = R_B/N_Bが必ずしも成り立たない、ということは大きな意味を持っていると言えます。つまりryasudaさんの予測にあるように、Sugrue et alとDorris and Glimcherのどちらにおいてもexpected value for choicesが等しいと言えるのはglobalなtime scaleでの話であって、localなtime scaleではどちらの論文でも成り立っていないのです。それで、Sugrue et alはlocalなところに話を終始させたし、Dorris and Glimcherはじゅうぶん均衡に達していないデータを使ってたのでchoice probabilityもexpected valueも変動してしまっている、というわけです。
では、Sugrue et al の model と強化学習のモデルの違いの本質はどこにあるのですか?
そもそもmatching law自体は経験的な法則であって、matching lawがどういう原理によって成立しているのかということ自体が論争になっていることについて以前触れました(6/30など)。いくつかの説の中で、Optimization (= reinforcement learning)をした結果マッチングが起こっている、という説に関しては、メイザー自身がoptimizationよりもマッチングのほうが説明力があるというデータを呈示しているらしいです(6/30)。
また、uchidaさんのご指摘に関連するところでは、Melioration theory(逐次的改良理論)という説をメイザーは押しています。Melioration theoryとは、二つのchoiceのあいだで選択数/強化が等しくなるように選択をした結果、マッチングが成り立つ、というものです(手元に「メイザーの学習と行動」がないのでhttp://www.montana.edu/wwwpy/Faculty/Lynch/MazurChap14.htmを参考に)。まさにこのリンクにも書いてありますが、逆数を取ればpayoff rate (= reinforcement/no of choices = expected value for choices)で、uchidaさんが見出したものと同じものとなります。つまり、Melioration theoryが正しいとすると、二つの選択肢のexpected valueが等しくなるように選択率を調整することによってその結果、マッチングが成り立つ、ということになります。これは二つの選択肢に関してindifferentになるように選択する、というまさにゲーム理論的な行動の現れと取ることができます。じっさい、以前リンクした"高橋雅治(1997) 選択行動の研究における最近の展開:比較意思決定研究にむけて"でも最後のほうに選択理論とプロスペクト理論とを関連付ける(将来的に融合される)という展望について語られています。
というあたりまで見渡してみると、uchidaさんのご指摘はまさにいまホットな話題である部分に直接関わることであり、今後の意思決定の研究がどういう道具立てで行くべきか、つまりゲーム理論/強化学習/選択理論をどう統一的なフレームワークで扱うか、ということに関する本質的な議論なのではないかと思います。
- / ツイートする
- / 投稿日: 2005年01月10日
- / カテゴリー: [価値による行動選択 (expected value)] [神経経済学 (neuroeconomics)]
- / Edit(管理者用)
2005年01月04日
■ Dorris and Glimcher (2004)とSugrue et al(2004)に関して(by uchidaさん)
uchidaさん@Cold Spring Harbor laboratoryからDorris and Glimcher (2004)とSugrue et al (2004)とに関するコメントをいただきました。許可をいただいたので以下に掲載します。今日はuchidaさんによるゲストブログということで、<blockquote>に入れないで地の文に入れます。なお、uchidaさんはリンク先をご覧になればおわかりのようにratのolfactory系によるdecisionの研究で成果を出しておられる方です。
Dorris and Glimcher論文とSugrue et al論文とを比較して、Dorris and Glimcherではchoice probabilityをexpected valueからdissociateできているのではないか、というご指摘です。これはDorris and Glimcher論文のSugrue et al論文に対するneuesを評価するにあたって重要なご指摘であるかと思います。私ももう少し考えてみるつもりですが、皆様のコメントがいただけたらと思います。ここから:
最近見付け、読ませて頂いています。こういうサイトで論文を深く掘り下げることができれば大変ためになりますね。ますますの発展をお祈りしています。以下は大部分すでに議論されていたことの繰り返しになりますが、私なりの意見を述べさせていただきたいと思います。
[Neuroeconomics]
Dorris and Glimcher (2004) および、Sugrue et al (2004) は、Barraclough et al. (2004) と共に、新しい研究パラダイムを切り開きつつあるという点で、大変興味深く見ています。ただ、3論文とも行動の解析は非常におもしろいのですが、実際に神経生理の研究という視点で見た場合、どれだけ新しいパラダイムがいかせているか、という点をもう少し考えてみる必要があるのではないかと思っています。3つの論文を比べると、その点においては、Dorris and Glimcher (2004) がもっともうまく行動パラダイムをデザインしているのではないかという印象を持ちました。
[Local fractional income and choice probability]
Sugrue et al (2004)は、matching behavior が、”local” なreward history (”local fractional income”) で説明できるということを提案したという点が非常におもしろいです。このモデルは、非常にparsimonious で、しかも従来のglobal matching に比べてmechanistic に非常にstraightforward で、その点が優れていると思います。何と言ってもglobal なvariable interval schedule を知らなくても、matching が実現できるというわけですから。
一方、Sugrue et al (2004)の限界のひとつは、”response probability”*1と、”local fractional income” が非常に相関していて切り離せないために、結局、LIP neuron がどちらをコードしているのか(このふたつのどちらかと仮定して)を決定できない点にあるのではないでしょうか。以前、Newsomeのトークを聞いていたとき、この点を質問されて、local fractional income がresponse probability をコントロールしているので。。。deep question だというようなことを言って逃れていました。
[Desirability or expected value of choice]
一方、Dorris and Glimcher (2004)がみているのは、desirability of actionあるいはexpected value of choiceで、後に述べますように、これは fractional income とは少し異なる概念です。すでにこのサイトで議論されているように、subjective vs. objective あるいは、expected utility vs. expected valueの関係、違いは、この論文の議論の弱点であると思います。しかしここでは、その点を差っぴいて、LIP neuron のactivity が結局何と相関しているのかを読む点に力点を置きたいと思います。そのために議論の厳密さが失われることも考えられますが、その点はご容赦ください。Expected value of choice と、local fractional incomeの違いは Daw and Dayan (2004) でも軽く触れられていますが、以下でもう少し考えてみたいと思います。
Dorris and Glimcher (2004)では、Nash equilibrium に達していると仮定するとふたつのchoice のexpected value (本来なら expected utility)が等価になることを利用して、expected value と、response probability を切り離すことを実験のデザインの肝としました。そして、LIP neuron は、inspection game中、response probability が変化しても(Nash equilibrium と仮定して)relative expected value of choice が変化しないときには発火頻度が変化しないが、instructed saccade trials で報酬量を変化させてrelative expected value of choiceを変化させたときにはそれに伴って発火頻度が変動することを示しました。
さて、ふたつの論文は一見似た結論に達しているように見えるかもしれませんが、全く正反対の結論に達していると言ってもいいのではないでしょうか?これは、matching task で、expected value of choice がどうなっているかを考えると明らかになります(式で考えなくても明らかだと思いますが。。。)。
[Expected value in matching task]
サルが、あるブロックでターゲットA, B (red or green)を選んだ回数を、
とします。また、そのブロックで報酬を得た回数をそれぞれ
、
とします。
すると、expected value for choice A および B は、
となります。(expected value for choiceは、一回のchioce あたりに得られる報酬量の期待値で、Daw and Dayan, 2004 で return と呼ばれているものに相当すると思います。)
ところで、このブロックで global matching が起こっていたとすると、、
をAおよびBを選んだ確率 (response probability) とすると、
が成り立つわけですが、
から、
つまり、choice A、choice B に対するexpected value for choiceが等価であることを示しています。つまり、matching task においても、relative expected value for choice がinspection game と同様の振る舞いをしている可能性が考えられます。このことは、おそらくlocal な計算をした場合でも成り立っているのではないかと想像しています。
このことからmatching task では(fig D, in Daw and Dayan, 2004にあるように)variable interval schedule を変化させても、relative expected value for choice (relative return) は変化しないと考えられます(もちろんlocal なfluctuation はあるち思われますが。。。)。従って、Sugrue et al (2004)は、積極的に、「LIP neuron は、relative expected value for choice をコードしているのではない」という結論に達する可能性も考えられます。逆に、Dorris and Glimcher (2004)は、積極的にresponse probability と相関していない点が彼らにとって重要な点です (Fig. 7)。Local fractional income とニューロンの活動が相関していないことは直接は示していませんが。。。
[trial-by-trial variability of desirability of choice]
Dorris and Glimcher (2004) では、その後、LIP neuron の細かな trial-by-trial variability が、”dynamic (local) estimate of relative subjective desirability” と相関しているかを検証しています。どちらの選択をするべきかその時々のdesirability は、opponent を演じていた computerが用いていたreinforcement learning algorithm を使って推定されています。その結果、LIP neuron の発火頻度が relative desirability と相関している、と主張しています(Fig. 9)。
では、この “desirability” とはそもそも何でしょうか? desirability は、少なくともcomputer opponent では、computer の選択をバイアスさせる値ですので、当然、desirability とresponse probability は相関しているはずです。。。従って、上で検討した response probability と LIP neuron の発火頻度を切り離したという議論がどこまで成り立つのか、あるいは、どういう形で成り立つのか、という点に疑問が残ります。そういう眼でもう一度 Fig. 6A を見てみると、確かに、各ブロックごとの平均発火頻度はほぼ変動していないように見えますが、各ブロック内でのlocal な変動に注目してみると若干response probability と相関して変動しているように見えるところもあります。単に想像に過ぎませんが、「response probability から各ブロックでの平均 response probability を差し引いたもの」を考えると、LIP neuron の発火頻度と相関しているのかも知れません(単なる読み過ぎの可能性も大ですが。。。)。
いずれにしても、global な相関(あるいは変動しないこと)と、local な相関、つまり、論文中の3つの仮説のうちのふたつ、”whenever the animals are at a mixed strategy equilibrium during the inspection game, the average firing rates of LIP neurons should be fixed ”と、”On a trial-by-trial basis, however, the mixed strategy equilibrium is presumed to be maintained by small fluctuations in the subjective desirability of each option around this fixed level caused by dynamic interactions with the opponent” の関係をもう少しきっちり詰めることが、この論文で示されたデータを読み解き、Sugrue et al (2004) との関係をはっきりさせる上で重要だと思います。その点が私にはまだはっきりつかみきれていない点でもあります。
もちろん、ひとつの領域にrelative expected value for choiceと、local fractional income をコードするニューロンが混在している可能性も考えられ、ふたつの論文は、その中の両極端のものを見ている可能性も考えられます。お互いの解析を両方のデータを使ってやって比べてみるということが必要ではないかと思います。あるいは、Sugrue et al (2004) のmatching task 中に報酬量を変化させて、local fractional income と相関した変化と、報酬量の変化に伴う相関との度合いを比べてみると、全体像がもう少し分かるのではないかと思います。例えば、Sugrue et al (2004) Fig.4でみられた相関は、Dorris and Glimcher (2004) で見ていた local なfluctuation に対応し、報酬量の変化はもっと大きなLIP neuron の活動変動を引き起こす可能性も考えられます。また、どちらの論文も population data の示し方が不十分なので、そのあたりをきっちりやればもっと何が起こっているかが良く分かったのではないかと少し残念に思います。
uchida
以上です。どうもありがとうございます。編集過程で間違いが混入していたらお知らせください。ひきつづき私もコメントを書く予定です。
- / ツイートする
- / 投稿日: 2005年01月04日
- / カテゴリー: [価値による行動選択 (expected value)] [神経経済学 (neuroeconomics)]
- / Edit(管理者用)
# Gould
ああ、uchida師匠!ついに僕の尊敬する人々がこの日記に集結することに・・・離れた場所にいる、こんな豪華なメンバーで議論がなされているとは、blogの一つの理想型を見ているように思います。ますます見逃せなくなりました。pooneilさん、実のないコメントで申し訳ありません。1年待って下さい。そうしたら、僕もここの議論に少しでもお役に立てるようになります。精進します。
# mmrluchidaさん、ご無沙汰しております。
matcing taskでもInspection game同様にexpected value for choiceが変動しないのではないか、という議論は確かにその通りであり、だとすると、Sugrue et al 2004 とDorris and Glimcher 2004は同じ領域からまったく違う細胞を記録したことになるというご指摘、すばらしい。
以前、計算したようにVI-VIではあるchoiceのresponse probability を下げれば下げるほどexpected value はあがり、response probability を上げればexpected valueが下がる。自然と報酬が得られる確率が自らのresponse probability に連動するような形で入っているから、これはゲームと同じ。ゲームでは、相手が自分のresponse probability をlocalに見て、それを元に相手側の行動(ここではreward probability)を変動させ、それがexpected valueを変化させる。最終的にたどり着く先はequilibrium、すなわちそれぞれのexpected value for choicesが等価になるが、これはGlobal matchingで得られる解と同じという計算には、目からうろこが落ちました。
Dorris and Glicmcher でもlocal にはそのfluctuation が神経細胞活動に反映されているように見えるところもあり、本当のところは互いのデータを互いの方法で解析するか、Sugrue側のタスクで報酬量を変動させたcontrol taskを用意するかしないとわからない。
なるほど、鋭いご指摘です
結局、choice probabilityとexpected value for choices
を分離するには、
1. choice probability 変動, expected value 固定
2. choice probability 固定, expected value 変動
の両方の課題を行って神経細胞がどっちに相関を持つのかを特定すればよい。1はVI-VIやinspection gameでできるとして、2は両者でできているのか?
Platt and Glimcher 1999の課題ではchoiceはさせていないので、これでコントロールを取ったというDorris and Glimcherはダメ。
やはりSugrueのようにVI-VIで量を変動させるのが最も近道でしょうか?
と、uchidaさんの話を繰り返しまとめただけで、私はなんのコメントにもなっていませんね。もうすこし考えよう....
# pooneilGouldさん、まさにit's a small worldですね。
mmrlさん、重複分を削除しておきました。システム変更のためにお手数かけてしまい、恐縮です。
見当違いで袋叩きにあうかと思っていましたが、少し安心しました。よく分からない点は、Dorris の強化学習アルゴリズムと、Sugrue のモデルがどれだけ似ているものかという点です。もしほぼ同じであれば、ふたつの論文は、local な変動という点ではほぼ同じ物を見ていて、Sugrue がglobalにはそれほど変動しないことを見落とした、という結論になる可能性も考えられます。ただ、Sugrueのモデルはglobal matchingをうまく説明できるという点を考えると上の可能性はあまりあたらない気もします。一方、Dorrisの強化学習アルゴリズムがglobalに動くとしたらそもそもdesirabilityと呼ばれているものは何なのかという疑問が出てきます。
Sugrue et al (2004)へのコメントとして、Daw and Dyan (2004) では、"Several questions arise. First, this task has deeper psychological than computational roots. The field of reinforcement learning has focused on a different class of task, which allows for choices to have delayed consequences. "とあります。では、Sugrue et al の model と強化学習のモデルの違いの本質はどこにあるのですか?このあたりは mmrl さんや pooneil さんが詳しそうですね。コメントを頂ければ大変嬉しいです。
なお、mmrl さんの下の段落は、expected value を local income (or local total value) とした方がすっきり行くのではないかと思います。
「以前、計算したようにVI-VIではあるchoiceのresponse probability を下げれば下げるほど local income はあがり、response probability を上げれば local income が下がる。自然と報酬が得られる確率が自らのresponse probability に連動するような形で入っているから、これはゲームと同じ。ゲームでは、相手が自分のresponse probability をlocalに見て、それを元に相手側の行動(ここではreward probability)を変動させ、それがlocal incomeを変化させる。最終的にたどり着く先はequilibrium、すなわちそれぞれのexpected value for choicesが等価になるが、これはGlobal matchingで得られる解と同じという計算には、目からうろこが落ちました。」
ところで、これだけ議論されてもますます面白い、そういう論文が書いてみたいですね。。。
# uchida自分のコメントへの訂正。
「以前、計算したようにVI-VIではあるchoiceのresponse probability を下げれば下げるほど local income は下がり、response probability を上げれば local income が上がる」
これがmmrlさんの意図したものと違っていれば申し訳ありません。
# RyoheiんSorry in English, but I cannot read this diary with my w3m, which I usually use for writing Japanese.
This might be minor point, but Nao(Uchida-san)'s statement (R_A/N_A = R_B/N_B) is not generally true for the leaky-integrator model.
In the model, P_A(t) is given by Int dt' pR_A(t')exp(-t-t')/tau (Int: integral, pR_A: probability to have income from A). In other words, there is a delay in P_A(t) response to a certain change of pR_A. Thus the change of R_A causes a transient change in the expected value for choice A, pR_A(t)/P_A(t), for a period of tau. In this period, the pR_A(t)/P_B(t) should not equal to pR_B(t)/P_B(t) generally. If pR_A(t) changes continuously, the expected value for choice also changes continuously.
I am not sure how does it affect the whole discussion, though .
By the way, a happy new year, folks !
# pooneilryasudaさん、movable typeは書き込みのときにJavaScriptを使っているのでw3mやlynxでは書き込めないんですよね。お手数かけます。w3mで読むときはいかがでしょうか。Lynxではとりあえずメインページは読めるようなのですが過去ログを見るのに不便があるようです。
# Ryoheiん(Further thought from the last comment)
Note that the time course of the expected value for choice (E_X(t):X = A, or B) is a first derivative of pR_X(t) blured by a filter with decay constant of tau. Thus obviously these two values are tightly relate: just a integrator (neuronal?) circuit can translate R to E.
I think the Nash equilibrium would take about the same time as the leaky-integration time (tau). So, probably the stiation may be the same in the other paper too.
Pooneil-san: I know this is my problem sticking to the old-fashioned text browser, but I cannot read Japanese text in this site (MOJIBAKE shimasu).
# RyoheiしIt seems like several typos in my last comment.....
Anyway, I had a brief chat with Nao, and I think both of us agreed that the expected value for choice is time dependent. Interestingly, it is a bit tricky to define the time-dependent expected value, because expected value is statistic value. If a process is not in an equilibrium, ensemble statistics does not equal to time-averaged statistics any more.
I am looking forward to pooneil-san's further comments !!
# mmrluchidaさんのコメントに関して
Daw が言っている`` The field of reinforcement learning has focused on a different class of task,..''の意味についてですが、強化学習では系列をなした一連の行動の後に報酬が与えられ、その系列行動を強化するような学習も含むと言うことだと思います。
このような問題では、choiceした後の直近の報酬のみではなく、将来にわたって得られる報酬の合計を最大化するようにchoiceをしなければならない。本来は、1回の試行におけるdecision が状況を変化させ、次の試行以降における報酬に影響するような(Tanaka SC et al 2004等)のタスクを使わないと、こういった将来の報酬に関する活動は見れません。Sugrue et al にしてもDorris & Glimcherにしても、得られる報酬の量や確率が1回のchoiceのみに依存して決まっている。扱っている問題が強化学習の分野で言うimmidiate reward のタイプの課題を使っていますので、その意味でdifferent class of taskなのだと思います。
では、このimmidiate reward での強化学習モデルとSugrueが使ったモデルの本質的な違いはなにか?
強化学習モデルと言ってもいくつかの学習モデルが考えられ一概には言えないのですが、重要な点は単位時間に得られる総報酬を最大化しようとするのが強化学習モデルであって、Sugrueが使っているのは単なるMatchingの変形版に過ぎないので、必ずしも総報酬が最大になるとは限らない。
でもSugrue et al 2004のnote 19 で言っているように、動物の行動を説明するのにたいした違いはないっていってますね。``we make no clain that our fractional income model captures the ultimate computation going on inside the animal's brain. The model is descriptive not mechanistic --''
なーんて開き直ってますが、おいおい、おめーさん心理学じゃなくて神経科学やってんじゃねーのか!と突っ込みたくなります。
私のコメント「以前、計算したようにVI-VIではあるchoiceのresponse probability を下げれば下げるほどexpected value はあがり、response probability を上げればexpected valueが下がる。」
expected value をDawの言うreturnと同じものだと思えばこのままでよい。各行動をしたときに得られる報酬の確率の意味で書いています。
VI-VIの場合、理論的には選択しないとそこに報酬が存在する確率は増えるって図を7月1日あたりに乗せてもらった思うのですが...pooneilさん、引越しするときに消えてません?
これに対してlocal incomeは単位時間あたりの報酬確率のlocalなものなので、responce probability が下がれば同様に下がりますから、内田さんの言うのもまた正しい。
もうすこし厳密なことがいえるような計算をいまちょっとしてますので、お待ちください。
また、Dorris の強化学習モデルによるゲーム課題とVI-VIでの報酬確率の変動の関係は、定性的には同質であることは直前のコメントで述べましたが、厳密には違うはずで、どこがどのように同じでまた違うかは検討を要します。こちらも時間をください。
# uchidaryasudaさん、mmrlさん素晴らしいコメントありがとうございます。直感的な思考ではなく、実際に数式やsimulationで考えないと良く分からないところも多いですね。
mmlrさん、確かに、VI (Poisson)では、そちらを選択しないうちに、expected value は上がりますね。そういう意味だとは気付いていませんでした。これは、VI-VIの奥の深いところで、Newsomeらも”natural environment” と言っていますが、たとえば、木の実が熟すというようなことを考えれば、一回食べ尽くしても、時間が経つうちにまた訪れてみる価値が上がるという「奥の深い」現象ですね。そういう意味では、ethological な視点からもおもしろい現象です。おそらく、生物が得意とするべく進化してきた、そういう背景もありそうです。
人々がどういう意味で強化学習という言葉を使っているかは勉強したいと思います。
続報も楽しみにしています。私ももう少し詳細を考え直してみます。
# pooneilお返事滞っていて申し訳ありません。mmrlさん、消えた図の件ですけど、直しておきました。6/31というありえない日のエントリだったもんでいじってる過程で消えてしまったようでした。ではまた。
# pooneil私のコメントは新しいエントリに書きました。1/10のところをご覧ください。このエントリも長くなってきたのでコメントは新しいほうに書いていただいたほうが埋もれないかと思いますのでよろしくお願いします。
2004年07月05日
■ Science Newsome論文つづき
もうちょっと核心に向かいましょう。月曜の朝がjournal clubなもんで。
このScience論文にもいろいろな問題はあると思いますが(叩いて埃の出ない論文はない)、私が重要なものと思うのは、(1) この論文がglobalなmatchingとlocalなmatchingとを明示的に比較するようになっていない、(2) matchingよりももっと簡便な説明変数があるのではないか、という点です。なお、以下の文章はこの論文がacceptされるべきかどうかにcriticalな論点と今後証拠が出てくれば十分であるものとが混ざっています。ご注意を。
(1) この論文がglobalなmatchingとlocalなmatchingとを明示的に比較するようになっていない。これはかなり意図的に回避している感じがありますが、そういうわけにはいきません。まず、behaviorですが、Fig.2にあるようにいくつかのmeasureを持ってきてlocal matching lawがよく行動を説明することを示しているわけですが、これはロジックが間違ってます。Globalなmatching lawが当てはまることはよくわかっているのですから、local matching lawはglobal matching lawでは説明できないようなfractuationを説明できていることを示さなければならないのです。ちょっとまどろっこしいですね、つまり、Fig.2でlocal matching lawで説明できている、としているところからgobal matching lawでも説明できる部分を差っ引いてやるべきなのです。それでも説明力があるときはじめて、local matching lawがglobal matching lawに加えて役に立つ説明として採用されるべきなのです。GLM的に考えてやりましょう。Fig.1の選択を従属変数Y(t)、incomeを説明変数X(t)とします。X(t)はgobal matching lawによるregressor X1(t) (Fig.1Cでの黒い直線)とlocal matching lawによるregressor X2(t) (Fig.1Cでの黒い曲線から黒い直線を差し引いたもの)とに分解できます。それでY(t) = a1*X1(t) + a2*X2(t) + a3*X1(t)*X2(t) というふうにモデルを組んでやることができます。これでcoefficient a1は有意なのはわかっているので、coefficient a2が本当に有意なのは検証してやればよいのです。Fig.1Cなんてチャンピオンデータなんですから、全てがこうだと信用するわけにはいきません。交互作用の項があるのは、global incomeが1:1と1:8とではlocal incomeの違いの選択への影響が変わりうるからです。長くなりました。なんにしろ、彼らはこういうことはやっていません。つまり、読者は彼らの言うlocal incomeというやつにはglobal incomeの影響が足し合わさっていることを忘れてはなりません。じつのところ、global matchingだけが成り立ち、localなfractuationはそのmatchingからの予測のエラーを最小化するような強化学習のパラダイムで考えた方が尤もらしいと思うのです。だからこそ、global matchingかlocal matchingか、という問題はnontrivialなはずなのです。
また、電気生理学的にも、local incomeのことだけ考えているという点には難点があるのは上記の通りですが、要するに話はとしては、LIPのactivityでglobal matchingを説明することはできなかったということです。だからlocalな方へ話を持っていこう持っていこうという流れにFig.2がなっているのです。これはつまり、(a) 非験者はglobal matchingなどしていない、local matchingだけ、(b) 行動としてはglobal matchingもしているんだけれどLIPはそれには関与していない、のどちらかであるのでしょうけれど、この問題を彼らは回避したのです。それはもちろん、(a)のようなことは言うのは行動分析学者の反感を引き起こすでしょうし、(b)のようなことを言うのはせっかくmatchingのことをやろうとしているのに狙うべき領野を間違えた、ということになるのですから。というわけでどっちでも彼らにとって都合が悪いのです。そして我々はそれを責めるべきです。つまり、ここでもglobalなmatchingとlocalなmatchingとの問題を回避した影響が出ているのです。実のところ彼らはglobal matchingなんていらないという立場でやっているのですが(local matchingさえあればglobal matchingはいらない、もしくはglobal matchingはlocal matchingの結果をglobalに眺めたものに過ぎない)。
また、すでにmmmmさんが6/22のコメント欄で指摘していますが、電気生理でtauを決め打ちしている点には問題があります。個々のまたはpopulationのニューロンのtauと行動のtauとが必ずしも一致している必要はないのですから。じっさい、この問題は以前にMTでのperceptual decision研究のときにも繰り返された問題でして、いろんな感度を持っているニューロンがあって、それらをどう統合して行動に結び付けているのか、という話になるのです。
(2) matchingよりももっと簡便な説明変数があるのではないか。絶対に検討しなければならないことは、今回の「matchingに関連したvalueのneural correlate」という言い方以外のもっとより簡便(parisimonious)な説明はないか、ということです。たとえば、attentionだけで説明できないか、ただのmatchingとは独立なdecisionの確信度みたいなものでは説明できないでしょうか。Control taskとmatching taskとでの違いとは、両者を比べるmatchingをしているかいないか、というよりはFig.4では二つのターゲットからのselectionをしているが、Fig.3のcontrol taskではselectionをしていない、という違いではないでしょうか。とくに、control taskではlocal incomeの違いはサッケードするターゲットを選択するのに役に立ちませんが、Fig.4のmatching taskではlocal incomeの違いがサッケードするターゲットを選択するのにcriticalな情報となっています。つまり私はこの論文で見つかったことの本質は、LIPニューロンはただ単にlocal incomeの比率のような量をコードしているのではなくて、これがdecision makingに関わるときにのみdecision variableとしてその情報がLIPで処理されている、このことだけではないかと考えるのです。そう考えてみるとやっぱりPlatt and Glimcherとの違いがいったいどの程度あるのか、という問題になります。また、Jeff SchallがFEFでさかんに研究したような複数のターゲットからのselection、というパラダイムと結び付けて考える価値があるような気がしてきました。
(2)についてまた違った言い方にしてみましょう。Matching lawは二つの間での選択だけではなくて、ある一つの行動をするかしないかという選択にも応用できます。ということは、Fig.3にあるようなコントロールタスクでもそういうmatching lawが効いているということになります。また、このコントロールタスクはターゲットが一つしかないVI強化スケジュールをやっていることになります。つまり、Fig.4のマッチングタスクとFig.3のコントロールタスクとの間でのcriticalな違いとは、どっちのターゲットを選ぶかのdecisionが要るか要らないか、という点です。この点において、Fig.3とFig.4との違いからPlatt and Glimcher論文とNewsome論文との比較をすると、decisionをするときにreward関連の情報があるとそれを加味したようなrepresentationをLIPがするという意味では両者は同じです。Fig.3のような結果に関してもPlatt and Glimcher論文でも同様なコントロール実験を持ってくればよいだけで、わざわざmatching lawを満たすような実験にする必要性はここまでではありません。よって、もうひとつ「Fig.4のマッチングタスクとFig.3のコントロールタスクとの間でのcriticalな違い」を持ってくる必要がありますが、それは上記の選択をしているか否かを選択行動理論的にパラフレーズすれば、並列強化スケジュールであるか単一強化スケジュールであるか、二つの選択でのmatching lawと行動するかしないかのmatching lawとの違い、ということになるでしょう。
- / ツイートする
- / 投稿日: 2004年07月05日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
2004年07月04日
■ Science Newsome論文つづき
 、ついでに"Glimcher Review")。まあ、この間のVernon SmithとDaniel Kahnemanのノーベル経済学賞で心理学と経済学の組み合わせが脚光を浴びたから次は神経科学と経済学というわけですな。しかしこりゃあもう陣地は取られているような感じですな。なんかもっと違うことを考えなくては。
追記:mmmmさん、ありがとうございます。コメントではリンクできないようです。こちらでリンクしておきます。
そういう意味ではラットでたくさんありそうですね。
、ついでに"Glimcher Review")。まあ、この間のVernon SmithとDaniel Kahnemanのノーベル経済学賞で心理学と経済学の組み合わせが脚光を浴びたから次は神経科学と経済学というわけですな。しかしこりゃあもう陣地は取られているような感じですな。なんかもっと違うことを考えなくては。
追記:mmmmさん、ありがとうございます。コメントではリンクできないようです。こちらでリンクしておきます。
そういう意味ではラットでたくさんありそうですね。
- / ツイートする
- / 投稿日: 2004年07月04日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
# mmmm
このあたりの関連としては例えばCardinal et al. (2001): Impulsive choice induced in rats by lesions of the nucleus accumbens core (http://www.sciencemag.org/cgi/content/full/292/5526/2499)でしょうかね。
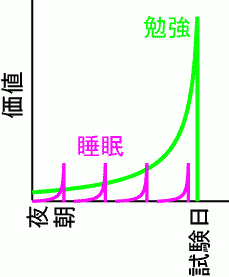
# mmrl彼らのlocal matchingは、過去の報酬履歴に対する効果が薄れて行くという話しであって、それに対して、上に書いてある図は未来の報酬に対する予測がdiscountされる方の話をしていてちょっと違うのではないでしょうか?さらに、「メイザーの」ではexponential discounting をしてましたか?わたしの理解だとhyperbolic discountingではないかと考えます。というのも、exponential curve を使うと睡眠が勉強を追い抜くことはないと思うのですがどうでしょう?上の図を作るとき実はhyperboric curveを使ったりしてませんか?(もしくは、discount rate を勉強と睡眠で違うものを用いていませんか?)
# pooneilありがとうございます。あんまりよくわかってないかもしれませんが、私の絵自身はexponentialで書いてます。勉強と睡眠とでdiscount rateは変えてありますが、それはその方がリアリスティックだと考えたからです。なんにしろ、今回の論文とはあんまり関係ないというのはその通りでして、なんか身につまされて面白かったので図にしてみた、というのが正直なところです。
# mmrlなるほど、違う種類の報酬には違うdiscount rateを用いるほうがリアリティがあるかな。どうも強化学習理論にとりつかれていると、最大化する報酬は同じ基準で比較するのがよろしいと頭からおもってしまっていけませんね。人間でもいろんなdiscount rateで価値を計算、比較してるってのは本当なのかもしれません。
# mmmmこの陣地争いに対等に加わっているのは、日本では銅谷さんのところが挙げられるでしょうか。Nature NeuroscienceのAOPに出た論文が、マスメディアで盛んに取り上げられていますね。この分野のサル屋さんはちょっと不甲斐ないというか、時代から取り残されているかも(落胆)。その次の時代を牽引すべくお互い頑張りましょうねー。
# pooneil”Prediction of immediate and future rewards differentially recruits cortico-basal ganglia loops”、これですね。玉川のCOEシンポジウムでもしゃべってましたね。プログラムに書いたメモに[GP SNr: stochastic action selection] -< [striatum: action value (expected reward / candidate action)] なんて書かれてます。なんにしろ、経済学でなくてもいいんだけれど、なんらかの形で役に立つような形を見出せるようにアンテナを張っておきたいと思います。これは基礎科学をする人間にとって忘れるべきでない点ですし。
# pooneil追記:銅谷さんの論文の解説がhttp://www.jst.go.jp/pr/info/info87/index.htmlにあります。
2004年07月01日
■ Science Newsome論文つづき
"Matching Behavior and the Representation of Value in the Parietal Cortex." Leo P. Sugrue, Greg S. Corrado, William T. Newsome
mmrlさんから6/29のコメントにあるbayesian harvestingに関する詳しい解説と図が届きました。どうもありがとうございます。以下に掲載します。今日はmmrlさんによるゲストブログみたいなもんですので、<blockquote>に入れないで地の文に入れます。貼り付けてある図は図2の方です。図1は6/30のところに貼ってあります。はてなは一日一枚しか画像が貼れないもんで。なぜか図が小さくなってしまったので6/29にもっと大きい図2を貼っておきました。そちらをご参照ください。 (追記:はてなからの移行の際に図の配置を直しました。図1、図2ともに下に貼りました。)
mmrlです
先日説明したbayesian harvestingですが、図をはさんでいただけるということですので、ちょっと計算をしてみました。Corrado のポスターの式を参考にしました。すでにpooneilさんがやさしい言葉で説明されているVI-VIの場合に最適行動はmatching にほぼ等しくなることを式で書いただけというだけです。少々長くなりますが、私のような式や実際に動くプログラムやロボットで納得する人間のエゴとお許しください。
離散時間で進行するVI-VI平行スケジュールはある確率で報酬が出現し、取るまでそのままという形で実現できます。毎回red/greenに報酬が出現する確率をp_red/p_green とすると、greenに報酬が存在する確率P(r_green)は前回greenをためした回からの回数をkとしてP(r_green)_k = 1-(1-p_green)^k となります.
なぜなら,
1回では
p_green,
2回では最初の1回で出現する確率+1回目で出現せず2回目で出現する確率=
p_green + p_green(1-p_green),
3回目では
p_green + p_green(1-p_green) + p_green(1-p_green)^2
となり
k回目では
p_green (1 + (1-p_green) + (1-p_green)^2 + ... + (1-p_green)^(k-1))
となり等比級数公式から
P(r_green)_k = p_green(1-(1-p_green)^k)/(1-(1-p_green)) = 1-(1-p_green)^k
red を選び続ければ、p_greenがどんなに小さくてもP(r_green)_kは1に漸近しますから、
ほぼ100%でgreenに報酬があることになります。
ここで、baysian harvestingとは、報酬の存在確率を初回をP(r_red) = 0 , P(r_green) = 0 として上の式にしたがって計算し、その回(t)におけるP(r_red)(t) > P(r_green)(t)ならredを逆ならgreenを選ぶ最適選択者とします。とすると図1にあるようにredが上回ればredを選択し、確率0にリセット、green が上回れば..という周期パターンで行動を選択することになります。
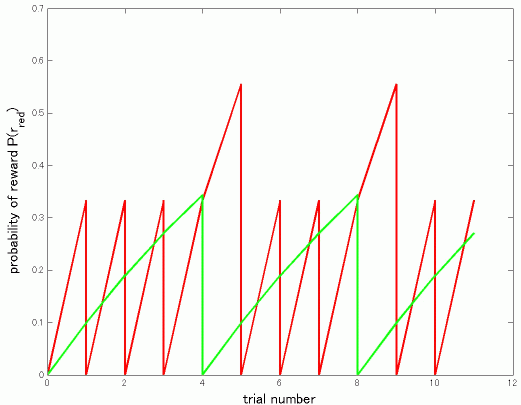
figure 1
ここで、p_red > p_green の場合に限定して考えると、redを選ぶ回数n_red(>=1)回に1回green を選ぶパターンになるはずです。(図1では3回に1回p_red = 1/3, p_green = 1/10)
したがって選択の割合はn_red:1となり、このときn_redは log(1-p_red)/log(1-p_green) の小数点きりすて整数になります。
なぜなら,n_red回はredを選ぶので報酬存在確率は
p_red > 1-(1-p_green)^n_red
次の回でこの関係が逆転するので、
p_red < 1-(1-p_green)^(n_red+1)
これを変形して (1-p_green)^(n_red+1) < (1-p_red)
の両辺をlog取って変形すると
n_red > log(1-p_red)/log(1-p_green) -1
となる最小整数がn_redであるから、
n_red = floor[log(1-p_red)/log(1-p_green) ]
ここでfloor[x]はx以下の最大整数
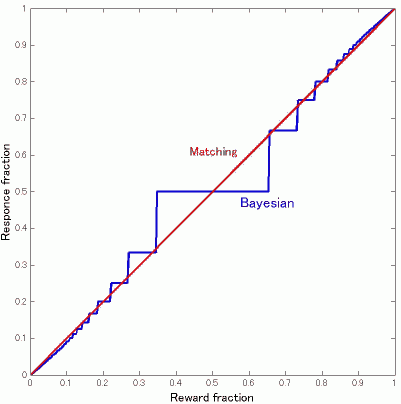
figure 2
これで得られるn_redを使って選択割合、n_red/(1+n_red)を報酬割合p_red/(p_green + p_red)の関数としてプロットすると図2のようになります。(p_red + p_green = 1/3の制約を与えています)。matching は、選択割合と報酬割合が一致するのですから傾き1の直線になります。ごらんのような階段関数となりますが、n_redが増えるにしたがって接近しているのがお分かりいただけるかと思います。ただこれが完全に一致するかというとどうかわからないところです。細かいところまでみると、どうも完全に一致しないように思います。
mmrlさん、どうもありがとうございました。すごい。
ひとつコメントですが、図2ってスムージングをかけてやると、逆S字型のカーブになりますが、それってgeneralized matching lawでいうところの過小な適応(強化の比率ほどには選択の比率が0.5からズレない)の形に近似できる感じがします(スムージングをしてから両座標をlogスケールにすると傾きが<1になる)。Bayesian harvestingによってやや過小ぎみな適応をしている、ということになるとじつはこっちの方がFig.1にある青線と黒線のずれをよく説明できるような気もしてきます。(あ、過小じゃなくて過大だったかも。)
そういえばVI-VI並列強化スケジュールとVR-VR並列強化スケジュールに関しては"高橋雅治(1997) 選択行動の研究における最近の展開:比較意思決定研究にむけて"に記載がありました。VI-VR並列ではVIのほうがより多く選択されることや遅延低減仮説に関して書かれています。やっぱりこのへんまだいろいろありそうです。
- / ツイートする
- / 投稿日: 2004年07月01日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
# mmrl
すみません、いきなり間違い発見しました。1つめの囲み記事の最終行は「ほぼ100%でgreenを選択するようになります。」です
# mmrlもとい「ほぼ100%でgreenに報酬があることになります。」
# pooneilありがとうございます。直しておきました。
# mmmmmmrlさん、大変分かりやすい図とご説明、ありがごうございました。非常によく解りました。さて、mmrlさんの図との対応を考えるにあたって、実際に何トライアルくらいに1回、報酬を貰っていたかが気になってきました。議論を単純化するため、overall maximum reward rate (0.15 rwd/sec)を採用しましょう。また常にtargetが表示され続けていたと仮定して考えると、1トライアルに要する時間は平均1950ms + rewarding timeとなるでしょうから、大体2秒と考えてよさそうに思います。0.15 rwd/sec = 1 rwd/6.66 secですから、平均3−4トライアルに1回の報酬があったと考えられます。これはgreenとredの両方を加算した条件ですから、p_red:p_green = 1:1の場合を考えると、red choiceに報酬が与えられたのはそのうちの半分ですから、6−8(平均約7(本当は6.6))トライアルに1回ということになり、red choiceによるreward rate、p(r_red)は単純計算で1/7 = 0.14となります。ここでmmrlさんの図2を見てみると、MatchingとBayesianとの間の一致はかなりよいレベルです。以下同様にp_red:p_green = 3:1の場合p(r_red) = 3/14 = 0.21p_red:p_green = 6:1の場合p(r_red) = 6/24.5 = 0.24p_red:p_green = 8:1の場合p(r_red) = 8/31.5 = 0.25となります(あくまで概算)。p(r_red) = 0.25でもMatchingとBayesianとの間の一致はかなりよいです。ということは必ずしもMatchingである必要はなくて、Bayesianでも説明可能なのではないかということになりそうに思えます。つまり、そろそろ別のターゲットに報酬がつきそうだということをベイズ的な計算に基づいて予想して、選択するターゲットを切り替えているのではないか、というように思えます。このことは、reward rateの小さい方のターゲットを選択する間隔がどれだけ周期的になっているか、また、その選択の切り替えが、mmrlさんの図1で予想されるタイミングにどれだけ一致しているかを検討することで見えてくるのではないでしょうか。ただ、pooneilさんの調査によると、CODを用いているとのことなので、この影響をどう考慮するかも考えなければなりませんね。
# pooneil直しておきました。
# mmmmん?↑の私のコメントでは、p_red + p_green = 1の制約が度外視されているような……。
# mmrlたしかに、bayesian でもよい予測はでき、行動が周期的かどうかを議論することで違いは出せると思いますが、bayesian は細かい短期記憶を必要とする(Matchingに比べて)複雑なモデルなので、オッカムのかみそりを使うと簡単なモデルで説明つくならそっちでいいじゃないかということになる。もし周期性が本当に観察されるなら、bayesianが本当っぽいということになるのかもしれませんが、それはでそうにないのではないかと考えます。なぜなら、bayesian では完全に行動ごとの報酬出現確率を既知として計算されている。本来は確率はサルにはわからないわけで、これを学習する必要があるはずです。しかも報酬出現確率は突然変化するために、常に学習しようとすることが報酬の最大化につながるはずです。とすると各試行におけるサルの行動は完全にはbayesianで予測できるとはおもえない。やるならば、長い時間スケールでは報酬出現確率を学習し、短い時間スケールでは報酬存在確率を考慮しながら行動をするのが最適になるのではないかと考えています。じつはこれはSugrue et al のsupporting online material のfigure S1 choice trigger averaging (CTA) of rewardと関係があって、彼らはこれはうまくexponential curveで近似できているといっていますが、私はこの曲線は異常に3-5trial 前までが大きくなってうまくフィットしない様に感じるのです。これは上に説明したような2重のタイムスケールを持つ学習/決定モデルでフィットできないかと考えています。モデルに関してはまた後日考えて見たいと思います。それと私のミスで、図2の制約条件はp_red + p_green = 1/3です。ごめんなさい。pooneilさん何度も申し訳ないです。overall maximum reward rate (0.15 rwd/sec)で1試行で約2secですから、報酬率は約0.3ということで、大体あっているはずと思って1/3にしました。たしかSugrueのポスターにも約1/3という記述があったように記憶しています。
# mmrlpooneilさんコメントありがとうございますスムージングを掛けてlogとってみるとどうなるか?って話ですが、実は図2の階段関数は、実はめんどくさくて数値解しか出していないので、解析解をみてみないと厳密にはなんともいえないです。ただこのカーブはp_red + p_greenの値に依存して変化します。1/3のときはよくあっているように見えますが、1にするとS字カーブになることを確認しています。
# mmmmああ、そうか。単純に1/3を1:1, 3:1, 6:1, 8:1に分けるだけでよくて、実際の実験状況でのp(r_red)はminimumが1/3 * 1/2 = 0.167、maximumが1/3 * 8/9 = 0.296となると見るだけで良かったのか。先のはダサダサしたね(笑)。
# mmmm報酬出現確率が本当にサルにとって未知であるかどうかは検討する必要があるのではないでしょうか。長期のトレーニングによってサルは、トータルの報酬出現頻度が約1/3であり、しかも報酬のred/green (or green/red)の比率が、1/1, 3/1, 6/1, 8/1しかないことをサルはすでに学習済みである可能性があると思います。するとブロック毎に学習すべきは、どの比率であるかの選択だけでよいことになります。そして各ブロックは100-200 trialsを含んでいますから、そのほとんどを既知の確率に基づいて行動していることはありそうなことではないでしょうか。
もしかしたら、mmrlさんの考えと基本的には同一なのかもしれません。モデルの方も期待しています。
なるほどそうか、長い訓練でいくつかの確率のパターンをいくつかあらかじめ知っていてそれを選択するということも考えられますね。考えていませんでした。わたしが考えていたのは単純にbayesianで予測される報酬の確率と実際の報酬との誤差が確率をupdateさせるモデルです。mmmmさんの言われる方法でも別にモデルができますね。ただ、いくつかのモデルを当てはめることができても、これをどうやって比較したらいいんだろう...。自分でVI-VIの行動データを取ろうかな? もう少しつめる必要がありそうです。
# mmrlbayesian harvesting にchange over delay を入れてみた場合も、一応計算してみました。結果はあんまりかわらなくてがっくししたのですが、まず、CODのもっとも簡単な形はswitchした後は1回は報酬をあげない、だけどもう一回選んだらあげることにします。Sugrue 04のReference and Notesの11に書いてあることをそのまま理解するとこれをしていることになります。ならば簡単switchしたらもう一回は必ず同じ色を選ぶことにする。問題は、これをするとswitchしたほうがよいかstayしたほうが良いかは2試行先まで見て平均報酬の良いほうを選ぶことです。以前と同様にp_red > p_green の場合に限定して話を進めます。redにいるとき、2試行まで見越してやるとp_red < {1-(1-p_green)^n_red+2}/2の関係が成り立つ最小整数n_redを求めればn_redを連続で選択する回数がわかります。結果はn_red = Max{floor[ (1-2p_red)/(1-p_green) ] -1 , 2}となります。同様にn_greenももとめて、p_red/(p_red + p_green)に対してn_red/(n_red+n_green)を求めれば同じようなグラフが得られます。結果はほとんど同じ、ステップは細かくなりましたが、概要は同じでした.これを使ってモデルは作ってやってみましたが、どうもstay dulation(Fig 2 F)がサルの結果にあわないようです。CODの関係でどうしても2回が多くなる。やはりここまで複雑なことは考えていないかも知れません。
# pooneilp_red + p_green = 1/3、直しておきました。
# mmmmmmrlさん、お疲れさまでした&ありがとうございました。Fig. 2Fでは2回が多いですから、モデルの方がそうならなかったという意味ですね?行動の解析には報酬の各比率のトライアルがが必ずしも均等に含まれているとは限らないので、比率毎に分けて、彼らの行動の結果を見てみたいところです。そのデータがあれば、もう少し妥当なモデル化ができるようになるのではないかと思いますが、これは彼らのみぞ知るデータで、続報(がもしあれば)に出てくるのかもしれないので期待したいところです。
2004年06月30日
■ 速報

mmrlさんから6/29のコメントにあるbayesian harvestingに関する詳しい解説と図が届きました。どうもありがとうございます。今日の欄はもういっぱいなので、明日のところに貼らせていただきます。追記:図は7/1の図1です。はてなは一日一枚しか貼れないんですよ。
- / ツイートする
- / 投稿日: 2004年06月30日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
■ Science Newsome論文つづき
"Matching Behavior and the Representation of Value in the Parietal Cortex." Leo P. Sugrue, Greg S. Corrado, William T. Newsome
また、行動をいかにmatching lawに対応するように統制するかという点では"change over delay" (COD)を導入している点が重要であるようです。これはどういうことかというと、選択を続けていく過程でそれまで赤を選びつづけていたときから緑を選ぶようにスイッチしたとき(逆に緑から赤へのスイッチでも)にちょうど報酬を与えるタイミングであったときには報酬を与えるのを一試行分遅らせて、もう一回スイッチした色を選択してから報酬を与える、とするものです。つまり、あんまり頻繁に赤と緑どっちを選択するかを変えることにはコストがかかります。CODを導入することによって左右を交互に選ぶ"alternating strategy"(ずっと交互に赤と緑を選ぶ)や"win-stay-lose-switch strategy"(報酬が得られたら同じ色を選ぶけれど報酬が得られなかったら違う色の方にスイッチする)を断念させようとするわけです。このCOD戦略はオリジナル論文であるHerrnstein '61でも採用されているようです。
というわけで結局のところ、並列VIとCODを使うことでmatching lawに対応するように行動を統制しているということのようです。
このあいだ私はmatching lawが必ずしも最適解ではない例を挙げましたが、あれはVR-VR並列強化スケジュールでの例でした。VI-VI並列強化スケジュールではmatching lawはほぼ最適解と一致します。直感的にわかるように書きますと、強化率の比率が右:左で1:10だったとします。この場合左だけ100%選ぶのは最適解ではありません。VRではないので試行数が多ければよいわけではないのですから。右もたまーに選んでやればいいのです。CODがあるなら二回連続で。なぜならずっと右を放置しておいてから右を選べば一発で(CODがあるのなら二発で)ほぼ確実に報酬が得られるのですから。これだけで左を100%選びつづけるよりもより多く報酬が得られます。
これとは別に、「メイザーの学習と行動」にはmatching lawと最適化理論との間の関係および論争についての記載があります。つまり、その都度最適解を選ぼうとすることによって結果的にmatching lawを満たすような関係が生まれるのではないかといったような。そこでメイザー本人がScience '82論文でmatching lawと最適化理論との間でのpredictionが乖離するような実験パラダイムを組んで検証したところ、matchingのほうのpredictionの方が当たっていた、ということが記されています(実験パラダイムは複雑そうなのでスキップしときました)。しかし上記のようにVR-VR並列強化スケジュールの例とVI-VI並列強化スケジュールの例とを見てみると最適化理論の方がそれらしいようにも思えてきます。以前挙げたSeoungの"matching and optimization are two ends of ..."によるとこの二つはどのくらいの時間的スパンのヒストリーを選択のときに考慮するかの違いということで統合できるらしいのです。つまり長いスパンでは最適化、短いスパンではmatchingというように。読んでないけど。
と、それからまだNewsome論文の実験条件ををちゃんと書いていなかったのでここで書いておきましょう。Subjectはfixation pointを固視します。赤と緑のtargetが同時に左右のそれぞれどちらかに現れます。どちらかにサッケードするのですが、与えられる報酬は並列VI強化スケジュールになっています。"overall maximum reward rate is set at 0.15 reward per second"と書いているのがなにげによくわからん。MaxでVI6.6secなわけだけど、ではincome ratio 1:1のときが赤緑ともにVI6.6secで、1:8なら片方がVI6.6secでもう片方がVI52.8secで、ということだろうか。ちょっと今のところ自信ありません。ところでfixation breakしたらどうなるんだろ。Incomeのhistoryなんてかんたんにぶっ壊れそうな気がするのだけれど。
- / ツイートする
- / 投稿日: 2004年06月30日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
# mmmm
なるほど、随分スケジュールの全貌が明らかになってきました。”change over delay”というんですか。うちの学生さんから聞いたことのある手法ですが、正式な用語があるとは知りませんでした。「メイザーの学習と行動」未読で、図書館にも所蔵がなかった(涙)ので発注しました。”overall maximum reward rate”ですが、赤も緑もコミコミでってことじゃないでしょうか。
# pooneilありがとうございます。maximum reward rate = 0.15 reward/secと捉えれば(VIなので実際には必ずしも報酬が用意された直後にタスクをしているわけではない、という意味でのmaximumというのが正しそう)、overallはmmmmさんのご指摘の通り、redとgreenあわせたものと考えるほうが妥当なようです。Red:greenのincome比が1:2なら、redで0.05reward/sec、greenで0.10reward/sec、というように。
2004年06月29日
■ Science Newsome論文つづき
"Matching Behavior and the Representation of Value in the Parietal Cortex." Leo P. Sugrue, Greg S. Corrado, William T. Newsome
強化スケジュールについてまとめましょう。これは強化(=報酬)がタスクの回数または経過時間とによってどう決まっているかを示すものです。タスクの回数の場合がR(ratio)、経過時間の場合がI(interval)で確率的揺らぎを加えてあるのがV(variable)、与えられていないのがF(fixed)で、FR,VR,FI,VIとなります。
まず、FR(fixed ratio)は一回のオペラント反応(私の分野ではほとんどタスクの一試行)に対して与えられる強化(私の分野ではほとんど報酬)が固定されているものです。我々のタスクではたいがい一試行で一回報酬が与えられていますからこれはFR1と表示されます。彦坂先生の1DR taskは四方向の試行ひとかたまりで一回だけ報酬が与えられることからFR4と書けます(報酬が与えられる試行は四試行ごとにあるわけではないので正確にはFR4ではないのでしょうが)。(追記:これは間違い。強化されるターゲットはある一方向で、その方向は毎回報酬が与えられるため、その方向だけFR1であって、他の方向は強化されない、と考える方が正しいようです。また、四方向の刺激はブロックになっており、報酬の出る方向だけに反応すればよいわけではないので、四方向のターゲットは独立ではありません。よって独立した並行強化スケジュールというわけではありません。)
つぎにVR(variable ratio)は試行と報酬との関連が確率的になっているものです。たとえば平均二試行に一回報酬が与えられるけれど三試行で一回の場合もあれば一試行で一回の場合もあるものをVR2と書きます。つまり松元健二さんと田中啓治先生のScience '03では1/2の確率でしか報酬が与えられないことからVR2と言えるでしょう。(追記:同じくこちらも間違い。またこちらも報酬ありの刺激にだけ反応すればよいわけではないので、reward+刺激とreward-刺激の強化スケジュールは独立ではありませんので、普通の並行強化スケジュールとは違っています。)
FI(fixed interval)は試行の回数によらずに経過時間によって報酬が与えられるものです。たとえばFI10secでは10秒のintervalで報酬が与えられますが、実際にもらえるのは10秒経った後に試行をした直後です。そして報酬が与えられるとまたその10秒後以降に試行をすれば報酬が与えられます。つまり、一番楽をする方法は10秒ごとに一回だけ試行をして毎回報酬を得るというものですが、実際にはそんなに正確に時間を計測することもできないので、そろそろ十秒かなというあたりで何回か試行をして報酬を得ることになります。このため、時間あたりの試行の回数はVRなどと比べてずっと低くなります。さっさと試行数を稼ぎたいならFRかVRです。
VI(variable interval)は上のFIでintervalに確率的ばらつきを与えたものです。たとえばVI10secなら平均10secでまた報酬がもらえるようになりますが、あるときはそれが2秒で、あるときはそれが20秒かもしれません。このため、VIはFIと違って報酬を得た直後に試行の速度がダレません(なぜならばまたすぐに報酬がもらえるかもしれないから)。このため、安定した試行のペースを保てるとともに(FIと比べてのadvantage)、報酬が与えられなくなったときの消去もすばやく行われます(FRやVRと比べてのadvantage)。
このVIを二つ使って平行して二つの刺激を強化する(緑のtargetと赤のtargetそれぞれを独立に強化する)、という並列強化スケジュールVI-VIで選択をさせる、というのがmatching lawが一番うまく当てはまる条件であるらしくて、matching lawの実験では一番よくこれが使われています。というわけでmmmmさんの指摘の通り、今回のNewsome論文では並列のVI強化スケジュールが使われています。
以上を踏まえてmatching lawについてもっと正確に定義してやると、強化率の比率が選択の比率に一致する、ということなのです。つまり、Herrnstein '61のハトをsubjectとしたオリジナル論文にあるように、片方のキーがVI3minでもう片方のキーがVI1minのときに(強化の比率が1:3)キーへの反応の比率が1:3になる、というのがオリジナルのmatching lawです。Newsome論文でのincomeという使い方にどのくらいの普遍性があるかはよくわかりません。
また続きます。
- / ツイートする
- / 投稿日: 2004年06月29日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
# mmmm
Matsumoto et al. 2003で用いられたスケジュールは、VR2ではなくて、FR1-FR0 concurrent scheduleではないかと考えます。それはともかく、VI-VI concurrent scheduleでmatching lawが一番よくあてはまり、それ以外の強化スケジュールではそれほどではないのだとしたら、それが一体何故なのか、やっぱり気になります。そろそろ別のターゲットで報酬が貰えるというタイミングの予測に基づいた行動に特徴的だったりしないでしょうか?愚問かもしれませんが、FR-FRの場合だったらどうなんでしょう?ああ、PsychINFOが使えたら・・・。
# mmmmFR0 => FR∞???
# pooneilありがとうございます。そうか、go刺激とnogo刺激は別物だから片方を毎回強化して(FR1)、もう片方はまったく強化されない(FR∞)、と考えるのが妥当ですね。こうやって書いてみると明白だ。ためしに書いてみて理解が深まりました。くわしくは明日書きますが、もうひとつ”change over delay”(別のターゲットを交互に選ぶようなストラテジーをdiscurrageするような方策)も重要なようで、オリジナルのHerrnsteinの’61論文でも使われているそうです。ここらを見ておくと本当にsubjectはmatchingしているのか、という疑問も出ます。また、Matchingが最適化理論などによる帰結なのか、それとも実際の行動の法則なのかという議論も「メイザーの学習と行動」にありました。VR-VRではおそらく過剰な適応(overmatching: 強化率の高い方ばかり選ぶ)が起こるはずです。そのようなばらつきに対処するためgeneralized matching law(過剰な適応、過小な適応、片方の反応へのバイアスを取り込んでmodifyしたmatching law)というのができた、ということと理解しております。うちもPsychINFOないんですよ。こういうとき総合大学はいいなと思います。以前は文学部に行ってBBSコピったり経済学部にってbootstrap法の本コピったりとかメリットを生かせていたのですが…
# pooneilそうやって考えてみると彦坂先生の1DR taskも四方向の一方向だけが毎回強化されて(FR1)、他の方向はまったく強化されない、というふうに考えるべきですね。本文に追記しておきます。
# mmrlあれ、また書き損じ、すみませんpooneilさん、すばらしい解説大変参考になります。mmmmさんご指摘の件について、たしかにVI-VIのときには、一回出た報酬は取るまでそのままですから、そろそろ逆側に報酬がありそうということを考慮している可能性はあるとおもいます。彼ら(Newsomeのグループ)もこのあたりは気づいていて、昨年のneuroscience meeting で、Sugrue氏の横でポスターを出していたCorrado氏このあたりを議論していました。もし取らなければ逆側に報酬が存在する確率が上がるような記憶を持たせ、報酬の存在確率が大きいほうを選択するような最適bayesian harvesting をさせた場合とmatching law との関係を議論していました。結果はreward fraction が0.5付近ではほぼ一定となる階段関数になるのですが, 0.6以上0.4以下ではその階段関数は細かくなり、1や0に漸近してmatching に近くなります(この掲示版絵が載せれるともう少しわかりやすくなるのですが...).答えになっているかどうかわからないですけどどうでしょう。 じゃあ、他の場合はどうなるんだろう?FR1-FR0とかの例はmatsumoto etal 2003や、1DRの場合と比較すればよいのでしょうけど、FR-FRだけでなくVR-VRをやった場合の研究ってないのでしょうか?ってmmmmさんと同じ締めになってしまいました。他人任せにせず自分でもう少し調べてみます。
# pooneilどうもありがとうございます。VR-VRはたぶん昔の論文を見ればあるんだと思います。教科書を読むと、並列VI-VI以外のいろんな条件でmatching lawが満たされることがわかっている、みたいな事が書いてありますから。ただ、それがclassical matching lawなのかgeneralized matching lawなのかで話はずいぶん違ってきますが。あと図に関してですが、もしよければメールで私のところまで画像ファイルを送ってくだされば本文の方に載せますのでお気軽にどうぞ。長辺が300pixelまでの制限があってそれ以上の大きさのものは自動的に縮小されるようになってます。
# mmmmmmrlさん、貴重な情報ありがとうございます。まだ理解不十分ですので、図を期待しています。論文に書かれていることを超えた情報がこれだけ集まってくると、このサイトの意義が見えてきますね。更なる発展を期待しております。
# pooneilmmmmさん、その通りですね>>このサイトの意義。こういう論文を交えた話は事実関係のところであれこれやったほうが面白いわけで、いかに深く、核心までたどり着くか、という方向へ行きたいと思っております。また同時に、このことは各方面の研究の将来性と限界とを検討することになるわけで、今後の脳研究がどういう方向へ行ったらいいかを議論するための重要な材料にもなるであろうことを期待しております。ほんと、ここまで行けたらよいと思ってます。
2004年06月28日
■ Newsome Science論文つづき
"Matching Behavior and the Representation of Value in the Parietal Cortex." Leo P. Sugrue, Greg S. Corrado, William T. Newsome
「メイザーの学習と行動」および「学習の心理」サイエンス社を借りてきました。Matchingなのかoptimizationなのかという問題はすでにメイザーのScience論文でmatchingの方が優位ということで決着がついているらしい*1、VIではmaching法則による解はoptimizationによる解とほぼ同じ、時間的にlocalなところをみるというアイデアはすでにある、などのことをすでに見つけております。
*1:ところでMazurがメイザーだとは私気付いてませんでした。ずっと。
- / ツイートする
- / 投稿日: 2004年06月28日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
2004年06月24日
■ Science 6/18 つづき。
"Matching Behavior and the Representation of Value in the Parietal Cortex." Leo P. Sugrue, Greg S. Corrado, William T. Newsome
今のところこの論文に関してはまだ私は周りから攻めているところですが、論文の内容自体に関しては6/22のところにmmmmさんのすばらしいコメントがあります(こういうのを期待してこの日記やってるんです、私)。ということでそちらの方もご覧ください。mmmmさん、私からのコメントはもう少々お待ちください。
で、周りから攻めてる:Matching lawに関する行動分析学関連でのいくつかの記述をメモ。「選択行動」というのがキーワードのようです。もう少し続きます。
- "『行動分析学研究』掲載論文抄録 Vol. 11 特集:選択行動研究の現在" 目次と要旨
- "坂上貴之(1994)第1章 選択をめぐる実験的行動分析" 要約
- "行動経済学と実験経済学"-"選択行動の研究における最近の展開:比較意思決定研究にむけて" 要約
- じぶん更新日記 2001年9/4
- じぶん更新日記 2001年9/5
- Action Potentials: Diary (2003年02月)
- Mazur: "Learning and Behavior"の14章の解説
- "The generalized matching law describes choice on concurrent variable-interval schedules of wheel-running reinforcement."
- "Probability Matching and the Law: A New Behavioral Challenge to Law and Economics."
- lecture note 非常にわかりやすい。
- "Barker's Chapter 9: Choice Behavior"
- "Study 9: The Matching Law and Concurrent Schedules of Reinforcement."
- スタンダードな教科書 Sutton and Barto "Reinforcement Learning: An Introduction."がのオンラインバージョンで読める。すごい。日本語訳も出てます。
- 強化学習チュートリアル。むちゃくちゃわかりやすい。感動的。
- "強化学習と大脳基底核" 銅谷先生の仕事のまとめ。
- / ツイートする
- / 投稿日: 2004年06月24日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
2004年06月22日
■ Science 6/18 つづき。
"Matching Behavior and the Representation of Value in the Parietal Cortex." Leo P. Sugrue, Greg S. Corrado, William T. Newsome
でもって、まず"the matching law"というものについて説明しましょう(言わずもがなですが、以下の説明は素人である私がまとめたものです。正確なことを知りたい方は「選択行動」でググったり、「メイザーの学習と行動」あたりを読んでみてください)。人間を含む生物がなにかを選択するとき、その選択肢の「価値」に基づいて選択をします。この選択がどういうルールで決まるか明らかにしたのがHernsteinの"the matching law"です。これは、ある二択があったときに(三択でもかまわないけど)、その片方Aを選ぶ比率はそれまでのAを選択したことによるincomeの比率と等しくなる、というものです。
例を挙げてみましょう。
状況:舌切り雀なお、この選択の比率はあくまで何度も選択を繰り返したときのものであって、今度来るかけがえのないたった一回の選択のどっちが当たりであるかを決めてくれません。お婆さんがそうであったように。確率が人生の選択に及ぼす全てのことと同じで。
二択:大きいつづらと小さいつづら
income: 大きいつづらに今まで入っていた米10合 小さいつづらに2合
選択:大きいつづらの方を10/12の比率で選ぶ
状況:バスケットボールどのくらいまでの過去のincomeを考慮するか、ということも重要な変数です。今までの全ての試合の結果を蓄積して考えているか、それともここ最近の試合の結果だけで決めているか(急に3点シュートがスランプになったとしたら、ここ最近のスランプ時の3点シュートのincomeだけで行動を選択する方が賢明でしょう)、というわけです。
二択:3点シュートと2点シュート
income: 今までの3点シュート*10=30点 今までの2点シュート*50=100点
選択:3点シュートの方を30/130の比率で選ぶ
なお、本当にバスケットボールで3点シュートと2点シュートとのどっちを選ぶかを研究した論文があります。"an application of the matching law to evaluate the allocation of two- and three-point shots by college basketball players."
"The matching law"についてはこんな感じで。
んで、Newsomeはこれを左右のどちらかのターゲットにサッケードする、というタスクにしました。右にサッケードしたときにジュースが出る確率が60%、左にサッケードしたときにジュースが出る確率が20%だとしたら(incomeの比率が3:1ということ)、実際に右にサッケードする比率は右対左で3:1になることでしょう。実際にそうなりました。しかもincomeの比率を変えてやると選択もそれによって変化しました(たとえば、incomeの比率を1:6に変えてやると選択の比率も1:6に変わったのです)。
そしてsingle-unit recordingからLIPのニューロンはどちらを選択したかという情報をコードしているだけではなくて、どっちの方がincomeが大きいかという情報(つまりこれが「価値」ということですな)をもコードしているということがわかったというのです。
さて、ではこれがどのくらい新しいか。とくにPlatt and Glimcherと比べて。これを明らかにするためにはPeter Dayanが書いたように、このmaching lawとreinforcement learningとゲーム理論とでどれがLIPニューロンの動態を一番うまく説明できているか、という検証が必要になるでしょう。このへんについてはまた明日以降書きましょう。
なお、DayanもDawもreinforcement learningを研究している人ですので、そこに重点が行くのはよくわかります。(Neuron '04 "Temporal Difference Models and Reward-Related Learning in the Human Brain."およびScience '04 "Dissociable Roles of Ventral and Dorsal Striatum in Instrumental Conditioning."、そしてNathaniel Dawのthesis "Reinforcement learning models of the dopamine system andtheir behavioral implications.")
また、maching lawは必ずしも最適解ではありません。たとえば、incomeの比率が1:8(右:左)だったら、選択の比率を1:8にする(1/9*1/9+8/9*8/9=65/81)よりは、100%左だけ選びつづけた方(8/9*1=8/9)が得なわけです。ですので最適解を求めるようなアルゴリズムとの関係も問題になることでしょう(参考文献:"Matching and maximizing are two ends of a spectrum of policy search algorithms.")。これはたぶんreinforcement learningとmaching lawとの関係自体の問題となることでしょう。このへんについてもまた明日以降書きましょう。
- / ツイートする
- / 投稿日: 2004年06月22日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
# mmmm
まだ途中までしか読んでいませんが、matching lowを分かりやすく解説してくれてありがとうございます。確かこの仕事ではVI (variable interbal) scheduleを採用していたと思うんですが(要確認)、この効果が最適解を採らない戦略を可能にしていると思われます。つまり、そろそろ別のターゲットを選んだ方が報酬を貰える確率が高いはずだということをサルが予想している可能性があります。サルの行動制御をうまく工夫したところだと思いますが、この可能性をどう著者らが考慮しているかは検討に値するように思います。
いや、もしかしたらmatching lawが最適解と一致するデザインになっているかもしれない。
コメントどうもありがとうございます。”Variable interval schedule”がキーワードですか。そのへん調べてみます。どうもありがとうございます。mmmmさんのおっしゃるように、一日のセッションの中で左右のincomeが逆転するところがあることが必須なのでしょう。もし一日中ずっと一定のincomeの比率をキープしたとしたら選択は最適解を選ぶか、という問題でしょうね。これはかなり基本的な事項のようなので、探せば関連する記述を見つけられそうです。
また、Fig.1Cの星印にあるように、実際にはかなりlocalな変動によって選択のbiasが引きずられる(Fig.2Cにあるように最近10trial分ぐらいしかincomeとして考慮していない)、ということからしても、あんまりblock単位でのincomeのbiasを確信もって把握している感じではなさそうです。だからincomeの比率が左右で1:6のblock中にたまたま左でジュースがもらえることが連荘で続いたら、左への選択biasが一時的に上がる、ということが起こっているのでしょう。mmmmさんが言ってることと本質的には同じことですが。
お久しぶりです。ゲーム理論と聞いて、ムムッと感じたのですが、話は至ってオーソドックスそう(って当たり前か)。本文読んでいないのですが、前後関係の要素はどう処理、解析してるのでしょうかね。
# pooneilどうもご無沙汰しております。ゲーム理論、と書いたのは私の早とちりでして、matching lawはどちらかというと行動分析学の分野のものであるようです。ゲーム理論的なアプローチは昨日挙げたNature Nueorscience ’04のほうでした。Nash equilibriumなんて言葉が出たりしてます。あと、今回の論文はオーソドックスすぎて、Platt and Glimcherがやったこととほとんど等価なようにも思えます。つまり、Platt and Glimcherが見つけたreward probilityやらtarget probabilityをコードするLIPニューロンがNewsomeのやったようなincome (= reward probility * target probability)をコードしているのはほとんどあたりまえのようにも思えるわけです。あとはどっちがニューロンの活動のbetter predictorであるかという問題だ、というDayanの言い方に私は賛成です。それから、「前後関係の要素」っていうのはよくわからなかったんですが、incomeの比率を変えたブロック間の順序効果のことでしょうか?
# mmmm今朝、駆け足で通読しましたが、強化スケジュールについての正確な記述(VI, FI, VR, or FR?)は見つけられませんでした。昨年だったか、理研でやったNewsomeのトークでは確かVIだと言ってたんですが。)
この論文の肝は、コントロールタスクではLocal incomeの影響がまったく現れないけれども、matching taskでははっきり現れる、ということのように思います。matching lawとの対応付けに焦点を持ってきたために、この重要な点が薄れてしまった印象を受けます。Matching lawと行動とLIP activityとの対応をきちんとつけるためには、タウの値を変えてneuronal activityを見ると、local fraction incomeとの相関が落ちる、つまり行動でも神経細胞活動でも、最適なタウは一致する、ということを言う必要があるように思います。ただ、ブロックによって、日によって、タウが変わる可能性が高いだろうから、これもできれば押さえたいところ。まあ、これに関連したことがdiscussionで簡単に触れられてはいますが。
なるほど、すばらしいコメント、ありがとうございます。こういう書き込みがあるので日記やっててよかったと思います。大感謝。んでもって、レイノルズのオペラント心理学入門をざっと見てみましたが、今回の論文のはたしかにVIに対応するもののように思えました。いまだポイントがよくわかってはいないのですが、もう少し勉強してみます。
それから、コントロールタスクとマッチングタスクとでのincomeのLIP activityへの影響の違い(Fig.3C vs. Fig,4B)、なるほど納得しました。Platt and Glimcherとの違いもこのへんから議論できそうですね。というわけでもう少しそのへん読んでからコメントします。もうしばらくお待ちください。
あ、もちろん、「私が返事するまで書きこむな」という意味ではありません。何かありましたらまたどうぞ。
横から失礼,まちがえてかきこんでしまいました、scheduleに関してはVIでよさそうです。昨年のneuroscience meetingでのポスターでも本人がそういっていたのを記憶しています。また、すでに気づいているかもしれませんが、:”Matching and maximizing are two ends of a spectrum of policy search algorithms.”が自分のlectureをrmで公開していて、その中でも「最近査読したのだが」とことわってこの論文について説明しています。一見してみてはいかがでしょう?
# pooneilmmrlさん、ありがとうございます。すごい助かりました。H. S. Seungですね。rmってのがわからなかったのですが、http://hebb.mit.edu/courses/9.29/2004/lectures/index.html ここから探したどこか、ということでしょうか? 是非知りたいので教えてください。しかしここにはHerrnsteinの論文とかが載ってて劇的に助かります。
# mmrlええ、それですね、その中のlecture 6の中でLeoの論文について触れています。学部生向けの講義かもしれませんが、かなりやさしいところからふれてくれていて、問題のHerrensteinの論文も解説してくれてます。lecture 7と8の前半あたりでは、参考文献にあげられていたSeung自身の学習モデルの話を解説しています。そのあとは、どうやらゲーム理論の話をはじめていましたが、その後まで到達していません。Leeさんの話も出てくるのかな?それから、rmというのは realvideoというリンクをクリックするとreal playerで視聴できるということです。しかしこの人査読したからって、未発表論文の解説をwebで公開するってのはよいんだろうか...
# pooneilmmrlさん、ありがとうございます。realvideoのことですね。失念しておりました(昔インストールしたreal playerは消してしまった)。聴いてみます。Newsome論文のacknowledgementにH. S. Seungって入っているんですよね。ということはあらかじめSeungに読ませておいてからrefereeとして廻ったということだろうか。それならうまくやった、という感じかもしれない。もう一人のrefereeは神経生理学者として、三人目に本当のmatching lawの専門家(HerrnsteinとかMazurとか)がrefereeに入ってたかどうか重要そうです。
この論文に関するコメントを再開しました(6/29)。あと2、3日続く予定です。
2004年06月21日
■ Science 6/18
"Matching Behavior and the Representation of Value in the Parietal Cortex." William T. Newsome @ Stanford University School of Medicine。 ("Matchmaking."にPeter Dayanによる解説あり。)
6/17に「Newsome苦戦しているな」と書いた矢先でいきなり登場です。
Decision makingをmaching theoryを使って説明して、さらにそれのneural correlateを見つけた、という論文です。関連すると思われる論文に
- Nature Nueorscience '04 "Prefrontal cortex and decision making in a mixed-strategy game." Daeyeol Lee
- Nature '99 "Neural correlates of decision variables in parietal cortex." Platt and Glimcher
今回のNewsome論文もなかなか手ごわそうですが、journal clubで採り上げようかと思うので、これ読んでみることにします。
まず、Peter Dayanによる解説を読むと、なにげにボロボロです。
今日はここまで。
- / ツイートする
- / 投稿日: 2004年06月21日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
お勧めエントリ
- 細胞外電極はなにを見ているか(1) 20080727 (2) リニューアル版 20081107
- 総説 長期記憶の脳内メカニズム 20100909
- 駒場講義2013 「意識の科学的研究 - 盲視を起点に」20130626
- 駒場講義2012レジメ 意識と注意の脳内メカニズム(1) 注意 20121010 (2) 意識 20121011
- 視覚、注意、言語で3*2の背側、腹側経路説 20140119
- 脳科学辞典の項目書いた 「盲視」 20130407
- 脳科学辞典の項目書いた 「気づき」 20130228
- 脳科学辞典の項目書いた 「サリエンシー」 20121224
- 脳科学辞典の項目書いた 「マイクロサッケード」 20121227
- 盲視でおこる「なにかあるかんじ」 20110126
- DKL色空間についてまとめ 20090113
- 科学基礎論学会 秋の研究例会 ワークショップ「意識の神経科学と神経現象学」レジメ 20131102
- ギャラガー&ザハヴィ『現象学的な心』合評会レジメ 20130628
- Marrのrepresentationとprocessをベイトソン流に解釈する (1) 20100317 (2) 20100317
- 半側空間無視と同名半盲とは区別できるか?(1) 20080220 (2) 半側空間無視の原因部位は? 20080221
- MarrのVisionの最初と最後だけを読む 20071213