pooneilの脳科学論文コメント

■ 「統計学を哲学する」(大塚淳著)を読んだ

(注記: 以下はツイートをまとめただけなので断片的。)

「統計学を哲学する」(大塚淳著)を2章の最後まで駆け足で読み進めた。すげー面白い！内在主義的な基礎付け主義の話、JaynesのMaxEntとも繋がりそう。Gelman Shalizi 2013およびそのコメンタリも読みたい。ともあれまずは明日中に最後まで読み切っておきたい。

統計的推定における自然種(Natural kind)としての統計モデル(正規分布とか二項分布とか)を科学における目的に応じた世界の分節化によって説明とか、確率モデル(=大数の法則とiidから措定される「真の分布」)の実在と、道具としての統計モデルの関係(対象実在論)とかも、やっと納得いった。

クワインの認識論的全体論の話も出てきたけど、なるほど、この話が「現象学的明証論と統計学」(田口、西郷、大塚)における、真の分布-推定パラメーター-観測値が互いに依存しあっている構造と繋がるのだなとか。私の頭のシナプスがガンガン繋ぎ変えられてる感じ。

確率モデルの「実在」も、ヒュームまで戻ったら統計的推測できないでしょっていうプラグマティックな視点だったので納得いった。戸田山本では、科学者が無自覚に前提としている素朴実在論を擁護する、みたいな形而上学的な実在と(私には)読めたので、納得できなかった。(<-読み終えてないのに語りすぎ)

---

「統計学を哲学する」(大塚淳著)、最後まで読み終えた。すごくいい本だった。それぞれの章で統計について最小限の数式での説明をした上でその哲学的含意を語り、を繰り返して、最終章でもういちど哲学的含意の部分をつないで説明し直す、ここまでやってトータル229ページでコンパクトにおさめてる。

自分的には最終章もっと深くやってほしいとか、頻度主義が外在主義的認識論でベイズが内在主義的って単純化し過ぎだよなとか思ったが、このあたりは最後の最後(p.228-229)でフォローがあった。

あと、4章のAIC部分についてはすごく期待していたのだけど、ずいぶんあっさりとしたという印象。あまり既存の研究が引かれてなかったので、統計学の哲学としても著作の数がそもそも2,3章と比べて少ないのだろうと思った。ここの部分については「科学と証拠」(ソーバー)を読み直してみようと思った。

5章の因果推論の部分はすごく充実していて、因果とは因果グラフではなくて、実在世界と可能世界との間をつなぐ介入のレベルにある、とかスゲー満足した(<-言い方！) 因果推論については著者の「哲学者のためのベイジアンネットワーク入門」とかでもお世話になった。

というわけで、またこの本をゆっくり読み直したり、「科学と証拠」「科学とモデル―シミュレーションの哲学」「科学的実在論を擁護する」とか途中で積んであるものに戻る手がかりにしたりとかしていく予定。

あと、この本で書かれていた認識論的、意味論的な問題というのは、いま私がやろうとしている、自由エネルギー原理をエナクティヴィズム的に見直すプロジェクトを、その外側から批判し鍛えるのにも使えそう。FEPにおける反実仮想って、Pearl的な反実仮想になってないよね、って話をしたことがあるけど(Granger因果性的な因果しかない)、やはりここは肝だなと思った。

■ Exploratory and confirmatory data analysisの問題

2012/9/25-26

Exploratory and confirmatory data analysisの問題について。p-valueを使うような統計というのは本当はconfirmatory statisticsだから、予備実験でeffect sizeを推定した上で、実験計画をして、effect sizeから検出力を決めた上でnを決めてやる。だけど実験科学者がやっているのはexploratoryの段階で止まっている。だから、べつの研究者による追試が実質上のconfirmatory data analysisの役割を果たしている。だから、以前話題になった“Too good to be true”みたいなことが起こる。

心理物理なり動物心理なりではべつの研究者によって追試が行われるけれども、認知的な課題を使った神経生理学だと追試は事実上無理だったりするので、同じラボから同じ課題で整合性のあるデータが継続して出てくることをもって結果の正当性を保証するというなんとか社会的なやり方になっている。

「データとってから何を検定するか（有意差出るまで）探索する」これはなあ。記録できたデータのパラメータの間でのcovariance matrixみたいなの作ると、どっかで有意なのが出てくるっていう形の誤謬がある。(多重比較の一種だろうけど、こういうのをなんと呼べばよいのだろう。)

行動データ取ると、いろんなパラメーターで評価できる。たとえば眼球運動を記録すれば、応答潜時、end pointのばらつき、trajectory curvature、peak velocity、といろいろ評価できる。だからそのどれかで有意差が付いたとしても記述的な論文でしかなくて、それらを整合的に説明できるような「お話」を必要とする。これは「お話としての説明」と「物理学的な説明」の話に繋がるのだろうと思う。

.@shima__shima ひとつの論文の中であればそれは可能で、充分にeffect sizeが大きいものはbon ferroniくらい厳しくても帰無仮説は棄却されると思います。それよりももっと見えにくいのは、20グループが同じ実験をして、1グループで帰無仮説が棄却されるケース。

因果ベイズネットとか読んでるときに妄想したけど、複数の実験の問題を解決するために、すべての実験の結果を取り込んだ因果モデルみたいなのを作って、実験1ではネットのこの部分を見てて、実験2ではネットのこの部分を見てる。実験結果合わせて、因果モデル全体を評価するとかどうよ、とか思った。

統計の勉強をはじめてかぶれてた頃に、以前属していたslice実験の世界では、n=5で有意差付ける実験をたっくさんやって論理の連鎖をつなげていて、あれはいかんとか言ったものだが、実のところあの世界はeffect sizeがでかいので、統計なんかおまけで、グラフ見れば充分なのだった。

.@syunta525 多重比較って言葉で典型的に指すのは因子が三つ以上あって、薬A,B,Cのあいだの違いみたいなものでしょう。「時系列のデータの各時間ポイントで多重比較する時」こういうのはrepeated measureなのでMANOVAとかで扱うのが正しいのではないでしょうか

時間的相関があるものは自由度の補正が必要なので、それよりかはモデルベースで、なんらかの時間変化のモデルを作ってやって(logistic functionとか、exp(-at)みたいのかと)、その推定パラメータを処置群とコントロール群で比較すべき、というのを読んだことがあります。

それがいちばん正しいと思う。それに従って、昔LTPの実験をしたときには、時系列データひとまとめにしたarea-under-the-curveを一つの実験から計算して、それを処置群とコントロール群で比較するということをやった。

それはマスターのときの仕事の論文だったけど、周りでは各時点ごとにt検定やっている論文ばかりで、どうしょうもないと思ってた。でもそれはいまにして思えば勘違いで、前述したとおり、effect sizeが大きければ統計なんて飾りに過ぎない。そしてそういうところで勝負すべき。

たとえば、10Hzで発火したニューロンが12Hzになりました、とかそういうところで勝負すべきではなくて、まず、100Hzで発火するニューロンを見つけてきて、そいつが50Hzになることを示すべき。

でもそういうはっきりとした話が出来るところはそれなりにもう済んでいる。

以前書いた「神経生理の方と話していて、基本はt検ですよ、と主張するのを聞いてて、気持ちは分かる、たしかにそういう美しい実験デザインを汲んでみたいものだと思うけど」 この話と繋げて再考すれば、強烈な応答さえあればt検で充分なんだ。

今日の話は、以前話題になった「科学と証拠 統計の哲学 入門」 エリオット・ソーバー 著と繋がるだろうか。

「強烈な応答さえあればt検で充分なんだ。」これは根っからの神経生理学者はみんなそう思ってると思う。だから、神経生理学者はあまり統計とかこだわらない。それはむだなところに労力を使わない、正しい行動選択だったんだろう。

.@kohske じっさい、Hubel and Wiesel 1959にt検なんて出てこないですからね。もっと後の時代での、resultがANOVAの値の羅列になるのってのは心理学論文の流儀を移植したものなんでしょう。

神経生理学論文および近接分野ででいつから統計が使われるようになったかを調べて、それぞれの分野の論証の性質と対応づけて議論すれば、SFNのhistory of neuroscienceのコーナーでポスター出すくらいの仕事にはなると思う。一週間で出来る。前例があるかどうかは知らない。

■ サンプルサイズと検出力

ふと思い立って、検出力のカーブを描いてみた。

シンプルに正規分布で、mu=0, sd=1でalpha=5%で検定するとH0:mu=0が棄却される確率は0.05 (横軸0の点)。

さらにH1: mu≠0として、mu=-3:3, sd=1でデータを振ってやって、H0が棄却される確率(1-beta)を横軸にmuをふってplotしてやると、図のようになる。randnでデータ作って、ttestする。べつべつのデータごとにttestに使うデータの数を変えている。

そうすると、データ数5のときは、効果量=abs(mu)>1.6とかでないと1-beta > 0.80にならない。データ数が10,000あると、効果量>0.02とかで1-beta > 0.80になる。要は、effect size小さくてもnさえ稼げればなんでも有意になる。

だから、nがサッカードの数だったりしてデータ数が1万とかあって、応答潜時への効果とか見るとなんでも有意になってしまう。実験データでなくてシミュレーションで有意差付けたりしたことがあるが、これもいくらでもデータが生成できるからいくらでもp値を小さくできる。

サンプルサイズの議論は、効果量がこれこれで、サンプルサイズがこれだけしかないのに有意差出ちゃったときは1-beta計算してみれば<0.8になってるからそれは偶然(もしくは有意になったところでデータ集め打ち切った)だからもっとデータ集めないとだけですよ、みたいな議論は出来るけど、サンプルサイズが異様にでかいときになんか言ってくれるわけではない。

もちろん、効果量をちゃんと書くべきということにはなるが、効果量が小さければ意味がないというものでもない。MRのBOLD変化やEMGのspike-triggered averagingはデータはノイジー(=正規化すると効果量は小さい)だが、それは間接的な計測であることの帰結。

だから統計的有意味性と生物的な有意味性を分けて考えようみたいな話になるわけだけど、「生物的な有意味性」というのはけっきょく社会的合意の産物っぽい。

たとえばポズナー課題でSRTが5ms短くなったとしてそれにどのくらい意味があるかは、なんかべつのものに置き換えて評価するべきなのかも。たとえばspeed-accuracy trade-offを考慮して、5ms応答潜時が早くなることは正答率が何%向上するのと同等であるとか。

ここまで書いて見直してみたが、検出力の意味を説明するには絶望的に説明が足りてないな。まあそういうのは必要に応じて作ることにする。

そういう話ではなくって、データありすぎっていう状況に対していったい何が出来るのだろうかとか考えたかったのだけど、なんだかワケわからなくなってしまった。

効果量と検出力とサンプルデータ数の間には一定の関係があるのだから、たとえば、データ多すぎるときは、推定される効果量とあらかじめ決めた検出力(0.8とか)で必要とされるサンプル数が決まるから、多すぎるデータから適切なサンプル数をリサンプルして、検定を繰り返すとか? p値の確率密度分布、みたいなわけの分からないことになってきた。

もともとH0:mu=0ってのが一点しかないのが間違いで、幅があれば、alphaとbetaのどちらを重視するかっていうpayoff matrixを書いて、それが最適になるようにalphaとbetaを意志決定すればよいのだけど、そうなってない。

alpha=0.05, 1-beta=0.80に固定すると、effect sizeとnumber of sampled dataの関係が決まる。これをプロットするとこうなる。

よく分からないけど、log-logプロットで直線になった。

今回やった検出力のシミュレーションのコードをbitbucketに上げてみた。Subversionからgitへの移行の練習を兼ねて。

■ 信号検出理論の感度(d-prime)にエラーバーを付けたい！(解決編)

以前 「SDTのd'にエラーバーつけたい。」ってのを書いたことがあるけど、このときの図の軸をpではなくてnorminv(p)にしてしまえばd'が等しいところが並ぶのでCDFの計算が簡単になる。

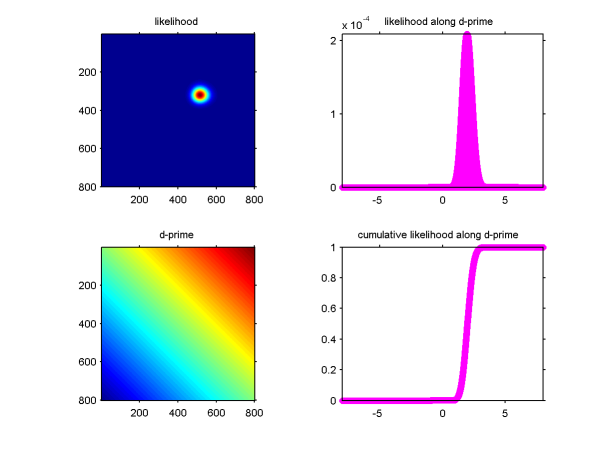
これでconfidence intervalも計算できるんで、解決って思ってたんだけど、元のp(hit), p(fa)での軸も悪くないんではないかということに思い当たった。というのも、大して大きいデータではないので、N=hit+miss, M=fa+crを固定した上で、p(hit), p(fa)をそれぞれ0-1までふって尤度を計算してやれば、たかだかM*N個の尤度の計算で済む上に、もっとも重要なことは、p=0,1での尤度の計算も出来る。

norminvだとここはInf, -Infに発散してしまうのでd'が計算できないわけだけど、それはそれとしてそのデータ点の尤度が計算できるならば、たとえd'がInf, -Infになってしまっても、尤度関数の期待値から、ベイズ推定的にd'の推定値と信頼区間を計算できる。つまり、hit rateが 30/30だったとしても、d'が推定できる。これはよいんではないだろうか。

考え方としては、二項分布で20/20のときの信頼区間計算する話と同じ。

いや、d'そのものは推定できないけど、そのupperboundかloweboundが計算できる。たぶん、hit = 30/30のときに便宜的に29/30だったらd'いくつになるか計算するのと同じことを、もうちょっとまともにやったことになるのではないだろうか。

ここまで考えると、もうちょい逸脱して、d'自体の絶対値にこだわらずに、M*N個の可能なd'のランクに変換して、ノンパラメトリックd'みたいなものを定義してしまえばよい。 探せばこういうのありそうだ。

最尤法で尤度がmaxのところを推定値とするのはMAP推定と等価だけど、maxではなくて分布の重み付け平均を推定値として取るのはなんと呼べばよいのだろう。「ベイズ推定」と呼ぶのはへんな気はするが、noninformative priorでのベイズ推定と言えばウソはついていないのか。

ためしに計算してみた。p(hit) = 30/30で、p(FA) = 10/20の場合。

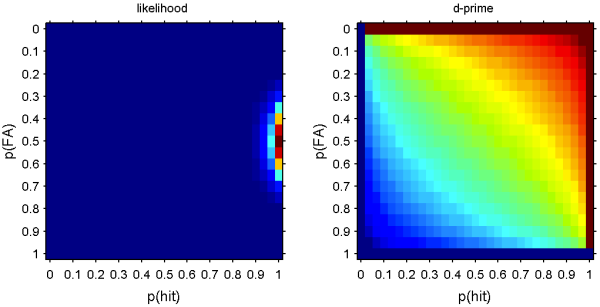
でもって、ここまできたらたぶん、dprime = norminv(p(hit)) -norminv(p(fa)) の式を使うのがアホなんだろうな。ノンパラにするのも極端な話で、二項分布かなんかを持ってきて、ノイズのシグナルの二つの分布の離れ具合はKL距離で評価とかそんなかんじか。

---

超分かった！d-primeのドメインではなくて、[p(hit), p(fa)] 自体のベイズ推定を行えばいいんだ。p(hit)=1だったとしても、30/30と3000/3000とでは推定されるpは違うし、それはけっして1ではない。それを使ってd-primeを計算してやればよい。しかもこれはけっこう実用的だ。

matlab関数作ってみた。たとえば[hit miss fa cr] = [10 0 5 5]の場合、p(hit)=1からはd'=Infになってしまうが、尤度からのp(hit)の推定値は0.95となる。これから計算したd'は1.69となる。妥当なかんじ。

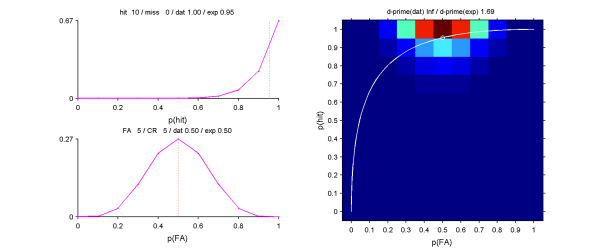
[hit miss fa cr] = [30 0 15 15]の場合、尤度からのp(hit)の推定値は0.98となる。これから計算したd'は2.10となる。

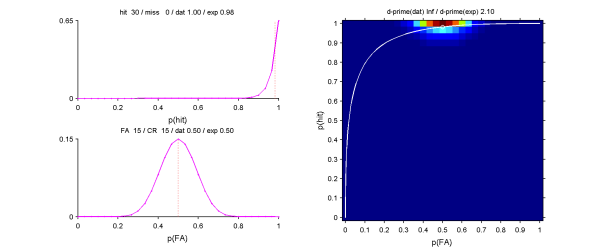
[hit miss fa cr] = [100 0 50 50]の場合、尤度からのp(hit)の推定値は0.99となる。これから計算したd'は2.53となる。だいたい満足した。

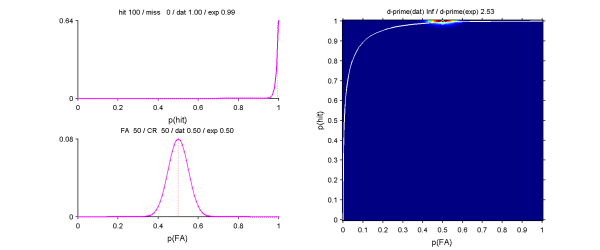
[100 0 0 100]とか極端な状態でd-prime(exp) = 5で、実際にはお手つきがあるから[99 1 1 99]でd-prime(exp) = 4。妥当なかんじ。ふつうのd'では>3とかに意味がないって言われるわけだけど、よっぽどそんなにでかいところまで発散しない。

matlabコードは http://pooneil.sakura.ne.jp/dprime_lik.m にアップしておきました。無保証でどうぞ。なんか間違いがあるようならぜひ教えてください。

■ SDTのd'にエラーバーつけたい。

SDTのd'にエラーバーつけたい。d'ってのはZ(hit) - Z(fa)だから、基本的にはp(hit)とp(fa)のエラーバーさえ付けられればよい。つまりこれは比率のデータにエラーバー付けたい、ってやつの応用問題だ。

それなら以前ブログ(20090319)で書いたとおり、最尤法で作れるはずだ。

---

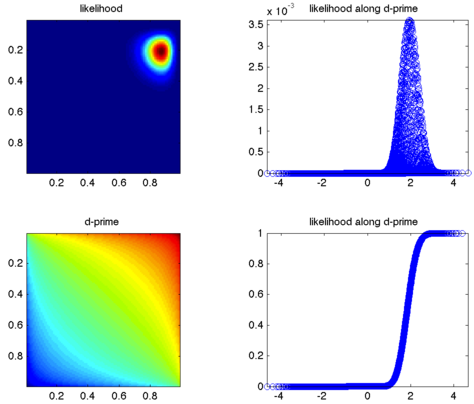
ということでやってみた。たとえばhit = 27, miss = 4, fa = 6, cr = 23というデータがあったとして、これのlikelihoodは、

Lik = p(hit).^hit .* (1-p(hit)).^miss .* p(fa).^fa .* (1-p(fa)).^cr;

となる。これを縦軸p(fa), 横軸p(hit)でプロットすると左上のようになる。おなじ軸でd'がどう変わるかをプロットすると左下のようになる。likelihood/sum(likelihood)をd'の小さい順に並べると右上のようになる。d'の軸では均等にサンプルされてないからこんなへんな図になるけど、これをcumulativeにしてやると右下のようになるので、とりあえず信頼区間を得るという意味では目的は果たせる。もっとましな方法はありそうだけど。

そっかあ、たぶん、左の二つの図をnorminv(p)の軸で作ればよいのだな。でも面倒だからやらない。

とここまでやってwebを調べてみたら、論文を見つけた。"A Comparison of Three Methods for Calculating Confidence Intervals around D-Prime" (pdf) ほかにもRによるimplementationを見つけた。

というわけで、自分でやるもんじゃねえよな、ってオチ。

■ Single-unit studyにGLMMは必要ないか？

前のエントリにVikingさんからコメントがありましたので、それへのレスポンスからいろいろ書いてみました。

Single-unit studyにはGLMMは必要ないだろうか？ まず現状として、だれかが必要だと主張しているわけでもない。JNPのガイドラインにもsubjectのnを増やしましょうなんてのはない。でも、いままでは問題とされてこなかったけど本当は問題だと思うんです。このあいだもいくつか書きましたし、二頭目でconsistentなデータが取れないで苦労した、なんてのはよく聞く話です。Subjectをrandom effectにできないのなら、他のsubjectに対するinferenceはできないのだから、そこで得られた知見はどちらかというと症例報告に近いということになります。(そのわりにn=1ではダメだってあたりが、社会的合意によって決まっていて、統計的裏付けがあるわけではない。) だからわたしが書いているのは、こういう問題を統計モデルとしてexplicitに扱いましょうよ、という問題提起だと思っていただければと思います。

どんな実験系もそれぞれに制約があります。fMRIだったらシグナルが非常に間接的なものであることだし、nhp single-unitだったら被験者が少ないことだし、multi-unitでのcoincedence detectionだったら記録時間が短いことだし。そのうえでみんなギリギリ言えることを主張するわけです。(high-quality journalになるほど無茶する必要が出てくる。)

でも統計的モデル化する際には形式上はみんな同じなんで、そういった実験側の制約を補償することは出来ないわけです。つまり、どんなにたくさんのneuronから記録しても、subject数=2であるならsubjectによる分散を推定することができないので(*)他の個体へのinferenceはいつまで経っても出来ません。「お前がそう思うんならそうなんだろう、お前ん中ではな」としか言いようがない。

(* GLMMのテキストをいくつか読んで理解したかぎりだと、subjectをrandom effectとしてとった場合には、モデルを作るときにはエラーの構造が変わるだけで、fixed effectのサイズの推定には影響しない。とりあえずmixed modelにするだけならsubjectのn=2でもできる。fixed effectのeffect sizeの推定値が得られると、その値を入れてやってMCMCとかやることでrandom effectのsize(=分散)の推定が出来る(経験ベイズ的な手法)。たぶんこの過程で、subjectのn=2だと正確な推定が不可能になるはず。subjectのnが少ないということの問題はこんなかんじで出てくる。)

以前のエントリで、せめてfixed effectでsubjectのinteractionが出ないことを示すべきだ、みたいなことを念頭に置いて書いたことがあります。でもこれだとSubject 1からcell 100個でsubject 2からcell 10個というデータだったとしてもバレません。

以前たぶんVikingさんのところにコメントしたけど消えちゃったんじゃないかと思いますけど、single-unit studyでは同じパラダイムでconsistentな論文が続いて出るかどうかでそういった分を担保しているように思うと書いたことがありました(*)。「階層ベイズをもっと体系的に組み込んで、実験系全体をモデル化するようなこと」って書いたときにイメージしていたのはそういうことで、メタアナリシスみたいに、複数の関連する実験結果をどんどん拘束条件に持ち込んでいって、そういった社会的合意みたいに済まされていたものをもっとexplicitにモデル化したらいいんじゃないか、なんて思うんです。

(* これはもちろんどの分野でも当てはまるのだろうけど、single-unitではかなりcriticalでないだろうか。)

それからもう一つ前提が抜けていましたが、いま言ったようなことはこれからの実験データのオープン化、データベース化、共有化という流れに向けて重要になるだろうと思ってます。これは2頭でnhpでsingle-unitというやり方自体を変えていった方がよいのではないかという問題提起も含むことになります。今書いていることの射程距離はそのへんです。

■ 「補正」が必要なのは、モデル化が不充分である証拠

超背伸びして書きました。怪しいところをwebで確認したりせずに書いた。もうしらない。厳しくせずに、褒めて伸ばしてほしい。

で、情報理論ってなんか嫌いなんですよね。っていうかニューロンの発火の解析関連での情報理論の応用ってのが嫌いってのが正しいのか。
なにがいやって、扱っているのがp(x,y),p(x)とか確率で、その計算をするのに使ったnが出てこない。基本的に無限試行行った後の理想的状態とかしか考えてないわけですよ。それは統計物理のようにものすごい多い数を扱っているときは良い。ていうかエントロピーって発想自体が元々そこからですからね。だけど、ニューロンの記録のように試行数10回とかでやっている事象にそのまま当てはめるわけにはいかない。
とは言いましたがもちろんわたしもITニューロンの発火パターンの解析に活用していようとか思っていろいろ勉強していたことがあったし、いくつか解析もしてました。そのころはちょうど
"Spikes: Exploring the Neural Code"が出た頃だったし、Panzeriの一連の仕事、たとえば
Golomb D, Hertz J, Panzeri S, Treves A, Richmond B. "How well can we estimate the information carried in neuronal responses from limited samples?" Neural Comput. 1997 Apr 1;9(3):649-65.
(ちなみにPanzeriはさいきんもStefano Panzeri, Riccardo Senatore, Marcelo A. Montemurro and Rasmus S. Petersen "Correcting for the Sampling Bias Problem in Spike Train Information Measures" J Neurophysiol 98: 1064-1072, 2007ってレビューを出してるのを知った。)
とかを読んだり、菅生さんのNature
Sugase Y, Yamane S, Ueno S, Kawano K. "Global and fine information coded by single neurons in the temporal visual cortex." Nature. 1999 Aug 26;400(6747):869-73.
が出た時代で、これのインパクトは大きかった。
んで、けっきょくのところ、少ない試行数だと、試行間のvariationの分だけ情報をoverestimateしてしまいます。(音A刺激の試行と音B刺激の試行とで視覚野ニューロンのスパイク数を数えれば、試行間のばらつきがあるから、相互情報量>0となってしまう。) だからその分の補正をしようってのが上述のGolomb et.alとか含めていくつか仕事があるわけです。
そのころは相互情報量ってけっこう扱いにくいなあとかそのくらいに思ってたんだけだけど、その後の業界的にも「選択性の指標」みたいなかんじで相互情報量を使うってのはあまり見なくなってきたし、私もすっかり忘れてました。(いまだにノンパラでの分離度としてROCのd'とかAUCとか使うのは多いんだけど、あれはなんなんだろ。自分でも使ってるけどね。)

んでずっと放置してたんだけど、この「補正」という発想がポイント(ガン、って書こうと思ったけど、これっていまどきpolitically incorrectですかね)なんではないかと思ったんです。つまり、「補正」が必要なのは、モデル化が不充分である証拠。

一つの例はあれですね、fMRIでのvoxelごとに検定をすることによるmultiple comparisonの問題を、Bonferroniの「補正」を使うのではぜんぜんpracticalでない(補正が効き過ぎる)のを、Worsley-Fristonがrandom field theoryという、voxelのデータにsmoothingがかかったものを明示的にモデル化した理論を使うことによって解決したわけです。これによってfMRIの解析のスタンダードが確立したと言えると思います。

もうひとつ例を挙げると、時系列データの解析(たとえばLTPの時間経過の検定とか。それともいまだに時点ごとのt検やってんのかな)では、repeated measures ANOVAがよく使われますが、球面性の仮定が成り立たない場合、自由度に「補正」をかけます(Greenhouse-GeisserのεまたはHuynh-Feldtのε)。つまりじっさいのデータの数から計算した自由度では自由度をoverestimateしてしまうから、自由度を下げてやっているわけです。
こちらのほうの問題はけっきょく、球面性の仮定を行っていないMANOVAを使うことで解消されました。つまり、モデル内で要因間の差の分散が違っていることをを想定していないrepeated measures ANOVAで、要因間の差の分散が違っている分の補正をかける、なんてトリッキーなことをせずに、残差の共分散構造をあらかじめモデルに取り込んだMANOVAを使うほうがstraightforwardなわけですから。(じっさいにはMANOVAはデータ数が少ないと使えないとかいった弱点がありますが：反復測定 ANOVA か、(G)MANOVA かの選択の問題 ) General linear modelからgeneralized linear modelへの拡張によって問題が解決した、というのが正しい言い方でしょうか。

んで、翻って、おなじような解決法が「ニューロンの発火の解析関連での情報理論の応用」でも見られないかなと思うんです。ここはたぶんベイジアンですよね。というのも、「少ない試行数だと、試行間のvariationの分だけ情報をoverestimateしてしまう」というのは、fittingにおけるoverfittingの問題とたぶん等価もしくは相似ですよね。(PRML本の第一章読んだのでかぶれてる…) Overfittingの場合も、データのnが少ないときに推定値の分散を考慮していないためにバイアスが出る、というのが元凶でした。
ペナルティの項を与えるっていう発想はちょっと「補正」の発想に似ていていやな気はするけど、試行数を明示的に入れた上で相互情報量やKL-divergenceのことを考える、というとベイジアン的な取り扱いをするということになりますよね。そういうのってあるんだろうか。たぶんあるんでしょう。よく知らないけど。なかったら作るべきだ。相互情報量の「補正」なんかしてないで、このレベルから捉え直すべきだ。たぶんbinの問題(binの存在を前提としていること、binの中に必ずデータが入っているようにbinを切らないといけない)もここで解消すべき問題なんではないかと思います。

そもそもわたしの分野で、真の意味で情報理論的取り扱いをする必要がある部分はどこにあるのか(反応選択性の指標代わりとかぢゃなくて)、というあたりが問題だったりもします。ただ、これからBMIとか大規模データ集積とかそういうところが発展していくことによって、たぶん必要なデータ解析自体は変わってくることになります。もともとこのfieldは、subjectのn=2で、記録ニューロンの数がm=100とかそういった歪んだ状況でANOVAとかGLMとかやってきたわけでそれはおかしな話でした。次へ進むためには、そのへんは整備されないといけない。これがわたしの仕事だとは思わないのだけど、上記のFristonがfMRIで行った業績のように、だれかが手がける必要がある問題なんじゃないかと思ってます。

落ち穂拾い：nをものすごく大きくするとなんでも有意になってしまうという問題があります。けっきょくこれはp-value至上主義の弊害であって、ホントはtype I errorとtype II errorとでのpayoffを考えるべきなんですよね。

■ 適合度の尤度比検定ってこれで良いの?

(追記：latexでPDFファイルを作成しました。そちらの方が数式が読みやすいかと思います。こちらから：loglikelihood.pdf)

宿題持ってくるんじゃねー、とか言われたりしないのでブログは良い。
以下の問題を解こうとして、ネットを調べてたんですが、よくわからないので自作してみました。これでいいんでしょうか、先生(<-だれよ)：

こういう問題です：
Observed dataがN個あってそれのヒストグラムを作りました。
このヒストグラムをfittingしてやるために二種類のモデルによるヒストグラムを作りました。
モデルH0とモデルH1があって、H1はH0のモデルにパラメータをひとつ付加したもの。それぞれのモデルからデータをgenerateしてやって、ヒストグラムを作る。
モデルH0によるfittingの適合度とモデルH1によるfittingの適合度とを比べて有意差があるか知りたい。
そこで、ふたつの適合度の尤度比検定をしてやろうというわけです。
それぞれのfittingの尤度関数さえ計算できれば、モデル間で差がないとする帰無仮説において「-2*loglikelihoodの差」が自由度1(H0とH1での自由度の差)のカイ二乗分布に従うことを使って検定できます。
(なお、全部ヒストグラムではなくて確率密度関数にしても成り立つはず。あと、要はモデル選択なので、AICとかBICでやるかという話もあるけど、とりあえず簡単のため尤度比検定で。)

Obserbed dataはN個：

[data(1),data(2),data(3),....data(N)]

ヒストグラムのbinはn個：

[x(1),x(2),x(3),....x(n)]

Observed data、
モデルH0でのbest-fitted data、
モデルH1でのbest-fitted data、
のそれぞれのヒストグラムでの各binの頻度：

[ NO(x(1)), NO(x(2)),..., NO(x(n))]
[NE0(x(1)),NE0(x(2)),...,NE0(x(n))]
[NE1(x(1)),NE1(x(2)),...,NE1(x(n))]

それぞれのヒストグラムのデータの総数は

∑( NO(x(i)))=N
∑(NE0(x(i)))=N
∑(NE1(x(i)))=N

です。(Fitting時に同じになるようにnormalizeしてある。)

まずそれぞれのfittingの尤度関数を作ってみる。
まずObserved dataのある1個data(j)がヒストグラムのbin x(i)に落ちるとすると、
data(j)がモデルH0の分布のbin x(i)に落ちる確率は

NE0(x(i))/∑(NE0(x(i)))=NE0(x(i))/N

と書けます。
だから、尤度関数L(H0)は全observed dataの数だけこれを掛け合わせたものです。
Observed dataの[data(1),data(2),data(3),....data(N)]
がそれぞれ落ちるbinがたとえば
x(m),x(n),x(q),x(r)
とかだとすると、

L(H0)=(NE0(x(m))/N)*(NE0(x(n))/N)*(NE0(x(q))/N)*...*(NE0(x(r))/N)
=NE0(x(m))*NE0(x(n))*NE0(x(q))*...*NE0(x(r)/(N^N)

といったかんじになります。
これをlog-likelihoodに変換すると、

LL(H0)=ln(NE0(x(m)))+ln(NE0(x(n)))+ln(NE0(x(q)))+...+ln(NE0(x(r))-N*ln(N)

です。
全observed dataはx(i)のbinのどこかに落ちるから、
たとえば、x(1)のbinに落ちるobserved dataはNO(x(1))個ある、というふうに整理すると、

LL(H0)=NO(x(1))*ln(NE0(x(1)))+NO(x(2))*ln(NE0(x(2)))+...+NO(x(n))*ln(NE0(x(n)))-N*ln(N)

となります。これを∑を使ってbinごとに(i=1:n)足し合わせるように表記すると

LL(H0)=∑(NO(x(i))*ln(NE0(x(i))))-N*ln(N)

と書けます。
同様にH1のモデルのときは

LL(H1)=∑(NO(x(i))*ln(NE1(x(i))))-N*ln(N)

となります。
あとは2LLを作るだけ。二番目の項が消えます。

2LL = -2*(LL(H1)-LL(H0))
=2*∑(NO(x(i))*ln(NE0(x(i))))-2*∑(NO(x(i))*ln(NE1(x(i))))

∑はどちらも共通のbin x(i)で足し合わせているから合体できます。

2LL = 2*∑(NO(x(i))*ln(NE0(x(i))/NE1x(i)))

ということで計算できました。
これで合ってるのか答えがネットを探していても見つからないのだけれど、G-testやKL diveregenceの値と似ているから、間違った方向には行ってないでしょう。ということで検算のためにG-testの式に近づけてみる：
上記の2LL式を変形してやると、

2LL= 2*∑(NO(x(i))* ln(NE0(x(i))/NE1(x(i))*NO(x(i))/NO(x(i))))
   = 2*∑(NO(x(i))*(ln(NE0(x(i))/ NO(x(i)))-ln(NE1(x(i))/ NO(x(i)))))
   =-2*∑(NO(x(i))*(ln( NO(x(i))/ NO(x(i)))-ln( NO(x(i))/NE1(x(i))))
   = 2*∑(NO(x(i))*(ln( NO(x(i))/NE1(x(i))))-2*∑(NO(x(i))*(ln(NO(x(i))/NE0(x(i))))
   = G(H1)-G(H0)

となって、二つのG検定値の差となっています。なんてこったorz
ちなみにモデルH0でobserved dataをfittingしたときのG検定のG-statisticsは、

G（H0)=2*∑(NO(x(i))*(ln(NO(x(i))/NE0(x(i))))

となります。

というわけでたぶんこんな長々と計算しなくても、二つのfittingをして、G-statisticsを計算して、その差をカイ二乗検定すれば良かったというオチ、のようです。じつははじめに計算をしたときは、G statisticsではなくてカイ二乗の方を使ったのだけれど、カイ二乗の差をまたカイ二乗検定、ってなんかへんではないか?と思って上のような計算をしてみた次第。あと、G-test自体がobserved dataとfitted dataとのあいだでの尤度比検定なのは知っていたのですが、二つのモデルの比較で単純にそれらをさし引いて良いかどうかがわからなかったわけです。以上の計算からすると、最尤推定の考えからしてもさし引いて良い、ということになりそうですが。

ま、いつも通り自分で疑問出して自分で納得してるってかんじなのですが、まだ納得しているわけではないんです。というのも、計算される値が大きすぎるし、ググっても、関係してくる項目が見つからない。まだなんか間違えている気がします。

また、G検定はいわばKL divergenceの離散バージョンと式の上では同じですから(ところでこのことをwebで探しても明確に書かれているものを見つけられない)、情報幾何で使われるイメージ化の方法が使えます。ここでしている-2LLのカイ二乗検定というのは、[Observed data -> model H0でのbest fitted data]の距離と[Observed data -> model H1でのbest fitted data])の距離との差を取っているということになります。たとえば「神経回路網とEMアルゴリズム」とかにあるようなとり扱いをすると、observed dataの集団を多様体の中のある一点として、H0のモデルに属した曲面とH1のモデルに属した曲面とがあって、observed dataの点からそれぞれの曲面に垂線を下ろした当たったところがそれぞれのモデルでのbest-fitted dataの集団の位置で、その垂線(正確にはm測地線)の距離がKL-diveregenceです。

さて、そうするとわたしがわからないのは、そういったまっすぐでない空間での二つのKL-divergenceをたんにさっ引いてよいのかっていう問題になるのかも知れません。ていうかそこまでいくと、2LLの原理を調べろ、ってことでネイマンーピアソンまで戻って勉強しないといけない。こういうことやってるとJSTORにある昔の統計学の論文とか読み出してどんどんはまることになるので、このへんまでにしておきます。

■ テンパってます：MATLABのspline()

過去日記は続くよどこまでも：

なんでMATLABのyi=spline(x,y,xi)はxが単調増加もしくは単調減少でないと使えないんだよ！ 使えてると思ったらたんにxを勝手にソートされてたよ！ あぶねー。

xx=[1:5 4.5]
yy=[2:7]
xxi=1:0.2:5;
yyi=spline(xx,yy,xxi);
figure
hold on
plot(xx,yy,'bx-')
plot(xxi,yyi,'ro-')

Linearのinterpolation(interp1)でも同じ。Linearのinterpolationだったら、んな問題、本質的じゃないじゃんか。2点ありゃ計算できるんだから。あと、

xx=[1:5 5]
yy=[2:6 6]

とかにしておくと、"The data sites should be distinct."とか文句言いやがる。んなもん、隣り合ってる点が同じだったら取り除いて計算すりゃいいじゃんか。

……とソフトにあたる私。

追記：冷静になりました。つまり、発想が違うのでしょうな。順序の概念を前提としていない、と。あと、y=f(x)でinterpolationをするということからして、xによってyが一意に決まるようでないとおかしい、という筋もあるのかもしれない。(xとyとが対照でないのですな。)

でも、x=[1 0 -1 0]とy=[0 1 0 -1]から円を描く、というサンプルプログラムでわざわざ極座標に変換してから補完するくらいなら、順序の概念を使えばよい気もするのだけれど。

■ Smallest Enclosing Ellipse

ある複数の点を包含するような最小の面積を持つ楕円を決定するにはどうすればよいかと調べたことがあったんですが、けっきょく"Smallest Enclosing Ellipse"というのがキーワードなのだということにやっとたどり着いたのでした。んでそのときのブックマークを見つけたので、リスト作成しときます。

• Bounding Containers for Polygons, Polyhedra, and Point Sets (2D & 3D)
• Smallest Enclosing Balls of Points
• Rotating Calipers
• 2D Smallest Enclosing Ellipse
• Smallest Enclosing Ellipses - An Exact and Generic Implementation

■ Implicit perception and signal detection theory

Nature Reviews Neuroscience 6, 247-255 (2005); doi:10.1038/nrn1630 "IMAGING IMPLICIT PERCEPTION: PROMISE AND PITFALLS" Deborah E. Hannula, Daniel J. Simons and Neal J. Cohen
Awarenessがないにもかかわらず、知覚情報処理ができている、というimplicit perceptionにはmasking刺激を使ったものなどいろいろありますが、imagingのstudyなどでは被験者にawarenessを報告させる(提示した刺激が見えたかどうか)ことでawarenessの程度を評価することがしばしばあります。しかし被験者によるverbal reportに頼るこの方法は被験者が「見えた」と判断するバイアスが大いに関わってきて適切ではありません。これがタイトルの'pitfall'というやつ。そこで心理物理学者はどうするかというと、信号検出理論を使ってこのようなバイアスを取り除いた感度(d')をimplicit条件とexplicit条件とで比較してやるわけです。
つまり、explicit条件でd'=0であるにもかかわらず、implicit条件でd'>0であること、これがimplicit perceptionのよりobjectiveなcriteriaである、というわけです。
しかしこのようなアプローチはまだcontroversialで、たとえば以下のような議論があります。
Perception & Psychophysics, Volume 61, Number 5, 1999, pp. 986-992 "A signal detection theory analysis of an unconscious perception effect"(pdf; open access)(*) STEVEN J. HAASE, JOHN THEIOS AND RICK JENISON
を受けて書かれたこの論文
Perception & Psychophysics, Volume 66, Number 5, 1 July 2004, pp. 846-867(22) "Unconscious perception: A model-based approach to method and evidence" Michael Snodgrass; Edward Bernat; Howard Shevrin
とそれに対するコメンタリおよびその返答：
Perception & Psychophysics, Volume 66, Number 5, 1 July 2004, pp. 868-871(4) "Valid distinctions between conscious and unconscious perception?" Steven J. Haase; Gary D. Fisk
Perception & Psychophysics, Volume 66, Number 5, 1 July 2004, pp. 872-881(10) "Unconscious perception: The need for a paradigm shift" Daniel Holender; Katia Duscherer
Perception & Psychophysics, Volume 66, Number 5, 1 July 2004, pp. 882-887(6) "Unconscious perception and the classic dissociation paradigm: A new angle?" Eyal M. Reingold
Perception & Psychophysics, Volume 66, Number 5, 1 July 2004, pp. 888-895(8) "Unconscious perception at the objective detection threshold exists" Michael Snodgrass; Edward Bernat; Howard Shevrin
それから、同じようなメンバーでConscious and Cognitionを舞台にしたもの：
Conscious Cogn. 2004 Mar;13(1):73-91. "Subliminal perception and its cognates: theory, indeterminacy, and time." Erdelyi MH.
Conscious Cogn. 2004 Mar;13(1):92-100. "Availability, accessibility, and subliminal perception." Kihlstrom JF.
Conscious Cogn. 2004 Mar;13(1):101-6. "Inaptitude of the signal detection theory, useful vexation from the microgenetic view, and inevitability of neurobiological signatures in understanding perceptual (un)awareness." Bachmann T.
Conscious Cogn. 2004 Mar;13(1):107-16. "The dissociation paradigm and its discontents: how can unconscious perception or memory be inferred?" Snodgrass M.
Conscious Cogn. 2004 Mar;13(1):117-22. "Unconscious perception: assumptions and interpretive difficulties." Reingold EM.
Consciousness and Cognition Volume 13, Issue 2 , June 2004, Pages 430-433 "Comments on commentaries: Kihlstrom, Bachmann, Reingold, and Snodgrass" Erdelyi MH.
Conscious Cogn. 2004 Sep;13(3):613-8. "Subliminality, consciousness, and temporal shifts in awareness: implications within and beyond the laboratory." Bornstein RF.
また、これらに関連して
Consciousness and Cognition Volume 10, Issue 3 , September 2001, Pages 294-340 "Confidence and Accuracy of Near-Threshold Discrimination Responses" Craig Kunimoto, Jeff Miller and Harold Pashler
Am J Psychol. 2002 Winter;115(4):545-79. "Disambiguating conscious and unconscious influences: do exclusion paradigms demonstrate unconscious perception?" Snodgrass M.
Am J Psychol. 2005 Summer;118(2):183-212. "Unconscious perception or not? An evaluation of detection and discrimination as indicators of awareness." Fisk GD, Haase SJ.
また、哲学者のNed Blockも
Trends in Cognitive Sciences Volume 9, Issue 2 , February 2005, Pages 46-52 "Two neural correlates of consciousness" Ned Block
でPhenomenal consciousnessとAccess consciousnessとの分離する試みに信号検出理論を使う例として
Journal of Experimental Psychology: Learning, Memory, & Cognition. 1994 Mar Vol 20(2) 304-317 Unconscious perception: Attention, awareness, and control. Debner, James A.; Jacoby, Larry L.
でのexclusion paradigmを挙げたり(これは上記Nature Reviews Neuroscience論文でもreferされてます)、Lammeの
Nature Neuroscience 4, 304 - 310 (2001) "Two distinct modes of sensory processing observed in monkey primary visual cortex (V1)"
を説明してたりします。

(*) いつも忘れるんだけれど、Perception & Psychophysicsは現在2002年までfreeでfull textにアクセスできます。2001-現在へのリンク、それから、1991-2000年のtextの検索ページ。

■ モンテカルロ(2)

昨日のつづきを貼ります：

---

昨日のコードを使って、どのくらいのループ回数でどのくらい真の値に収束するか確認してみました。

mloop=1000;sloop=5;loop=10^sloop;
data2=zeros(log10(loop),2*mloop);
nummat=10.^(1:sloop);
tic;
for m=1:mloop
	n=randn(1,1);meanN=n;meanNp=n;ssN=0;ssNp=0;stdN=0;
	data=[];
	for i=2:loop
		n=randn(1,1);
		meanN = (meanNp*(i-1)+n)/i;
		ssN = ssNp + (i-1)*(meanNp^2) -i*(meanN^2) + n^2;
		stdN = sqrt(ssN/(i-1));
		meanNp=meanN;ssNp=ssN;
		if ~isempty(find(nummat==i))
			data=[data;i meanN stdN];
		end
	end
	data2(:,2*m-1:2*m)=data(:,2:3);
end
toc;
k1=log10(abs(data2(:,1:2:size(data2,2)-1)));
k2=log10(abs(1-data2(:,2:2:size(data2,2))));
figure
hold on
plot(log10(nummat),median(k1'),'ro-')
plot(log10(nummat),median(k2'),'bo-')

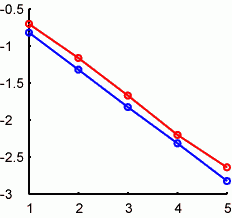
横軸がループの回数(log10(x))。縦軸は計算された値と真の値との差（絶対値）をlog10スケールにて。赤が乱数のmeanによるもので、abs(mean(data))で、青が乱数のsdでabs(1-std(data))です。昨日の計算を10000回繰り返して横軸の各点でのmedianをとっています(非対称分布なのでmean is not = median)。Meanとsdのどちらも直線近似できて、slopeは1/2なのです。これはたぶん差の絶対値だからで、差の二乗を取ればslope=1になったのでしょう。

以上の計算をしなくてもなんかのやり方で導出できるのでしょうけれど（そういうのってなにを読めばわかるのだろうか）、こういうことがわかりました：ループの繰り返し回数を10倍にすると真の値からのズレはsqrt(1/10)=1/3.16だけ小さくなる。

---

ところでこういうことやってよいか。とくに端数の問題、浮動小数点の問題。全データを用意しておいて､全データで一挙に計算したときとループごとに計算したときで誤差がどのくらいあるか検証してみる。

---

なんてことを考えて放置したままになっていたのでそのまま貼っておきます。

■ モンテカルロ(1)

昨年くらいに途中まで作って放置してあったエントリを貼っておきます。しかも「間違ってる！」なんてメモまで付いてる。なんだったか忘れたので埋め草用に。しかも明日に続きます。

---

モンテカルロでなんかの値のmeanとsdとを計算するために10万回とかループを回して、全部の値を行列に収納してからそれのmeanとsdとを計算していたのですが、それではおっつかなくなってきたので、ループごとにmeanとsdとをアップデートしてゆくような漸化式の形を作るようにしました。そんなことすらサボってたわけです。

平均：MEAN; 変動(sum of square)：SS; 標準偏差：SD; として、
MEANn = (MEANn-1 * (n-1) + newdata )/ n
SSn = SSn-1 + (n-1) * (MEANn-12) - n * (MEANn2) + newdata2
SDn = sqrt(SSn / (n-1) )

たとえば、randnでmean=0、sd=1の正規分布の乱数を生成させるのを10^8回繰り返してその乱数のmeanとsdを計算してやると、

tic;
nummat=10.^(1:8);data=[];loop=10^8;
n=randn(1,1);meanN=n;meanNp=n;ssN=0;ssNp=0;stdN=0;
for i=2:loop
	n=randn(1,1);
	meanN = (meanNp*(i-1)+n)/i;
	ssN = ssNp + (i-1)*(meanNp^2) -i*(meanN^2) + n^2;
	stdN = sqrt(ssN/(i-1));
	meanNp=meanN;ssNp=ssN;
	if ~isempty(find(nummat==i))
		data=[data;i meanN stdN];
	end
end
toc;

figure
hold on
plot(log10(data(:,1)),data(:,2),'ro')
plot(log10(data(:,1)),data(:,3),'bo')

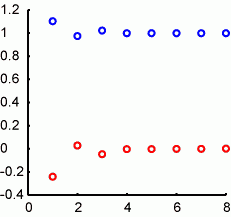
わたしのノートPCではelapsed_time =18975secで計算されます。図の通り、横軸がループの回数(log10(x))。縦軸がそれぞれのループの回数で計算された値で、赤が乱数のmeanで、回数が増えるほどに0に近づきます。青が乱数のsdで、回数が増えるほどに1に近づきます。10^5=10万回くらいやればだいたいよさそうなことがわかります。

ほんとうはもっと良いのは、matlabが得意とする行列での演算と組み合わせることで、

std(randn(10^4,10^3));
elapsed_time =	2.0160

なんてので10^4個の乱数のsdが10^3個計算できるので、それを前述の漸化式のように組み合わせたほうが10^7個の乱数のsdを計算するのはもっと速くなることでしょう。ちなみに直で計算させると

std(randn(10^7,1));
elapsed_time =  165.8200

メモリーが圧迫されるのでけっこう時間がかかってしまいます。さらに、うちのノートPCではもう一桁増やすと

std(randn(10^8,1));
??? エラー: ==> randn
メモリが足りません.HELP MEMORYとタイプしてオプションを確認してください

なんて出てきて、もう計算できません。

■ JNP 統計の使い方のガイドライン

つづき。
…こんな感じです。信頼区間の表示、というのにはちっと違和感を感じました。上でも書きましたけど、図としての表示の仕方にそぐわないのですね。この調子で行くなら、2-way ANOVAはfittingしたモデルによる成分と残差プロットとを別々に出してやる必要がある、ってぐらいのところまで行ってしまいます。
se or sdが重要な問題であるのは間違いない。seはデータ数nさえ増やしてしまえばどんどん小さくなってゆくので、どんなに生理学的or薬理学的にしょぼいデータでもnを増やして有意差をつけることはできるのです。たとえばある薬がある生理学的数値を0.01%上昇させるだけだったとしても、nが増えれば有意差が必ず出せます。よって、どのくらいの変動があれば生理学or薬理学的に有意味であるか、ということを判定する必要があるのです。
一方で、fMRIのデータというのはまさに1%とかのシグナル変動を、nを加算したり、時間的空間的相関をフル活用したりして、その有意度を検出してくるのですね。じゃあ、それはまずいのかというとそうではなくて、fMRIでのBOLDシグナルというのは、神経活動によって間接的に変動を受けるものなので、その変動が小さくなってしまうのは仕方ないわけです。たとえば、脳のあるvoxelの中のニューロンの10%が普段の10倍発火したとして、それによって起こるBOLDシグナルの変動はニューロンによるものよりもずっと小さく、しかもtime courseも遅い、だからこそ1%の変動に有意差を出す意義があるわけです。
というわけで、けっきょく、そういった生理学的有意味度という価値判断がないと、われわれは有限のデータから得られた統計結果でなにかを言うことをできない、って極論ですな。αだけでなくてβも考慮すべき、ということは言えるのではないでしょうか。なんにしろ、そもそも二つのグループの分布が重ならないくらい離れているなら、統計なんてなくても一目瞭然。だから、これは定量的か、定性的か、なんて問題でもあります。
なお、このへんに関する重要な論文の抄録が"TAKENAKA's Web Page: 有意性検定の無意味さ"にあります。
ついでに：私がガイドラインに手を加えるなら、こんなこと（(1)(3)に含まれますけどね）：
(A) Subjectのeffectを考慮すべし。とくにsingle-unitなら、animal間で結果がconsistentであることを示すべき。私たちの分野ではsubjectの数はせいぜい2-3なので、これらの間でconsistentでないデータは、main resultにはなりえない。Animal consistencyを示していないデータはほとんどがどちらか一匹のデータに依存していると見なされてもしかたない(これでJNPのsingle-unit論文のデータのほとんどは失格する)。
(B) 正規性の仮定に敏感になるべし。正規性の仮定が成り立たないものでt-testやANOVAをしてはいけない。たとえ、ANOVAに頑強性があることが知られていたとしても。たとえば、サッケードのreaction timeはその逆数が正規分布することが知られています（以前扱ったCarpenter論文を参照）。よって、解析をするときには逆数取ってからそれでANOVAするべきなのです。そんな論文見たことないけど。
私は以前、比のデータA1/B1とA2/B2とをANOVAで検定したことがありますが、正規性がまったく仮定できないので、これに対処するために私は統計学の雑誌をあさって、ノンパラバージョンの2-way ANOVA (Friedman testは繰り返しの回数が同じでないと使えないし、interactionがないことを仮定しているのでダメ）を自作したことがあります。けっきょくは使わなかったのですが、ANOVAでの結果とそんなに大きくは変わらない印象がありました。本当はあの解析はA1-A2とB1-B2という二つのfactorがあって、それの間でのintractionとして検出すべきだったのでしょう。尤も、こんなことをうるさくいう人間は私しかいなくて、reviewの過程でそういうことを指摘されたことは一回もなかったのですが（意味ねー）。
(C) 回帰分析では外れ値がものすごく効いてくるので、てこ比やCoock distanceなどの指標を添えてrobustnessを評価するべき。
…だんだん話が細かくなってきましたが。
では最後に関連論文。

• Statistics in Medicine '00 "Statistics in medical journals: some recent trends."
• J Appl Physiol "Fundamental concepts in statistics: elucidation and illustration." 今回の著者の前報みたいなもん。
• British Journal of Anaesthesia '03 "Misuse of standard error of the mean (SEM) when reporting variability of a sample. A critical evaluation of four anaesthesia journals."

■ JNP 統計の使い方のガイドライン

いつもどおりサッポロ一番塩ラーメンをラボのお茶部屋で作って食べながらJNPをぴらぴらめくっていたら、重要そうなのがあるではないですか。こういうことがあるから紙のジャーナルを置いておく価値があるってもんですよ。

JNPのeditorialより。

"Guidelines for reporting statistics in journals published by the American Physiological Society."

JNPを出版しているAmerican Physiological Societyが統計の使い方についてのガイドラインを出しています。簡単にまとめ。

1. 実験を計画する際に(使うべき統計などに)不明な点があったら統計学者に相談すること。
2. 有意度水準αは目的にあったものを選んでそれを明示し、正当性を与える。
3. どういう統計方法を使ったか、どういう統計パッケージを使ったかをわかるようにしなさい。
4. 多重比較を統制しなさい。
5. (5) データのばらつきはseではなくてsdを使って示しなさい。
6. 見出した統計結果の不確かさは信頼区間を使って示しなさい。
7. 正確なP-valueを示しなさい(P<0.05ではなくてP=0.023とか)。
8. 統計結果の数字には科学的に意味のある有効数字までを表示しなさい。
9. 要旨ではmain resultのそれぞれに正確なP-valueと信頼区間を示しなさい。
10. Main resultのそれぞれの解釈には正確なP-valueと信頼区間を用いなさい。

私の印象というかコメント：

(2)に関して、P<0.05を無差別に使うのはよくないとして、P<0.01やP<0.10を使った方がよいことを示しています。たしかに、0.05<P<0.10に位置するものはpotentialには帰無仮説がrejectされる可能性があるものといえますが（ゆえに、有意でないときはP>0.10であることを示さないと、例数が足りなくて有意に出なかっただけではないかと疑われる）、もし論文のmain resultのPがα=0.10で書いてあったらかなり信頼性落ちると思います。しかもそれが(3)の問題をviolateしていて、たとえばsubject間のばらつきを考慮せずに単にノンパラとかの比較をしているとしたら、私だったら認めないです。

(4)は私がこの場で何度も書いていることです。実際にはかなりややこしい問題があることもこれまで述べた通り。

(5)、これなんですが、データのばらつきはたとえばsingle-unitの論文のtableとかではすでにみんなstandard deviationの方を使っていると思うのですよ。その一方で、平均値の比較とかで使うエラーバーはみんなseを使っていますよね。それはもちろん、平均値の比較をしたいときにはそのグループのデータの平均値のばらつきを見たいからであって、データ自体のばらつきを見たいわけではないからなのです。このようなseの使い方には問題がないと思うのですがね。このへん、ガイドラインではどう考えているのだろう、というと：

(6) seではなくて、平均値の信頼区間の方を使え、ということのようなのですね。たとえば、multipe regressionとかでの個々のb (それぞれのregressorのcoefficient)を評価するのに信頼区間を使う(bの信頼区間が0にかかっていないことを示す)、というのはいいと思うんだけど、上述の平均の差の検定のときはどうすればよいんだろう？ 平均の差の信頼区間を作ってそれが0にかかっていないことを示す？ とりあえず、conventionalなbar chartにエラーバーという図にはまったく馴染まないですが。

(7) 私はいままでP=0.019とかいう書き方をしてきましたが、有意でない方に関してはP>0.10とかF<1とかでよいと思うんです。P>0.90とか書いているのを見かけることがあって、それって片側検定してるせいじゃん、とか思ったりしますけど。 …こんな感じです。明日続き貼ります。

■ Psychometric functionの書き方

やっとわかった。こんなこともわからないでいたのです。Psychophysicsの基本中の基本にもかかわらず。

Psychophysicsではdetectionの閾値を決定するのにpsychometric functionを書きます。たとえば図のようなものです。たとえば、二つのターゲットのどちらかが点灯するのでどっちが点灯しているか当てなければならないとします。横軸はターゲットの明るさで、右が明るくて左が暗くなります。縦軸は正答率です。ターゲットのコントラストが明るいときには正答率はほぼ1ですが（右側の青丸）、暗くなるとどっちが点灯しているかわからなくなるので正答率はchance levelの0.5まで落ちます（左側の青丸）。これをlogistic regressionによってfittingしてやって、縦軸の0.75を通るところをその人の検出能の閾値としてやるわけです。しかしlogistic regressionというのは普通は縦軸が0-1の範囲を動くものなので、二択の時にはそれを0.5-1の範囲を動くようにmodifyしてやらなければならないのですが、そのやり方がよくわからなかったのです。

そこで参考サイト："Matlab and Sas logistic"

というわけで、matlabでglmfitを使い、inline関数でfittingしたい関数の形を設定してやればよかったのです。

そこでまず、inline関数で2択(2AFC: two alternative forced choice)、四択(4AFC: four alternative forced choice)、yes-no question (正答率0-1の範囲)のそれぞれの場合のlink関数を設定してやります。

function mylink = choose_link(choice)
% choose link function
% 0:yes-no 0-1;
% 2: 2AFC 0.5-1;
% 4: 4AFC 0.25-1

switch(choice)
  case 1,
    mylink='logit';
  case 2,
    fl=inline('log( (max(0.5+1e-6, min(p, 1-1e-6))-0.5) ./ ...
                 (1-max(0.5+1e-6, min(p, 1-1e-6))))')
    fd=inline('(1-0.5) ./ ( (1-max(0.5+1e-6, min(p, 1-1e-6))) .* ...
                  (max(0.5+1e-6, min(p, 1-1e-6))-0.5))')
    fi=inline('(0.5 + exp(x)) ./ (1+exp(x))') 
    mylink={fl fd fi};
  case 4,
    fl=inline('log( (max(0.25+1e-6, min(p, 1-1e-6))-0.25) ./ ...
                 (1-max(0.25+1e-6, min(p, 1-1e-6))))')
    fd=inline('(1-0.25) ./ ( (1-max(0.25+1e-6, min(p, 1-1e-6))) .* ...
                  (max(0.25+1e-6, min(p, 1-1e-6))-0.25))')
    fi=inline('(0.25 + exp(x)) ./ (1+exp(x))') 
    mylink={fl fd fi};
end

これをchoose_link.mとして保存しておいて、

dat=[0.6021  4  9
     0.6990 12 25
     0.7782  8 14
     0.8451 14 16
     0.9031 11 11
     1.0000  9  9
     1.0792 11 11
     1.1761 10 10];

% [x y Ny]   variable success total
x =dat(:,1);
y =dat(:,2);
Ny=dat(:,3);

mylink = choose_link(2);
[b,dev,stats]=glmfit(x,[y Ny],'binomial',mylink);
xx=min(x):(max(x)-min(x))/100:max(x);
yfit = glmval(b,xx,mylink);

figure
hold on
h1=plot(x,y./Ny,'o');
h2=plot(xx,yfit);
set(h1,'markersize',10)
set(h1,'linewidth',2)
set(h2,'linewidth',2)

データ(dat)からlogistic regressionしてやると図のようなpsychometric functionが書けるという訳でした。

もう少し説明しますと、入力するデータdatとして、一列目がvariable (横軸として振った値)、二列目がsuccess trial数、三列目がtotal trial数という行列を用意します。これをglmfitに入れるわけですが、logistic regressionでは四番目の引数にリンク関数を入れる必要があります。これが'logit'なのが普通の0-1の範囲を動くデータでのlogistic regressionです。そこでchoose_link functionでこのリンク関数をinline関数mylinkとして設定してやるとregressionができて、coefficient bが出てくるのでこれでデータの範囲を100等分した新しい横軸のデータでglmvalを使ってfittingの値を得る、というわけでした。

何とかここまで来れましたが、要するにわたし、inline関数とかeval関数とかのような文字列を評価して計算する、というのがいまだによくわかってないのですね。

glmfitのhelpにたしかに関連することが書いてあるのですが、結局のところ、どのような関数を設定するかは人のサイトのほぼ丸写しでした。うーむ、敗北。

なお、参考ページを見ていただければおわかりのとおり、psychometric functionを書くためにはいくつかのやり方があります。たとえば、今回使ったようなprobit関数 (log(p/(1-p))によるのではなくて、gaussian分布の累積確率密度関数を使ってやるとか。というわけで細かく言うときりないようなのでこのあたりにて。

■ ω²

1-way ANOVAでのeffectの強さを示すindexとしてω²を計算してたんですが、値のrangeがなぜか0<ω²<1にならない。というわけで検証してみました。
ANOVAのテーブルを

--	SS	df	MS	F	P
effect	SSeffect	dfeffect	MSeffect	F	P
error	SSerror	dferror	MSerror	--	--
total	SStotal	dftotal	--	--	--

としたときに

ω² = ( SS_effect - df_effect * MS_error ) / ( SS_total + MS_error )

と計算されます。
よってこれの分母は正なので、分子を変形してみます。

SS_effect - df_effect * MS_error
= SS_effect - df_effect * MS_effect / MS_effect * MS_error
= SS_effect - SS_effect / F
= SS_effect * ( 1 - 1 / F )

というわけで、F>1のときだけω²は正であるようです。Web探してもどこにもそんなこと書いてなかったけど。
と書いてみてから、ω²==1になるのはSS_effect == SS_totalになるときだし、SS_effect == 0のときには絶対ω² < 0になる、と考えた方が早かったようです。やれやれ。

■ 時系列解析

時系列解析での時系列データ内に相関があるのかあたりまえで、そのような相関をどう取り除いていくかというのが時系列解析には必須です。ARとかARMAとかのモデルのようにある時間のデータY(t)がY(t-1)やY(t-2)などからどのように影響を受けているかを取り込んだものもあります。

■ 時系列データの解析でのMixed modelの使用

ガヤ、日記でのコメントありがとう。ほんとうにMANOVAでいいのかはよくわからないことだけ付け加えておきます。私が知っているかぎり、被験者をrandom effectにとって時系列の向きをfixed effectにとるmixed modelでやるべきと書いてある本もあります。

…多変量正規分布モデルでは、同一薬剤iを与えられた被験者の観測値は一定の正規分布N(μ_i,Ω)に従うものと見なされ、薬効は平均ベクトルμ_iを変化させるものと仮定されている。ところがこの種のデータでは、薬剤が平均ベクトルと同時に分散行列も変化させることが現実によく観察される。そのような状況では、次節の混合モデルの方が合理的である。「実験データの解析 分散分析を越えて」 広津千尋 共立出版 10章 p.311）

私自身はいまだにこのへん理解できてません。いや、fMRI関連で調べたりしたことはあるのですが。
追記：12:40 このことに関してSPSS ときど記(30)に有用な情報があります。

反復測定（測度）(repeated measures)の分散分析はこの２０年に何度も技術革新が起こった分野だ。
(1)ランダム効果（乱塊法）の一つの計画である，randomized block design，split-block design として捉えて分析する。これが古典的な反復測度の分散分析の仕方。
(2)自由度を調整して分析。
(3)MANOVAで分析。
(4)SASのproc mixed で分析する。
(5)自分でモデルを組みＳＥＭ（または共分散構造分析）で分析する。

つまり、私が書いていた自由度の調整->MANOVA->Mixed model、というのはまんま上の(2)->(3)->(4)だったのです。というかこのページ見るのは初めてじゃないんで、たぶん受け売りだったのでしょう。

■ Post-hocな解析

ガヤ、コメントサンクス。6/3の後半については直接ガヤに宛てたものではなかったのだけれど（今のところこの日記でですます調で書くと、誰かへのコメントへの返答のように見えてしまうようです）、コメントサンクス、アゲイン。
でもって、

gaya>> いわゆる世間一般でいう“多重比較問題”の意味（定義？）と照らし合わせて正しいんだろうか

これについてはもうちょっとポイントがわかるようなわからないようななので、わかったら教えてください。
以下のことをガヤが想定しているとは思いませんが、ついでに書いてみます。
いきなりデカめな話ですが。科学論文は、基本的には後付けでしか実験結果と解析を提出できません*1。だから恣意性や仮定が混ざる解析をできるだけ排除するように向かわなければなりません。この点でそもそも実験計画というものはデータが取れてからpost-hocにやるものではないので、その点で実験計画を使うのはおかしいというところはあります。ある種の大規模な調査（Fisherの農場での試験のような）のときにのみ受け入れられる性質を持っているとはいえます。ただ、さすがにそれは厳しすぎるので、実験結果が得られた後に恣意的な解析が出来るものは避ける、というのが現実的な手ではないかと思います。
たとえば、現状でも使用が受け入れられないものに、orthogonal contractがあります。例を挙げますと、control-condotion1-condition2という三つの因子があったときに、1-way ANOVAをやった後にpost-hocの多重比較をやらずに、[control] vs. [condition1 and contdition2]というふうな二つの項にsum of squareを分解して二つの項を比較する、というものです(三つの因子での多重比較が有意にならなくても、こっちは有意になる可能性があります)。このばあい、実験計画の段階で三つの項を上の二つの項に分けることが決まっていればよいわけですが、もしかしたら結果次第で[control and condition1] vs. [ contdition2]や[control and condition2] vs. [contdition1]に都合よく変えてしまうこともできるのです。我々は後付けでしか統計解析したものを論文として呈示できないですから、そのようなorthogonal contrastを実験結果が出てきてから論文に書いてもダメだと思うのです。
これが、後付けで都合のよいところだけ持ってくることが可能な解析の例です。ほかにもいくらでも挙げられますが、たとえば、動物ごとの結果がちゃんとconsistentであるかどうか示していない論文をJournal of Neurophysiologyから削ったら、どのくらい雑誌が薄くなることでしょう。
これらのことはつまり、論文を書く人は、自分に都合のよいことだけ書いて、都合の悪いことは書かない、ということになりがちであるという根本的な問題なのかもしれません。こういうところにだまされないように論文が読めるようにならなければならないし、その意味で本当に重要でかつ信ずるに足る結果を出している論文は私の分野では非常に少ないと思います（だから、fMRIのデータを集積してデータベースを作る、というような計画（先月のNature Neuroscience参照）については私はけっこう悲観的です。）。
それからもうひとつの大きな問題は、実験結果というものはnegativeな結果については論文にならないため、positiveな結果へのbiasが生まれるということです*2。つまり、一般的にはわれわれはα=0.05で統計をやっておりますが、ある同じことを検証するグループが20あったとします。じつはこのテーマは有意ではなかったのです。19個のグループではnegativeな結果が出ます。彼らは論文を書きません。残りのひとつのグループではpositiveな結果が出ます。α=0.05なのだから1/20でpseudopositiveが出るのもあたりまえです。そして彼らは論文を書きます。そうしてこの論文は他の論文に紛れ込んでしまいます。この問題はどっかで扱われているはずで、なんか名前がついているはずです。メタアナリシスや実験データの集積の問題とも関わっていることでしょう。
また、binごとの解析の多重比較問題というのは要するにこれです。そして、なんで対ごとの比較をせずに多重比較しなければならないかといえば、このようなα値の問題があるからです。というわけで、このようなα値の問題こそが多重比較問題だというのが私の理解です。多群の中から対の比較を持ってくるのもα値の問題であって、そのような多重比較の前にANOVAをやっておかなければならないことを考えると、time binごとの検定でも形式的には同様なはずで、、全体として有意であるという保証を持ってきてから行う必要があるようにも思えます。そもそもなんでbinごとの有意度検定がいけないか、それは100binでα=0.05で検定すれば5binが有意になるのはあたりまえだからでありますが、これはつまり実験結果としてあるbinで有意だったことを示すとき、それは単にほかの有意でなかったbinを無視している、ということであり、post-hocに有意なところだけ見つけてきてそこに注目して都合悪いところを無視する、という上記の問題でもあるということです。そこでどうすればよいか、それが私がこのあいだ提案したように、時系列データ全体を説明できるようなモデルを作ってやる、という方向へ行くべきなのではないか、というわけです。だんだん[そうであったほうがよいこと]と[これを間違えてはならないこと]との境界があいまいになってきている感じはするのだけれど。
長くなりました。元に戻ります。こうやって書いてみると、問題は[実験計画をあらかじめデザインする]ということと[GLMなどを使って実験結果をモデル化してやる]ということとの関係にあるようです。統計には実験計画的な側面とモデル化の側面とが混ざっています。例を挙げましょう。実験デザインの段階で因子と被験者を割り当てるrandomizationをするところは実験計画的な手法です。ここでは因子と被験者とのあいだにinteractionがないという仮定のもとでは効率的に因子の効果を見ることができるようにデザインされています。しかし実際にそのデータが出たときには、それをGLMなどでモデル化するのにその因子と被験者とのあいだのinteractionの項を入れてやって、それが有意でないことを確認する必要があるでしょう。しかししばしば前者の実験計画の段階の仮定を後者のモデル化のところにも適用してしまう、というわけです。
うーむ、こういうことはどこかで議論されているとは思うんだけど、そしてここで書いたことが正しいのかもよくわからないのだけれど、出してしまおう。

*1：論文を読んでると、introductionでこれこれこういう事を検証するために我々はこれこれの実験を行った、なんて書いてあるわけですが、著者はそれをすべての実験が終わってそれをまとめた後に論文を書き、上記の文を書くわけで、読者からはそのような研究動機が本当なのかを確かめることは出来ません。たまたま面白い結果が出たからって、たまたま面白い結果が出ました、なんて誰も書かないわけで、前からそのことを深く考えたかのような顔をして論文を書くわけです。これは良し悪しではなくて、もう、構造的に後付けが運命付けられているのです。
*2：Natureかなんかの記事でnegativeなresultをshareする、というような動きについて読んだことがあるけれど、それはこの問題と関係しています。

■ Surprise index

Poisson分布からのdeviationをbinごとに検定して出したP-valueを-log(P)に変換してsurprise indexという言い方で扱うというのはスパイクと行動の相関を見るのに使われるのを見ます。たとえばThompson and Schallの1990年代後半あたりの論文とか。Aertsenのunitary event analysisというのも同様なPoisson分布からのdeviationを見る分析を使っていたのではなかったっけか。
あ、ひさびさにガヤ日記 6/1へのコメントということで。
前にも書いたことだけれど、この種のbinごとの解析というやつに必ず付随するmultiple comparisonの問題というやつはどうしたらよいもんだろう。視覚刺激への反応潜時の決定にしても、σ=10msのkernelをかけてからspontaの2SDを越えたところ、というのがconventionalなやり方ではあるのだけれど、本当は問題があることは明白です。何よりこれらは時系列データであって、そういうものを解析するための統計を使う必要があります。たとえば、隣り合うbinとのあいだにはスパイク自体のあいだに相関があるのであって、行動との相関を見る前にこれらの影響を除去しなければなりません。
いちばん簡単な方法としては、repeated masure ANOVAになるでしょう。各binのスパイク数を従属変数として、bin [t1,t2,...ti,...tn]をひとつの因子、行動の方の条件、たとえば視覚刺激の種類をもうひとつの因子として、2-way ANOVAにすることでしょう。Mixed modelで、binと行動とのあいだにinteractionが出たら、そのsum of squareを分解してsimple main effectを検討することでとりあえずどのbinが有意であるかは言えることになります。Repeated masureにしておけば修正自由度εを使って検定してくれるでしょう。
もうひとつの解決法としては、MANOVAのような形になるのではないでしょうか。Binごとに解析せずに、従属変数を多変量にして、Y=[y1,y2,...,yi,...,yn]という各binのスパイク数を従属変数にして、これと行動の方の条件、たとえばrewardありなしやら行動の反応潜時などのregressor(X)を使ってモデル化(Y=Xβ)してやるわけです。こうすることによって、まずは全体としてのモデルがよくfitting出来ていることを示した後で、そのsum of squareを分解してゆく。球面性の仮定が成り立つかどうかで自由度の補正をすることで実質的な自由度もわかるようになります。
後者のようなことを実際にしているneuroscientistは見たことがないけれど、これがオーセンティックなだと思うのです。ところで前者と後者は等価なのだろうか。わからなくなってきました。
うーむ、ですます調だけでこういうこと書くのもむずかしいなあ（<-まだ試行錯誤中）。

■ 予測可能性

ガヤ日記3/30 「あまりに“昔”を参考しすぎると予測精度がひどく落ちる」おもしろい。どういうことだろう。統計的な性質を使ってるのではなくて、「「決定論的カオス」みたいなもの」でやってるからだろうな。
ところで前から思ってたんだけど、時間ドメインではなくて空間ドメインのほうはどうなんだろう。スライス上の細胞という限られたpopulationしか見ていないわけで、もしもっと多くのニューロンから（究極にはすべての脳細胞から）記録すれば予測可能性は上がるはず*1 だが、そうでないということだろうか。逆に、スライス上のデータの一部をランダムに取り除くとどのくらい予測可能性は落ちるか。Populationから一個のニューロンのデータを除いても予測はrobustなんだろうか*2、カオスってそういうの弱そうに思うのだけれど。そしてまたまたspontaとevokedとの問題。Spontaでは近くのニューロンの活動によって記述できるだろうが、evokedでは別の領野からの入力がcriticalに効いてくるであろう。そしてそもそもの予測可能性とcausal relationとの問題もあるしなあ。興味は尽きない。

*1：カオスだとどうなんだろう。統計的性質を使っているならば、どんなゴミの変数を加えても、データが有限回であるかぎりmultiple regressionのR²は上がってゆく。そこで変数を加える分ペナルティを与えたりする。そういえば有限回のデータからmutual informationを計算すると多めに計算されるバイアスがあるわけだが、このことと変数の数決定の話は等価なのだろうか。
*2：さっそくcross validationを思い出しつつ。

■ Binning

でもってbinningはまた一つのトピックでしょうな。そもそも脳がどう時間ドメインを情報の統合に使っているのか、ということから本当は捉えないといけないわけだけれど、前に書いたように現状はsigma=10msのカーネルで統合してるような扱いがされている。JPSTHが1ms binでスパイクが最大一個しか入らないようにする、とかいうのもどうも気持ち悪い。その意味で言及されていたJonathan Victorの仕事(metric-space analysis)はたぶん重要なんだと思う。いまだに理解できないんだけれど。ところでScienceでのモチーフが時間方向で伸び縮みしたりするのが時間ドメインの統合と関係してたりすると面白いかも（まだ読んでないんだけれどもしかして言及してる？）。

■ Journal of Neuroscience Methods

"The dynamics of spatial behavior: how can robust smoothing techniques help?"
Neri Kafkafi @ University of Maryland。
前報は
Journal of Neuroscience Methods '01 "Natural segmentation of the locomotor behavior of drug-induced rats in a photobeam cage."
ラットやマウスの足跡を記録して、その分布にsmoothingをかけていったいどこに片寄っているか、とかそういうことを研究するためのmethodology paper。カーネル密度推定とかではなくて、ノンパラでlocalにadaptiveな方法(LOWESS)を使用している。役に立つかも。
ところでspike列にガウシアンカーネルをかけてSDF (spike density function)を作るというのはようするに、一次元でのカーネル密度推定をやっているということであって、本当はスパイク列のISIの分散にもとづいて最も誤差推定が小さくなるようなカーネルを選ぶというのが筋だ。そこを経験的に最適化したのが論文でよくみるsigma=10msという値なのだと思う。
しかしたいがいはspikeのburstを見たいわけで、ISIはgaussianな分散をしているわけではないのだから、localにadaptiveにやるほうが本当はよいのだろう。とくにlatencyを見たいときとかは。Latencyの計算自体もいろいろポイントがありすぎるし、結局このへんをややこしくはせずに単にコントロール期間の2SDにするのが得策というわけだ。なこたぁわかってる(自分でツッこむと人がツッこめないのでヤメレ)。

■ 空間統計

的な解析が必要だったんで、Brian Ripleyが精力的に関与しているR言語について前からちょこちょこ調べているんだけれど、これはググりにくくて不便。しょうがないので"R language"とかで検索してる。新しく言語を作る人はネットで検索しやすいようなネーミングにすることを一つの条件にすると良いのではないだろうか。その意味でCとかC++とかは厳しいしが、PerlやSQLはよい。短くてしかも一般名詞と混同しないし(RubyやJavaは一般名詞が混ざってしまう)。いや、べつにNOT(-)で弾けばよいって？そりゃそうだけど。
と、きっと誰かがすでに言っているに違いないことをいまさらヌルく書いてみる。ていうかきっとどっかで読んだテキストの受け売りなんだろう。もうわかんないんだけれど。これがいわゆる「はてなの人は大昔に済んだ議論を蒸し返す」というやつなんだきっと(お疲れぎみ)。

■ JNS昨日の続き

Matlabコードは以下の通り。適当。Ver.6.5でモンテカルロの繰り返しは10万回でelapsed_time =128 sec。

n=100000; % no of iteration
T=20; % no of total trials
ch=2; % no of choices
MAXIMUMRUN=zeros(n,1);
for i=1:n,
  Q=[];for j=1:T,Q1=randperm(ch);Q(j)=Q1(1);end; % Q: question
  A=[];for j=1:T,A1=randperm(ch);A(j)=A1(1);end; % A: answer
  CRR=Q-A;CRRno=find(CRR==0); % correct answer when CRR==0
  % calculation of maxmum run of CRR==0
  maxrun=0;maxr=0;
  for k=1:length(CRRno)
    for m=1:length(CRRno)-k, if CRRno(k)+m==CRRno(k+m), maxr=m+1;end; end
    if maxrun < maxr,maxrun=maxr;end
  end
  MAXIMUMRUN(i)=maxrun;
end
[ [1:T]' hist(MAXIMUMRUN,1:T)'/n]

■ JNS

"Dynamic Analysis of Learning in Behavioral Experiments." Emery N. Brown @ MITか？

重要そうな論文なのだが、どこから取り掛かればよいかわからず止まっていたが、毎度お世話になっている http://www.hippocampus.jp/diary/2004_1.htm の1/14のところに簡潔なまとめがある。この辺のキーワードから攻めていけば良さそうだ。

あ、table 1はすぐ使えるか。二択のタスクで(chace rate=50%)、20trialのうちに8回連続の正解があったら5%有意でchance rateを超えていて、八択のタスクで(chace rate=12.5%)、20trialのうちに3回連続の正解があったら5%有意でchance rateを超えている、か。だいたい直感にあっている気がする。二択で五回ぐらい連続成功してもまだ偶然っぽい感じがするし。

ただ、このときの連続正解(run)は20trialのうちのどこであってもよいわけで、こういうときにmultiple comparisonの問題をちゃんと扱っているか検証しとかないといけない、と私はscan statisticsを使っていたときの経験からすると思う。

いや、モンテカルロやれば検証できるか、というわけでやってみた。20trialで二択をやったときのnull hypothesis(chance rate=50%)での20回のうちに出るsuccessのrunの最大値の分布を計算した。左がsuccessのrunの最大値。右が各runの確率密度分布。

    1.0000    0.0171
    2.0000    0.1949
    3.0000    0.3113
    4.0000    0.2259
    5.0000    0.1276
    6.0000    0.0647
    7.0000    0.0310
    8.0000    0.0148
    9.0000    0.0064
   10.0000    0.0033
   11.0000    0.0018
   12.0000    0.0006
   13.0000    0.0003
   14.0000    0.0001
   15.0000    0.0001
   16.0000    0.0000
   17.0000    0.0000
   18.0000         0
   19.0000         0
   20.0000         0

というわけで5%有意は8run以上だった。だいたい同じっぽい。八択のときを計算したら3run以上でP<5%になる。検算できてる。

お勧めエントリ

• 細胞外電極はなにを見ているか(1) 20080727 (2) リニューアル版 20081107
• 総説 長期記憶の脳内メカニズム 20100909
• 駒場講義2013 「意識の科学的研究 - 盲視を起点に」20130626
• 駒場講義2012レジメ 意識と注意の脳内メカニズム(1) 注意 20121010 (2) 意識 20121011
• 視覚、注意、言語で3*2の背側、腹側経路説 20140119
• 脳科学辞典の項目書いた 「盲視」 20130407
• 脳科学辞典の項目書いた 「気づき」 20130228
• 脳科学辞典の項目書いた 「サリエンシー」 20121224
• 脳科学辞典の項目書いた 「マイクロサッケード」 20121227
• 盲視でおこる「なにかあるかんじ」 20110126
• DKL色空間についてまとめ 20090113
• 科学基礎論学会 秋の研究例会 ワークショップ「意識の神経科学と神経現象学」レジメ 20131102
• ギャラガー＆ザハヴィ『現象学的な心』合評会レジメ 20130628
• Marrのrepresentationとprocessをベイトソン流に解釈する (1) 20100317 (2) 20100317
• 半側空間無視と同名半盲とは区別できるか？(1) 20080220 (2) 半側空間無視の原因部位は？ 20080221
• MarrのVisionの最初と最後だけを読む 20071213

月別過去ログ

[2024]

2|

1|

[2023]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2022]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2021]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2020]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2019]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2018]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2017]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2016]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2015]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2014]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2013]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2012]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2011]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2010]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2009]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2008]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2007]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2006]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2005]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2004]

12|

11|

10|

9|

8|

7|

6|

5|

4|

3|

2|

1|

[2003]

12|

11|

8|

7|

[2001]

10|

8|

6|

5|

4|

2|

[2000]

12|

9|

8|

7|

6|

3|

2|

1|

[1999]

9|

8|

7|