« 「意味なんてどこにも無いさ」 | 最新のページに戻る | Mutual informationとdecoding »
■ 比率のデータにエラーバーを付けたいんだけど
最高ですか! (<-奇をてらったごあいさつ)
どうもご無沙汰しております。ここに書いているということは暇だということを必ずしも意味しないけれど、ここに書いてないということはかならず忙しい。んで、しばらく頭の中をぐるぐる回っていたものがあったので、そのへんを吐きだしてすっきりさせて論文書きに集中したいと思いますので、いろんなところに不義理を働きつつもこんなもの書かせていただきます(超低姿勢)。
...なんて前口上をつけた原稿を作ってあったんだけど、なぜか久しぶりの三日連続投稿に。
んで、いきなり口調が変わるのですが、比率のデータにエラーバーを付けたくならないっすか?なんでもいいんだけど、たとえば二択の課題の成績が試行数120で正答数73で正答率61%だったとします。これは二項検定によって両側検定5%水準でchance level (50%)よりは有意に大きいです(図1の(1))。それを直感的に示すようなエラーバーをバーチャートに付けたい。これが今回の問題です。
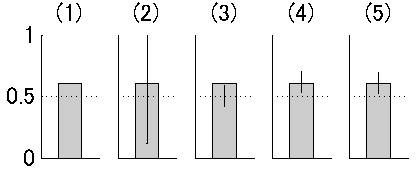
図1
普通は比率のデータにエラーバーなんて付けません。73/120という一つのデータだと思われているからでしょうね。でももしこれが正答数でなくて、反応潜時のデータかなんかだったらもちろんSDを付けることができます。同じように、73/120というデータのばらつき具合にエラーバーを付けてやりたいと思うのですよ。
まずは、間違った方法ではありますが、正答に1、誤答に0を割り振って、たんにそのSDを計算します。するとmean = 0.61, std = 0.49という値が出てきます(図1の(2))。もちろんこれは誤差の分布を正規分布と仮定しているのが間違いなわけです。(これをgeneralized linear modelでリンク関数をbinomialにして計算すれば間違いにはなりません。これは最尤推定でやっていることと同じのはずです。これについては後述。)
それでは今度は、比率の検定に基づいて考えてみましょう。ここでは二項検定で検定をしているわけですからそれを反映させましょう。つまり、試行数120で帰無仮説H_0:母比率p=0.50の場合の二項分布Bi(n,p) = Bi(120, 0.50)を計算します。Rだとこんなかんじ:
total <- 120 correct <- 73 x <- seq(0, total) bino_prob1 <- dbinom(x, total, 0.50) plot(x,bino_prob1)
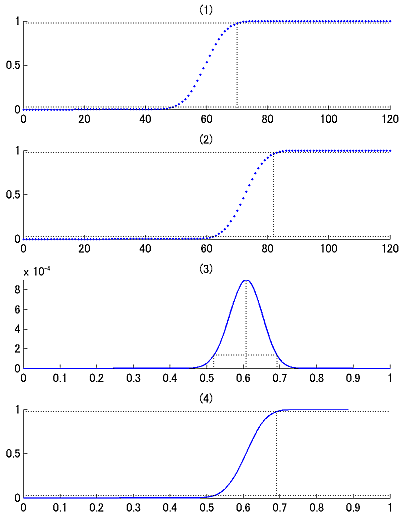
図2
両側検定5%有意水準で正答数70以上もしくは48以下だと有意です(図2の(1))。今回は73だから有意でした。この範囲を図に無理矢理入れるならこんな図(図1の(3))になりますが、こんなの誰も望んでない。だいたい試行数にしか依存してないし。
同じ発想で母比率が73/120だったときに実データがどのくらい散らばるかということを二項分布Bi(120, 73/120)
total <- 120 correct <- 73 x <- seq(0, total) bino_prob2 <- dbinom(x, total, correct/total) plot(x,bino_prob2)
で評価してやることも出来ます(図2の(2))。こうするとエラーバーの範囲は[0.5167 0.6833]となります(図1の(4))。これはもっともらしいですが、統計的な裏付けに欠けます。
さてこのへんからが本題です。Maximum likelihood estimationを考えてみましょう。データ73/120は既知で確率theta = 0-1のほうが変数で、尤度関数は
likelihood ∝ theta^correct * (1-theta)^(total-correct)
となります。
theta <- seq(0,1,1/total) likelihood <- theta^correct * (1-theta)^(total-correct) Lc <- likelihood / sum(likelihood) plot(theta,Lc)
このピーク値を見るとたしかに0.61になっていて、correct/totalがthetaの最尤推定値になっていることが確認できます(図2の(3))。またさらにこの尤度関数のcumulative density functionを作ってやると(図2の(4))、最尤推定値の95%信頼区間を[0.519 0.691]というふうに評価することが出来ます(図1の(5))。
この値は図1の(4)とほとんど変わりません。両者の違いは、二項分布では横軸xがデータの個数で離散的になっているのに対して、最尤推定では横軸thetaが連続値になっているという点ですが、thetaのほうを離散的にして計算すると(theta = [0:1/120:1]としてやる)微妙に違う値になります(図3の上 緑が二項分布、青が尤度関数、図3の下 緑が尤度関数-二項分布の引き算)。数学的にはべつものなんでしょう。つまり、二項分布Bi(n,r,p)のグラフを縦に見るか横に見るか、という話になります。くわしくは「ベイズ統計学は本当に有効か?」赤嶺達郎および「枠どり法とPetersen 法の区間推定における伝統的統計学とベイズ統計学との比較」 赤嶺達郎(pdf)(今回の話のネタ元のひとつ)を参照、ということで。
Webを探したら「検定と区間推定」奥村晴彦(TeX本で有名な方)にRでのimplemantationがありました。なんかこれを読むといま書いたことのすべてが書かれているような気がしますが、まあこうやって書いてみることは悪くないことで。
> binom.test(73,120,0.5)
Exact binomial test
data: 73 and 120
number of successes = 73, number of trials = 120, p-value = 0.02208
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.5150437 0.6961433
sample estimates:
probability of success
0.6083333
ともあれ最尤推定まで考えると、それなりに意味のあるエラーバーが書けそうです。役に立つと思うんですけど、なんでみんな使わないんですかね。
さて、こんなことを計算している目的の一つはベイズ統計のお稽古だったわけで、「ベイズ統計学入門」渡部洋著を元にしてさらに先に進みます。
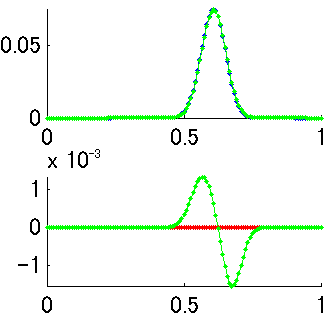
図3
Maximum likelihood estimationで得た最尤推定値はベイズ統計の立場から見れば、無情報のprior (p(theta)が一定)を用いたときのMAP推定値と等価です。つまり、さっきの尤度関数(図2の(3))はposteriorの分布と捉えることが出来て、点推定をするとピーク値の0.61を取ることになり、区間推定をするなら図2の(4)のように信頼区間を計算することが出来ます。
ベイズ統計の場合には、信頼区間(confidence interval)ではなくて、信用区間(credible interval)として、全体の10%の面積が除外されるような縦軸の値を設定して計算します(図2の(3))。これはMAP推定自体がピーク値(mode)を使っていて、median (=50% percentile)ではないということからすれば納得がいきます。こうして計算された信用区間は[0.520 0.692]となります。これはさっきの信頼区間の値[0.519 0.691]とほとんど変わりません。分布が歪んでないのでそりゃそうでしょうね。
教科書まる写し口調ですが、今まで扱ってきた二項分布をBi(total, correct/total)と表現しておくと、この尤度関数L(=ベイズ統計でのposterior)はベータ分布Be(correct+1, total-correct+1)と表現できます。二項分布のベイズ推測での自然共役事前分布がベータ分布であることがわかっています。つまり、priorがベータ分布なら、posterior ∝ likelihood * priorもベータ分布ということ。
無情報のpriorを使う場合にはこれはBe(1,1)と書けて、これはpriorではtotal=0, correct=0となっていることと等価です。このときのposteriorは
posterior ∝ likelihood * prior = Be(correct+1, total-correct+1) * Be(1,1) = Be(correct+1, total-correct+1)
となるわけです。確認のためこのベータ分布をplotしてみますと、これまでの尤度関数とまったく一致します(図3の上 赤がベータ分布だが青に重なって見えない 図3の下 赤が尤度関数-ベータ分布の引き算)。
面白いのは、ベイズ推定の式がたんにベータ分布の中身Be(a, b)の足し算になっている点ですね。もしここでpriorとして無情報のprior(Be(1,1): total=0, correct=0)を使わずに、局所一様分布のpriorというやつを使うとBe(1/2, 1/2)となります。これはtotal=-1, correct=-1/2としているのと同じということで、これは得られたデータから1 trial分差っ引いてposteriorを作っているということになります。おお! ここでも出てきた補正の思想!
というわけでpriorとしてはBe(1,1)とかBe(1/2,1/2)とかがありうるのだけれど、はっきり言ってこのような単純な状況ではベイズ統計が出てくる必要性はあまりないと言えましょう。ではどういうときに必要かというと、複数のセッションを足し合わせるような状況ですね。(このへんから北大の久保拓弥先生のweb資料(pdf)に依拠しながら進みます。)
これまで使ってきた73/120というデータですが、じつはこれが5回分のセッションの集計だったとします。たとえば、{16/30, 24/30, 12/20, 11/20, 10/20}というデータだったとします。この5点をプロットしてそれのSDでエラーバーを付ける、というやりかたがありますが、これは試行数の120を使ってないので正当な評価とは言えないでしょう。(セッションごとのばらつきを評価しているというのはわかるのだけれど、それが0.5からdeviateしているかどうかを検定するとしたらそれは意味がない。)
データのモデル化を考えてみると、各セッションごとに二項分布Bi(n, 73/120)から出てきたと考えるとします。これはセッションごとにthetaが一定(=73/120)であるとするモデルですが、二択の心理実験とかではだいたい当てはまらないわけです(これはoverdispersionが起こっているかどうかで検証できる)。そこでセッションごとのthetaが73/120からばらつく(とりあえず正規分布でSD=0.1として生成してやると{0.52 0.80 0.60 0.55 0.51, ....}となる)というふうにするのがrandom effectモデルで、このSDを決めてやるために経験ベイズ、階層ベイズが出てきて、そうするとセッションごとのばらつきとセッション全部のばらつきとを評価することが出来て、エラーバーとしてもそれを示すのが正しいのだと思うのだけれど、おっとここで時間のようです(<-逃げた)。
いったん逃げたけど帰ってきた。やりかけなんだけどRでの解析を書いておくと、まずデータ作り:
id <- factor(c(rep(1,30), rep(2,30), rep(3,20), rep(4,20), rep(5,20))) y <- c(rep(1,16), rep(0,14), rep(1,24), rep(0,6), rep(1,12), rep(0,8), rep(1,11), rep(0,9), rep(1,10), rep(0,10)) data3 <- data.frame(y=y, id=id)
これをidを無視してセッションをまとめたときの解析は、generalized linear modelでリンク関数をbinomialにしたもので、こんなかんじ:
result1 <- glm(y ~ 1, family = binomial, data = data3) summary(result1)
結果は
> summary(result1)
Call:
glm(formula = y ~ 1, family = binomial, data = data3)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.369 -1.369 0.997 0.997 0.997
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.4403 0.1870 2.354 0.0186 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 160.68 on 119 degrees of freedom
Residual deviance: 160.68 on 119 degrees of freedom
AIC: 162.68
Number of Fisher Scoring iterations: 4
となっていて、Interceptのestimateは0.4403で、standard errorは0.1870。だから比率の最尤推定値および95%信頼区間は
> 1 / (1 + exp(-0.4403)) [1] 0.6083305 > 1 / (1 + exp(-0.4403+0.1870*1.96)) [1] 0.5184366 > 1 / (1 + exp(-0.4403-0.1870*1.96)) [1] 0.6914315
というふうに正しく計算できます。
また、セッションごとにIDが付いたデータの場合はGLMM(混合モデル)を使って、さっきのdata3を解析すると、
library(glmmML) result3 <- glmmML(y ~ 1, family = binomial, cluster = id, data = data3) summary(result3)
というので計算が出来ます。この結果は
> summary(result3)
Call: glmmML(formula = y ~ 1, family = binomial, data = data3, cluster = id)
coef se(coef) z Pr(>|z|)
(Intercept) 0.4337 0.2269 1.912 0.0559
Scale parameter in mixing distribution: 0.2777 gaussian
Std. Error: 0.2753
Residual deviance: 160.2 on 118 degrees of freedom AIC: 164.2
となって、idのrandom effectのSEが0.2753と出てきます。このため、interceptの推定もglmから多少ずれるので、比率の推定も以下のように多少低めに出ていて、信頼区間も広くなっています。ひとつ突出している24/30が効いている分を考慮しているかんじがうかがえます。
> 1 / (1 + exp(-0.4337)) [1] 0.6067568 > 1 / (1 + exp(-0.4337+0.2269*1.96)) [1] 0.497244 > 1 / (1 + exp(-0.4337-0.2269*1.96)) [1] 0.7064955
ただ、glmmMLの結果の見方がまだよくわかってないので("Scale parameter in mixing distribution: 0.2777 gaussian" ってなんでしょう。以前の資料を見るとここはSDが表示されていたんですけど。)、このへんで止まってます。
Chance levelから有意かどうか、というのはgeneralized linear modelまで来ると、H_0のrejectという形ではなくてモデル選択ということになるので、inteceptが0 (比率が0.50)のモデルと最尤推定で得られたinterceptでのモデルとでAICを比較するということになるんでしょう。論文書きのときはpが付けられないと困っちゃうんだけど。
さてさて、ここからが本番です(本気)。長々と引っ張ってきましたが、このエントリの最終目的はじつはmutual informationのバイアス問題に関連しているのでした。有限の試行のデータから刺激sと応答rとの間からmutual informationを計算するときに必要なのはp*log2(p)の計算なわけですが(応答rがK binあるうちのi binに落ちたときの確率をpとする)、このpの最尤推定値として、あるbinに落ちたspike数yとその総数nを実測データから計算してつくったy/nを用いているわけです。このことはエントロピー推定のバイアスを生むわけですが、そもそもcountデータからの比率の推定に基づいているのだから、今回扱ったような手法でエントロピーおよびmutual informationでもベイズ推定と信頼区間を計算してやることが可能となります。
基本に戻ると、刺激sと応答rとのあいだのmutual information MI(s,r)は二つのエントロピーの引き算:MI(s,r) = H(r) - H(r|s)で計算できます(direct method)。それぞれのエントロピーはresponse entropy: H(r) = Σp(r)*log2(p(r))、noise entropy H(r|s) = ΣΣp(s)*p(r|s)*log2(p(r|s))として計算されます。
ここで比率のベイズ推定のエントリの応用問題ですが、応答rはK binあるので多項分布です。多項分布の自然共役分布はDirichlet分布となりますので、これをpriorとおいてベイズ推定をします。あるk binでのスパイク生成率の最尤推定値がy_k/n (実データでnスパイクのうちy_kスパイクがk binに落ちた場合)だったとすると、priorをa_k/A (k binのcountをa_kとして、A = Σa_k)とおくと、あるk binでのスパイク生成率のMAP推定値は(y_k + a_k)/(n + A)となります。でもってnoninformative priorだとa_k = A/K (K=bin数)となるというわけです。(このへんはHausser and Strimmer "Entropy inference and the James-Stein estimator, with application to nonlinear gene association networks"(pdf) の説明を使いました。)
というわけでこれも手計算してみようかと思いましたが、bin数Kが大きいとあっという間に次元が増えてたいへんなので止めとしておきます。ともあれ、mutual informationでもベイズ推定して信頼区間を付けられるというわけです。今日はこんなところまで。あしたにつづきます。
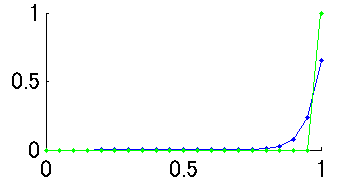
図4
追記:コイダーマンさんからコメントいただきました。どうもありがとうございます。なるほど、図3での緑(二項分布)と青(尤度関数)の違いはcorrect=20; total=20の場合を考えるとより明確になりますね。さっそく図を作ってみました(図4)。二項分布だとcorrect ratio 100%しかありえなくなってしまうけど、尤度関数だとcorrect ratio 90-95%あたりの可能性もそれなりにあるということがこの図だとよくわかります。
# コイダーマン
こんちは。
私も行動実験や心理実験をやってて同じことを悩んでましたヨ!
自分が読めるようなわかりやすい本には図1(4)の説明しか載ってなくて、
でもその方法だと、たとえば正解率が100%(20回中20回とか)のときに
信頼区間がゼロになっちゃうんですよね。
でも、そんなわけない!
真の確率は98%なんだけど、たまたま結果が100%になったってことだって起きるはずだ!
当時は尤度の読み方どころか文字すらも知らなかったので
自分で一から考えて答えにたどり着いたときは感動したです・・車輪の再発明と言うんでしょうか。
適当に二項分布の母確率pを仮定して、
そのときに実験データ(たとえば20回中20回)が生じる確率を求める。
図の横軸を仮定した母確率のpにとって、縦軸を実験データの発生確率でグラフを書くと・・
母確率pは0~1まで均等にあると仮定して、そのpが選ばれるのをΔpと考えると
・・あ、信頼区間が計算できちゃった。やった!って。
Mutual Infomationの信頼区間計算ってのはいいですね!
これまで私はあまり考えずにブートストラップのような方法で求めましたです。
平均発火頻度をポワソン分布でフィッティングして、
試行回数分のデータを擬似発生させて、自分がきめたBINで相互情報量を計算。
これを1000回とか繰り返したら相互情報量のばらつきがわかるかも、とか。
でもこれじゃ
ある刺激への応答が全部0spk/sだったときに信頼区間がゼロになって困る。
繰り替えしが5回とか少なかったりすると、真の平均発火頻度が0以上である可能性は相当高いのに。
続編期待してます。
# コイダーマンあ・・書き込みした後に思い出した・・
# pooneil二項分布の信頼区間を求めようとしたのは、実験の解析が目的じゃなかった!。ゲームRagnarokOnlineで錬成だったか何かの成功確率が、いくつかの条件間で差があるのかないのかを匿名某で議論してたときのことだったワ!
心理実験やってたから、なんてウソウソでした!
コイダーマン、どうもありがとうございます。(言いにくいのでさん付け省略で。)
なるほど、20/20の例を使えば、図3上の二つのプロットの違いがより明確に示せますね。追記しておきます。
>RagnarokOnlineで
それ正直に申告しなくてもいいよ!!!
つーかそれアカデミックな議論ですね。
わたしも某巨大掲示板で複数のランキングの相関係数を計算して議論したことがあるけど。