pooneilの脳科学論文コメント

■ モンテカルロ(1)

昨年くらいに途中まで作って放置してあったエントリを貼っておきます。しかも「間違ってる！」なんてメモまで付いてる。なんだったか忘れたので埋め草用に。しかも明日に続きます。

---

モンテカルロでなんかの値のmeanとsdとを計算するために10万回とかループを回して、全部の値を行列に収納してからそれのmeanとsdとを計算していたのですが、それではおっつかなくなってきたので、ループごとにmeanとsdとをアップデートしてゆくような漸化式の形を作るようにしました。そんなことすらサボってたわけです。

平均：MEAN; 変動(sum of square)：SS; 標準偏差：SD; として、
MEANn = (MEANn-1 * (n-1) + newdata )/ n
SSn = SSn-1 + (n-1) * (MEANn-12) - n * (MEANn2) + newdata2
SDn = sqrt(SSn / (n-1) )

たとえば、randnでmean=0、sd=1の正規分布の乱数を生成させるのを10^8回繰り返してその乱数のmeanとsdを計算してやると、

tic;
nummat=10.^(1:8);data=[];loop=10^8;
n=randn(1,1);meanN=n;meanNp=n;ssN=0;ssNp=0;stdN=0;
for i=2:loop
	n=randn(1,1);
	meanN = (meanNp*(i-1)+n)/i;
	ssN = ssNp + (i-1)*(meanNp^2) -i*(meanN^2) + n^2;
	stdN = sqrt(ssN/(i-1));
	meanNp=meanN;ssNp=ssN;
	if ~isempty(find(nummat==i))
		data=[data;i meanN stdN];
	end
end
toc;

figure
hold on
plot(log10(data(:,1)),data(:,2),'ro')
plot(log10(data(:,1)),data(:,3),'bo')

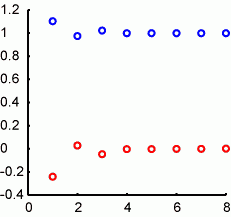
わたしのノートPCではelapsed_time =18975secで計算されます。図の通り、横軸がループの回数(log10(x))。縦軸がそれぞれのループの回数で計算された値で、赤が乱数のmeanで、回数が増えるほどに0に近づきます。青が乱数のsdで、回数が増えるほどに1に近づきます。10^5=10万回くらいやればだいたいよさそうなことがわかります。

ほんとうはもっと良いのは、matlabが得意とする行列での演算と組み合わせることで、

std(randn(10^4,10^3));
elapsed_time =	2.0160

なんてので10^4個の乱数のsdが10^3個計算できるので、それを前述の漸化式のように組み合わせたほうが10^7個の乱数のsdを計算するのはもっと速くなることでしょう。ちなみに直で計算させると

std(randn(10^7,1));
elapsed_time =  165.8200

メモリーが圧迫されるのでけっこう時間がかかってしまいます。さらに、うちのノートPCではもう一桁増やすと

std(randn(10^8,1));
??? エラー: ==> randn
メモリが足りません.HELP MEMORYとタイプしてオプションを確認してください

なんて出てきて、もう計算できません。