pooneilの脳科学論文コメント

■ 信号検出理論の感度(d-prime)にエラーバーを付けたい！(解決編)

以前 「SDTのd'にエラーバーつけたい。」ってのを書いたことがあるけど、このときの図の軸をpではなくてnorminv(p)にしてしまえばd'が等しいところが並ぶのでCDFの計算が簡単になる。

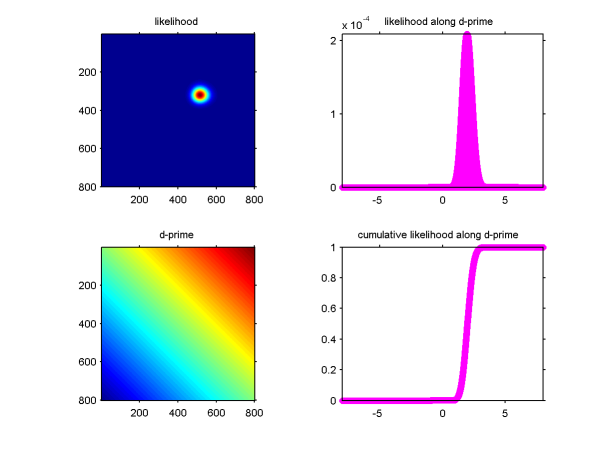
これでconfidence intervalも計算できるんで、解決って思ってたんだけど、元のp(hit), p(fa)での軸も悪くないんではないかということに思い当たった。というのも、大して大きいデータではないので、N=hit+miss, M=fa+crを固定した上で、p(hit), p(fa)をそれぞれ0-1までふって尤度を計算してやれば、たかだかM*N個の尤度の計算で済む上に、もっとも重要なことは、p=0,1での尤度の計算も出来る。

norminvだとここはInf, -Infに発散してしまうのでd'が計算できないわけだけど、それはそれとしてそのデータ点の尤度が計算できるならば、たとえd'がInf, -Infになってしまっても、尤度関数の期待値から、ベイズ推定的にd'の推定値と信頼区間を計算できる。つまり、hit rateが 30/30だったとしても、d'が推定できる。これはよいんではないだろうか。

考え方としては、二項分布で20/20のときの信頼区間計算する話と同じ。

いや、d'そのものは推定できないけど、そのupperboundかloweboundが計算できる。たぶん、hit = 30/30のときに便宜的に29/30だったらd'いくつになるか計算するのと同じことを、もうちょっとまともにやったことになるのではないだろうか。

ここまで考えると、もうちょい逸脱して、d'自体の絶対値にこだわらずに、M*N個の可能なd'のランクに変換して、ノンパラメトリックd'みたいなものを定義してしまえばよい。 探せばこういうのありそうだ。

最尤法で尤度がmaxのところを推定値とするのはMAP推定と等価だけど、maxではなくて分布の重み付け平均を推定値として取るのはなんと呼べばよいのだろう。「ベイズ推定」と呼ぶのはへんな気はするが、noninformative priorでのベイズ推定と言えばウソはついていないのか。

ためしに計算してみた。p(hit) = 30/30で、p(FA) = 10/20の場合。

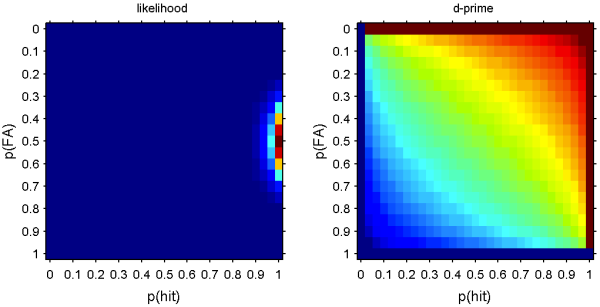
でもって、ここまできたらたぶん、dprime = norminv(p(hit)) -norminv(p(fa)) の式を使うのがアホなんだろうな。ノンパラにするのも極端な話で、二項分布かなんかを持ってきて、ノイズのシグナルの二つの分布の離れ具合はKL距離で評価とかそんなかんじか。

---

超分かった！d-primeのドメインではなくて、[p(hit), p(fa)] 自体のベイズ推定を行えばいいんだ。p(hit)=1だったとしても、30/30と3000/3000とでは推定されるpは違うし、それはけっして1ではない。それを使ってd-primeを計算してやればよい。しかもこれはけっこう実用的だ。

matlab関数作ってみた。たとえば[hit miss fa cr] = [10 0 5 5]の場合、p(hit)=1からはd'=Infになってしまうが、尤度からのp(hit)の推定値は0.95となる。これから計算したd'は1.69となる。妥当なかんじ。

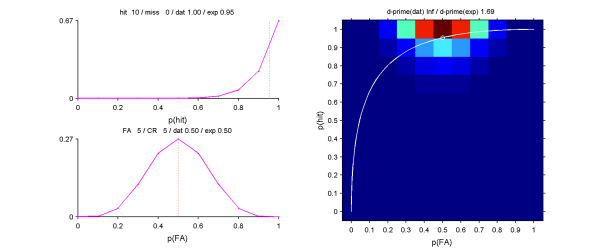
[hit miss fa cr] = [30 0 15 15]の場合、尤度からのp(hit)の推定値は0.98となる。これから計算したd'は2.10となる。

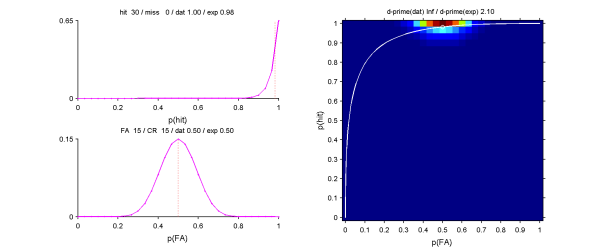
[hit miss fa cr] = [100 0 50 50]の場合、尤度からのp(hit)の推定値は0.99となる。これから計算したd'は2.53となる。だいたい満足した。

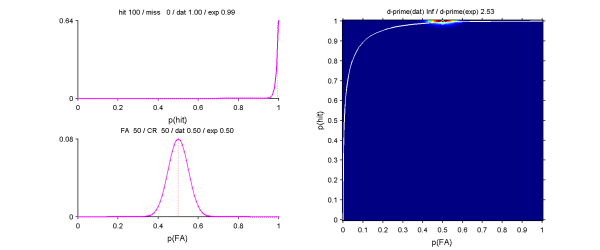
[100 0 0 100]とか極端な状態でd-prime(exp) = 5で、実際にはお手つきがあるから[99 1 1 99]でd-prime(exp) = 4。妥当なかんじ。ふつうのd'では>3とかに意味がないって言われるわけだけど、よっぽどそんなにでかいところまで発散しない。

matlabコードは http://pooneil.sakura.ne.jp/dprime_lik.m にアップしておきました。無保証でどうぞ。なんか間違いがあるようならぜひ教えてください。