« 速報 | 最新のページに戻る | Nature 7/1 »
■ Science Newsome論文つづき
"Matching Behavior and the Representation of Value in the Parietal Cortex." Leo P. Sugrue, Greg S. Corrado, William T. Newsome
mmrlさんから6/29のコメントにあるbayesian harvestingに関する詳しい解説と図が届きました。どうもありがとうございます。以下に掲載します。今日はmmrlさんによるゲストブログみたいなもんですので、<blockquote>に入れないで地の文に入れます。貼り付けてある図は図2の方です。図1は6/30のところに貼ってあります。はてなは一日一枚しか画像が貼れないもんで。なぜか図が小さくなってしまったので6/29にもっと大きい図2を貼っておきました。そちらをご参照ください。 (追記:はてなからの移行の際に図の配置を直しました。図1、図2ともに下に貼りました。)
mmrlです
先日説明したbayesian harvestingですが、図をはさんでいただけるということですので、ちょっと計算をしてみました。Corrado のポスターの式を参考にしました。すでにpooneilさんがやさしい言葉で説明されているVI-VIの場合に最適行動はmatching にほぼ等しくなることを式で書いただけというだけです。少々長くなりますが、私のような式や実際に動くプログラムやロボットで納得する人間のエゴとお許しください。
離散時間で進行するVI-VI平行スケジュールはある確率で報酬が出現し、取るまでそのままという形で実現できます。毎回red/greenに報酬が出現する確率をp_red/p_green とすると、greenに報酬が存在する確率P(r_green)は前回greenをためした回からの回数をkとしてP(r_green)_k = 1-(1-p_green)^k となります.
なぜなら,
1回では
p_green,
2回では最初の1回で出現する確率+1回目で出現せず2回目で出現する確率=
p_green + p_green(1-p_green),
3回目では
p_green + p_green(1-p_green) + p_green(1-p_green)^2
となり
k回目では
p_green (1 + (1-p_green) + (1-p_green)^2 + ... + (1-p_green)^(k-1))
となり等比級数公式から
P(r_green)_k = p_green(1-(1-p_green)^k)/(1-(1-p_green)) = 1-(1-p_green)^k
red を選び続ければ、p_greenがどんなに小さくてもP(r_green)_kは1に漸近しますから、
ほぼ100%でgreenに報酬があることになります。
ここで、baysian harvestingとは、報酬の存在確率を初回をP(r_red) = 0 , P(r_green) = 0 として上の式にしたがって計算し、その回(t)におけるP(r_red)(t) > P(r_green)(t)ならredを逆ならgreenを選ぶ最適選択者とします。とすると図1にあるようにredが上回ればredを選択し、確率0にリセット、green が上回れば..という周期パターンで行動を選択することになります。
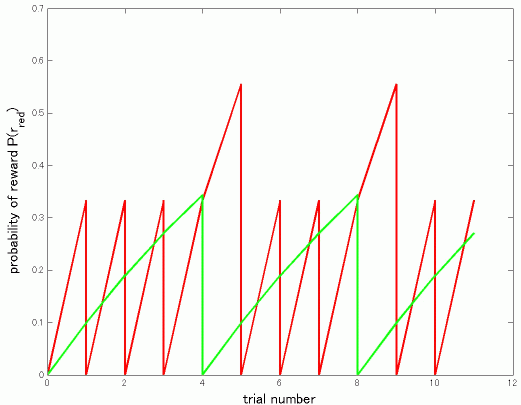
figure 1
ここで、p_red > p_green の場合に限定して考えると、redを選ぶ回数n_red(>=1)回に1回green を選ぶパターンになるはずです。(図1では3回に1回p_red = 1/3, p_green = 1/10)
したがって選択の割合はn_red:1となり、このときn_redは log(1-p_red)/log(1-p_green) の小数点きりすて整数になります。
なぜなら,n_red回はredを選ぶので報酬存在確率は
p_red > 1-(1-p_green)^n_red
次の回でこの関係が逆転するので、
p_red < 1-(1-p_green)^(n_red+1)
これを変形して (1-p_green)^(n_red+1) < (1-p_red)
の両辺をlog取って変形すると
n_red > log(1-p_red)/log(1-p_green) -1
となる最小整数がn_redであるから、
n_red = floor[log(1-p_red)/log(1-p_green) ]
ここでfloor[x]はx以下の最大整数
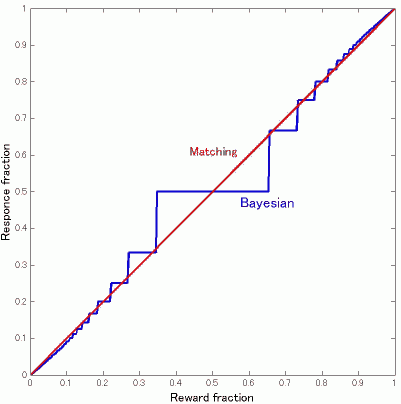
figure 2
これで得られるn_redを使って選択割合、n_red/(1+n_red)を報酬割合p_red/(p_green + p_red)の関数としてプロットすると図2のようになります。(p_red + p_green = 1/3の制約を与えています)。matching は、選択割合と報酬割合が一致するのですから傾き1の直線になります。ごらんのような階段関数となりますが、n_redが増えるにしたがって接近しているのがお分かりいただけるかと思います。ただこれが完全に一致するかというとどうかわからないところです。細かいところまでみると、どうも完全に一致しないように思います。
mmrlさん、どうもありがとうございました。すごい。
ひとつコメントですが、図2ってスムージングをかけてやると、逆S字型のカーブになりますが、それってgeneralized matching lawでいうところの過小な適応(強化の比率ほどには選択の比率が0.5からズレない)の形に近似できる感じがします(スムージングをしてから両座標をlogスケールにすると傾きが<1になる)。Bayesian harvestingによってやや過小ぎみな適応をしている、ということになるとじつはこっちの方がFig.1にある青線と黒線のずれをよく説明できるような気もしてきます。(あ、過小じゃなくて過大だったかも。)
そういえばVI-VI並列強化スケジュールとVR-VR並列強化スケジュールに関しては"高橋雅治(1997) 選択行動の研究における最近の展開:比較意思決定研究にむけて"に記載がありました。VI-VR並列ではVIのほうがより多く選択されることや遅延低減仮説に関して書かれています。やっぱりこのへんまだいろいろありそうです。
- / ツイートする
- / 投稿日: 2004年07月01日
- / カテゴリー: [価値による行動選択 (expected value)]
- / Edit(管理者用)
# mmrl
すみません、いきなり間違い発見しました。1つめの囲み記事の最終行は「ほぼ100%でgreenを選択するようになります。」です
# mmrlもとい「ほぼ100%でgreenに報酬があることになります。」
# pooneilありがとうございます。直しておきました。
# mmmmmmrlさん、大変分かりやすい図とご説明、ありがごうございました。非常によく解りました。さて、mmrlさんの図との対応を考えるにあたって、実際に何トライアルくらいに1回、報酬を貰っていたかが気になってきました。議論を単純化するため、overall maximum reward rate (0.15 rwd/sec)を採用しましょう。また常にtargetが表示され続けていたと仮定して考えると、1トライアルに要する時間は平均1950ms + rewarding timeとなるでしょうから、大体2秒と考えてよさそうに思います。0.15 rwd/sec = 1 rwd/6.66 secですから、平均3−4トライアルに1回の報酬があったと考えられます。これはgreenとredの両方を加算した条件ですから、p_red:p_green = 1:1の場合を考えると、red choiceに報酬が与えられたのはそのうちの半分ですから、6−8(平均約7(本当は6.6))トライアルに1回ということになり、red choiceによるreward rate、p(r_red)は単純計算で1/7 = 0.14となります。ここでmmrlさんの図2を見てみると、MatchingとBayesianとの間の一致はかなりよいレベルです。以下同様にp_red:p_green = 3:1の場合p(r_red) = 3/14 = 0.21p_red:p_green = 6:1の場合p(r_red) = 6/24.5 = 0.24p_red:p_green = 8:1の場合p(r_red) = 8/31.5 = 0.25となります(あくまで概算)。p(r_red) = 0.25でもMatchingとBayesianとの間の一致はかなりよいです。ということは必ずしもMatchingである必要はなくて、Bayesianでも説明可能なのではないかということになりそうに思えます。つまり、そろそろ別のターゲットに報酬がつきそうだということをベイズ的な計算に基づいて予想して、選択するターゲットを切り替えているのではないか、というように思えます。このことは、reward rateの小さい方のターゲットを選択する間隔がどれだけ周期的になっているか、また、その選択の切り替えが、mmrlさんの図1で予想されるタイミングにどれだけ一致しているかを検討することで見えてくるのではないでしょうか。ただ、pooneilさんの調査によると、CODを用いているとのことなので、この影響をどう考慮するかも考えなければなりませんね。
# pooneil直しておきました。
# mmmmん?↑の私のコメントでは、p_red + p_green = 1の制約が度外視されているような……。
# mmrlたしかに、bayesian でもよい予測はでき、行動が周期的かどうかを議論することで違いは出せると思いますが、bayesian は細かい短期記憶を必要とする(Matchingに比べて)複雑なモデルなので、オッカムのかみそりを使うと簡単なモデルで説明つくならそっちでいいじゃないかということになる。もし周期性が本当に観察されるなら、bayesianが本当っぽいということになるのかもしれませんが、それはでそうにないのではないかと考えます。なぜなら、bayesian では完全に行動ごとの報酬出現確率を既知として計算されている。本来は確率はサルにはわからないわけで、これを学習する必要があるはずです。しかも報酬出現確率は突然変化するために、常に学習しようとすることが報酬の最大化につながるはずです。とすると各試行におけるサルの行動は完全にはbayesianで予測できるとはおもえない。やるならば、長い時間スケールでは報酬出現確率を学習し、短い時間スケールでは報酬存在確率を考慮しながら行動をするのが最適になるのではないかと考えています。じつはこれはSugrue et al のsupporting online material のfigure S1 choice trigger averaging (CTA) of rewardと関係があって、彼らはこれはうまくexponential curveで近似できているといっていますが、私はこの曲線は異常に3-5trial 前までが大きくなってうまくフィットしない様に感じるのです。これは上に説明したような2重のタイムスケールを持つ学習/決定モデルでフィットできないかと考えています。モデルに関してはまた後日考えて見たいと思います。それと私のミスで、図2の制約条件はp_red + p_green = 1/3です。ごめんなさい。pooneilさん何度も申し訳ないです。overall maximum reward rate (0.15 rwd/sec)で1試行で約2secですから、報酬率は約0.3ということで、大体あっているはずと思って1/3にしました。たしかSugrueのポスターにも約1/3という記述があったように記憶しています。
# mmrlpooneilさんコメントありがとうございますスムージングを掛けてlogとってみるとどうなるか?って話ですが、実は図2の階段関数は、実はめんどくさくて数値解しか出していないので、解析解をみてみないと厳密にはなんともいえないです。ただこのカーブはp_red + p_greenの値に依存して変化します。1/3のときはよくあっているように見えますが、1にするとS字カーブになることを確認しています。
# mmmmああ、そうか。単純に1/3を1:1, 3:1, 6:1, 8:1に分けるだけでよくて、実際の実験状況でのp(r_red)はminimumが1/3 * 1/2 = 0.167、maximumが1/3 * 8/9 = 0.296となると見るだけで良かったのか。先のはダサダサしたね(笑)。
# mmmm報酬出現確率が本当にサルにとって未知であるかどうかは検討する必要があるのではないでしょうか。長期のトレーニングによってサルは、トータルの報酬出現頻度が約1/3であり、しかも報酬のred/green (or green/red)の比率が、1/1, 3/1, 6/1, 8/1しかないことをサルはすでに学習済みである可能性があると思います。するとブロック毎に学習すべきは、どの比率であるかの選択だけでよいことになります。そして各ブロックは100-200 trialsを含んでいますから、そのほとんどを既知の確率に基づいて行動していることはありそうなことではないでしょうか。
# mmrlもしかしたら、mmrlさんの考えと基本的には同一なのかもしれません。モデルの方も期待しています。
なるほどそうか、長い訓練でいくつかの確率のパターンをいくつかあらかじめ知っていてそれを選択するということも考えられますね。考えていませんでした。わたしが考えていたのは単純にbayesianで予測される報酬の確率と実際の報酬との誤差が確率をupdateさせるモデルです。mmmmさんの言われる方法でも別にモデルができますね。ただ、いくつかのモデルを当てはめることができても、これをどうやって比較したらいいんだろう...。自分でVI-VIの行動データを取ろうかな? もう少しつめる必要がありそうです。
# mmrlbayesian harvesting にchange over delay を入れてみた場合も、一応計算してみました。結果はあんまりかわらなくてがっくししたのですが、まず、CODのもっとも簡単な形はswitchした後は1回は報酬をあげない、だけどもう一回選んだらあげることにします。Sugrue 04のReference and Notesの11に書いてあることをそのまま理解するとこれをしていることになります。ならば簡単switchしたらもう一回は必ず同じ色を選ぶことにする。問題は、これをするとswitchしたほうがよいかstayしたほうが良いかは2試行先まで見て平均報酬の良いほうを選ぶことです。以前と同様にp_red > p_green の場合に限定して話を進めます。redにいるとき、2試行まで見越してやるとp_red < {1-(1-p_green)^n_red+2}/2の関係が成り立つ最小整数n_redを求めればn_redを連続で選択する回数がわかります。結果はn_red = Max{floor[ (1-2p_red)/(1-p_green) ] -1 , 2}となります。同様にn_greenももとめて、p_red/(p_red + p_green)に対してn_red/(n_red+n_green)を求めれば同じようなグラフが得られます。結果はほとんど同じ、ステップは細かくなりましたが、概要は同じでした.これを使ってモデルは作ってやってみましたが、どうもstay dulation(Fig 2 F)がサルの結果にあわないようです。CODの関係でどうしても2回が多くなる。やはりここまで複雑なことは考えていないかも知れません。
# pooneilp_red + p_green = 1/3、直しておきました。
# mmmmmmrlさん、お疲れさまでした&ありがとうございました。Fig. 2Fでは2回が多いですから、モデルの方がそうならなかったという意味ですね?行動の解析には報酬の各比率のトライアルがが必ずしも均等に含まれているとは限らないので、比率毎に分けて、彼らの行動の結果を見てみたいところです。そのデータがあれば、もう少し妥当なモデル化ができるようになるのではないかと思いますが、これは彼らのみぞ知るデータで、続報(がもしあれば)に出てくるのかもしれないので期待したいところです。