pooneilの脳科学論文コメント

■ 最尤法、MAP法、ベイズ推定についてのまとめ

ずいぶんと昔の話なのだけど、「比率のデータにエラーバーを付けたいんだけど」っていう記事を作ったときに、最尤法でも尤度関数の分布を使ってエラーバー(ベイズ的なcredible interval)を付けることができるよね、というのをやったことがある。そのときどうもしっくりきてなかったことを整理してみる。

最尤法の具体例として(この例自体は今回の話に必須なわけではないが)、二項分布でコインの表裏を $x=\{1,0\}$ で表現するとして、n回のコイン投げデータ $\boldsymbol{X} = \{x_1, x_2,...,x_n\}$ が確率モデル(二項分布)のパラメータ $\theta$ (コインの表が出る確率)の尤度関数 $L(\theta)$ は

$$\begin{eqnarray} L(\theta) &=& p(\boldsymbol{X}|\theta) \\ &=& p(x_1|\theta) * p(x_2|\theta) * ... * p(x_n|\theta) \end{eqnarray}$$

となる。最尤法ではこの尤度関数 $L(\theta)$ の最大値となるパラメータ $\theta$ を推定する。

$$\newcommand{\argmax}{\mathop{\rm arg~max}\limits} \begin{eqnarray} \hat\theta_{ML} &=& \argmax_{\theta}\{p(\boldsymbol{X}|\theta)\} \end{eqnarray}$$

これはベイズの枠組みで言えば、無情報のprior $p(\theta)=c$ を使って計算したposteriorの分布の最大値となるパラメータ $\theta$ を推定することと等価だ。

$$\newcommand{\argmax}{\mathop{\rm arg~max}\limits} \begin{eqnarray} p(\theta|\boldsymbol{X}) &=& p(\boldsymbol{X}|\theta) * p(\theta) / p(\boldsymbol{X})\\ &\propto& p(\boldsymbol{X}|\theta)\\ \theta_{ML} &=& \argmax_{\theta}\{p(\boldsymbol{X}|\theta)\}\\ &=& \argmax_{\theta}\{p(\theta|\boldsymbol{X})\} \end{eqnarray}$$

いっぽうでベイズ推定の場合には、尤度そのものを使うのではなくて、ベイズの定理からposteriorの分布を推定している。

$$\begin{eqnarray} Post(\theta) &=& p(\theta|\boldsymbol{X}) \\ &=& p(\boldsymbol{X}|\theta) * p(\theta) / p(\boldsymbol{X})\\ &\propto& p(\boldsymbol{X},\theta) \end{eqnarray}$$

もしここで点推定したければ、

$$\newcommand{\argmax}{\mathop{\rm arg~max}\limits} \begin{eqnarray} \hat\theta_{MAP} &=& \argmax_{\theta}\{p(\theta|\boldsymbol{X})\} \end{eqnarray}$$

となる。

こうしてみると、posteriorの分布を推論する(inference)ところと、そのあとパラメーター $\theta$ を点推定(estimate)するところを分けて整理できるなと思った。

さっそく作ってみた。

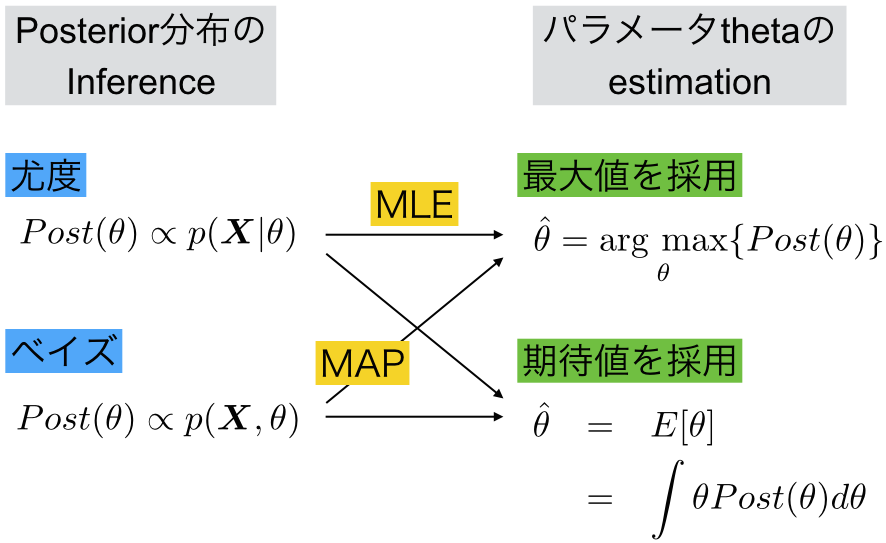
こんなかんじ。ベイズの定理に基づいてposteriorの分布を推論(infer)する方法に対して、priorの情報を使わない尤度を用いた方法がある。どちらもパラメーター $\theta$ の推測(estimate)を行う際には、最大値を採用する方法や期待値を採用する方法がある。

尤度関数の分布を求めた後に最大値を採用する方法が最大尤度法MLE(maximum likelihood estimation)であり、ベイズの公式でjoint probability (=generative model)の分布を求めた後に最大値を採用する方法がMAP法(maximum A posterior)だと。

つまり最大尤度法MLEという言葉を私が気持ち悪いなあと思ったのは、尤度関数を計算するところと、最大値を推定するところとが両方いっぺんに入っているからだということがわかった。「分布関数を計算する尤度推測(likelihood inference)」とそのあとの「最大値を採用する点推定MLE」みたいな言い方をするほうが混乱しなくていいんじゃないの？

なんか、MLEは点推定するけど、ベイズは点推定しないみたいな言い方はmisleadingだと思っていたので。

もちろんこれはベイズ史観であって、MLEを作ったフィッシャーの狙いとは異なるからこんな言い方はしないんだろうけど、そういった歴史的経緯以外にこの捉え方でまずいところってあるんだろうか？

---

でもってじつは本題は、このように整理すると、さらにhidden variable $z$があるときのEMアルゴリズムと変分ベイズを並べることで2*2のマトリクスが作れるよって話だった。でもそこまで図を作る前に息切れしてしまった次第。

---

ところで、当たり前っちゃあ当たり前なんだけど、$p(\theta|\boldsymbol{X})$ も $p(\boldsymbol{X}|\theta)$ も $p(\boldsymbol{X},\theta)$ も $\theta$ の関数であって、同じ一つのグラフの上に書ける。

それは当たり前のことなんだけど、式を字面だけ読んでいると、なんだか $p(\boldsymbol{X}|\theta)$ が $\boldsymbol{X}$ の関数であるような(ぼんやりとした)勘違いをしてしることに気がついた。もちろん、べつに条件付き確率の左右にはどちらがgivenかといったそういう意味があるわけではない。