■ EMアルゴリズムの勉強メモ
自由エネルギー原理を理解するためには機械学習での「変分ベイズ」を理解する必要があって、さらにその手前の段階に「EMアルゴリズム」がある。EMアルゴリズムにおいてもKL divergenceを最小化して下界Lを最大化する過程が出てくる(PRMLの9.4章の図9.11-14)。
この図と式を字面を追っていくことはできるけど、シンプルなモデルでじっさいにグラフを書いて理解できるようにしたい。いちばん簡単な例はなんだろうか? Nature BiotechnologyのPrimerの記事で混合二項分布を使ったいい感じにわかりやすいものを見つけた:Do, C. B., & Batzoglou, S. (2008). What is the expectation maximization algorithm? Nature Biotechnology, 26(8), 897–899.
ここにある事例を使ってmatlabでグラフ書きながら理解してみることにしよう。
潜在変数がない場合 (=>最尤推定)
コインの裏表のデータがある。データXはコインの表の数(列1)と裏の数(列2)を表していて、10回での裏表の数を計算して、それを5回繰り返しす。つまり、データ で、たとえば だと、10回中5回表が出たということ。
X = [...
5 5;
9 1;
8 2;
4 6;
7 3];
じつはコインには二種類、コインAとコインBがあって、それぞれで表が出る確率が違う。この5回でどっちを使ったかのデータがわかっていて、それをZで示している。つまり、データ で、 (A or BでAを使った確率)
Z = [...
0
1
1
0
1];
それではcoin Aおよびcoin Bそれぞれでの表の出る確率 はいくつか?
これは最尤推定で解ける。しかも二項分布の場合は最尤推定を使わなくても、coin Aでは thetaA = 24/30=0.80 , coin Bでは thetaB = 9/20=0.45 という計算だけで済む。
潜在変数がある場合 (=>EMアルゴリズム)
ではもし、いつcoin A, coin Bが出たか(Z)が不明の場合にもcoin Aとcoin Bの表が出る確率を推定することはできるだろうか? つまり入手できるデータはXだけで、Zのほうは入手できない潜在変数という場合でも可能か?というのが問い。
そうすると問題はこのときの尤度
を最大化するような を求めたい、ということになる。
そこで尤度 を最大化する代わりに、
における を最大化する。
これのlogを取ったものの最大化を考える。
(1) 推定する変数 および の初期化
, : コインA, Bそれぞれの表が出る確率
theta_Aest = 0.60;
theta_Best = 0.50;
および
pziAest = [...
0.5;
0.5;
0.5;
0.5;
0.5];
pziBest = 1 - pziAest;
(2) E-step: を計算する
ベイズの公式より
これらが計算できればE-stepでの目的である として
右辺は(2)と(1)から計算できる。
実際にはこれを計算する:
は のときの が起こる尤度だから
px1z1A = binopdf(X(1,1), X(1,1)+X(1,2), theta_Aest)
px1z1A = 0.20066
初期設定より、
よって は以下のように計算できる。
pz1Ax1 = px1z1A .* pziAest(1)
pz1Ax1 = 0.10033
同様にして、 は のときの が起こる尤度だから
px1z1B = binopdf(X(1,2), X(1,1)+X(1,2), theta_Best)
px1z1B = 0.24609
初期設定より、
よって は以下のように計算できる。
pz1Bx1 = px1z1B .* pziBest(1)
pz1Bx1 = 0.12305
まとめると となる。
同様にして について計算すると
pziAxi = ([binopdf(X(:,1), X(:,1)+X(:,2), theta_Aest)]) .* pziAest;
pziBxi = ([binopdf(X(:,2), X(:,1)+X(:,2), theta_Best)]) .* pziBest;
[pziAxi pziBxi]
ans =
0.10033 0.12305
0.020155 0.0048828
0.060466 0.021973
0.055738 0.10254
0.1075 0.058594
を計算するには上で計算した と があればよい。
より
pxi = pziAxi + pziBxi
pxi =
0.22338
0.025038
0.082439
0.15828
0.16609
これが の推定値
pziAest = pziAxi ./ pxi;
pziBest = pziBxi ./ pxi;
[pziAest pziBest]
ans =
0.44915 0.55085
0.80499 0.19501
0.73347 0.26653
0.35216 0.64784
0.64722 0.35278
(3) M-step: の推定
coinAが出る期待値は
X_Aest = X .* pziAest;
X_Best = X .* pziBest;
sumX_Aest = sum(X_Aest,1);
sumX_Best = sum(X_Best,1);
theta_Aest = sumX_Aest(1) / (sumX_Aest(1) + sumX_Aest(2));
theta_Best = sumX_Best(1) / (sumX_Best(1) + sumX_Best(2));
[theta_Aest theta_Best]
ans = 0.71301 0.58134
(4) 収束条件を見てストップするか判断
thetaが収束したかどうかを確認して、E-Mの繰り返しを止めるか決める。
ではE-Mを20回繰り返して、thetaが収束するかどうか見てみることにしよう。
clear all
X = [...
5 5;
9 1;
8 2;
4 6;
7 3];
theta_Aest = 0.60;
theta_Best = 0.50;
pziAest = [...
0.5;
0.5;
0.5;
0.5;
0.5];
pziBest = 1 - pziAest;
theta_est =[theta_Aest theta_Best];
for ii=1:20
pziAxi = ([binopdf(X(:,1), X(:,1)+X(:,2), theta_Aest)]) .* pziAest;
pziBxi = ([binopdf(X(:,2), X(:,1)+X(:,2), theta_Best)]) .* pziBest;
pxi = pziAxi + pziBxi;
pziAest = pziAxi ./ pxi;
pziBest = pziBxi ./ pxi;
X_Aest = X .* pziAest;
X_Best = X .* pziBest;
sumX_Aest = sum(X_Aest,1);
sumX_Best = sum(X_Best,1);
theta_Aest = sumX_Aest(1) / (sumX_Aest(1) + sumX_Aest(2));
theta_Best = sumX_Best(1) / (sumX_Best(1) + sumX_Best(2));
theta_est = [theta_est; theta_Aest theta_Best];
end
figure;
hold on
plot(0:size(theta_est)-1, theta_est(:,1), 'ro-')
plot(0:size(theta_est)-1, theta_est(:,2), 'bo-')
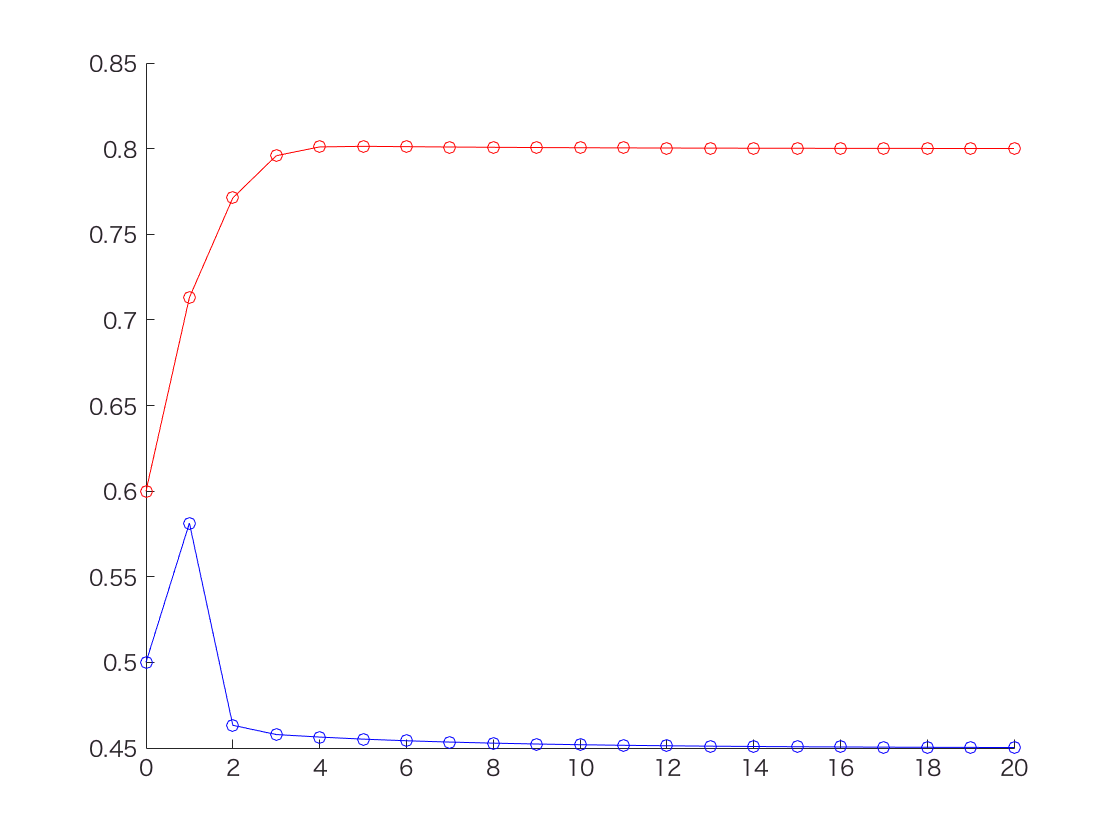
このように、Zが既知での最尤法のときに計算した値(thetaA = 0.80, thetaB = 0.45)と同じ値に収束していることが分かる。
ところでNature BiotechnologyのPrimerの記事では10回繰り返したところでthetaの推定値が thetaA = 0.80, thetaB = 0.52 となってる。たぶんPrimerの記事のほうがなんか間違えてると思う。
