« 「生命の樹」ではなくて「生命の珊瑚」 | 最新のページに戻る
■ 神経活動の力学系的モデルの初歩
神経ネットワークは力学系であり、安定な状態の間を遷移するようなものだ。それを構成する素子である神経細胞も力学系で記述される。神経生理学者として神経細胞の活動は散々見てきたけど、自分でコードを書いてシミュレーションしたことはなかった。(いっときBrianをいじっていたことはあるが。)そういうわけで、Izhikevichの本を参考にして、Matlabのコードを動かして、図を書いてみた。
Izhikevich, E.M. (2007) Dynamical Systems in Neuroscience. MIT Press, Cambridge. https://doi.org/10.7551/mitpress/2526.001.0001
Matlabのコードは吉田のgithubに置いてある。
disclaimer: 式やコードの作成ではGemini 2.0の助けを借りたが、自分の目で確認を取ってある。
[モデルの選択]
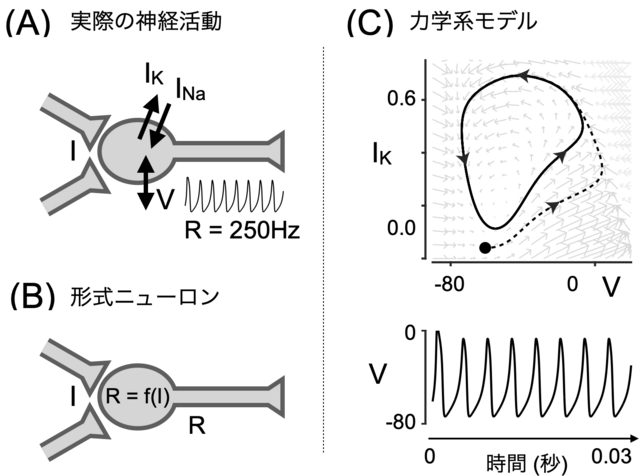
まず図Aにあるように、じっさいの神経活動は、シナプス電位の操作Iと膜を透過するイオンによる電流 $I_{Na}$ および $I_{K}$ によってできる膜電位Vが本体だ。膜電位Vの波形にある活動電位の数を時間あたりのrateとして計算したのが発火頻度Rだ。
図1: 概要
DNNで使われるマカロウ・ピッツの形式ニューロン(図B)では、それを入力Iから出力Rを得る非線形な関数fという形で表現する。
このような簡略化をせず、膜電位Vの時間変動を記述するのが、ホジキン、ハックスレーのモデルだ。それは4つの微分方程式から成り立っている。
これの挙動を扱う大変なので、簡略化が試みられてきた。まずフィッツフュー-南雲モデル(FitzHugh-Nagumo model)では膜電位Vと回復変数Wの二変数の微分方程式を作る。これは回復変数Wの生理学的な意味がわかりにくいので、ここではスキップ。
Izhikevichのsimple modelは膜電位vと回復変数uの二変数の微分方程式を作る。これはじっさいの神経活動の挙動をうまく再現してくれるメリットがある。ただし、単純な微分方程式ではなく、if文的な条件分岐が起こるので、phase plotでの説明には向いてない。
そういうわけで、Izhikevich (2007)の第4章 "Two-Dimensional Systems"で採用されている、ホジキン、ハックスレーのモデルを簡略化して2変数化したモデル(Morris and Lecar 1981)をここでは用いる。それで作ったのが図Cだ。
[スパイキングニューロンモデル (INa,p + IK モデル) の式]
このモデル(INa,p + IKモデル)は、持続性ナトリウム電流 (persistent sodium current, INa,p) と遅延整流カリウム電流 (delayed-rectifier potassium current, IK) を持つニューロンの活動を記述する(Izhikevich (2007) 第4章)。
モデルは、膜電位 ($V$) とカリウムチャネルの活性化変数 ($n$) の2つの変数で記述される。図では簡単のため、$n$ の代わりに $I_{K}$ と表示してある。
$$ \begin{aligned} \frac{dV}{dt} &= f(V, n, I) &\qquad(1')\\ \frac{dn}{dt} &= g(V, n) &\qquad(2')\\ \end{aligned} $$2つの方程式はそれぞれお互いに依存している。入力電流 $I$ はシナプス電流を模したものを表す。この式のとおり、$I$ は$V$ の挙動だけに直接影響を与え、$n$ には直接影響しない。(間接的には、$V$の変動によって影響を与える)
それぞれのパラメーターを明示すると以下の4式になる。はじめの二つが微分方程式で、うしろの二つはそれに影響を与える$V$依存の変数。
$$ \begin{aligned} C \frac{dV}{dt} &= I - g_l(V - E_L) - g_{Na} \cdot m_{\infty}(V) \cdot (V - E_{Na}) - g_K \cdot n \cdot (V - E_K) &\qquad(1)\\ \frac{dn}{dt} &= \frac{n_{\infty}(V) - n}{\tau} &\qquad(2)\\ m_{\infty}(V) &= \frac{1}{1 + \exp{\left(\frac{V_{12m} - V}{k_m}\right)}} &\qquad(3)\\ n_{\infty}(V) &= \frac{1}{1 + \exp{\left(\frac{V_{12n} - V}{k_n}\right)}} &\qquad(4) \end{aligned} $$パラメーターの意味やシミュレーションでのパラメーターの値は、matlabのコードを参照。
[Vector fieldの描画]
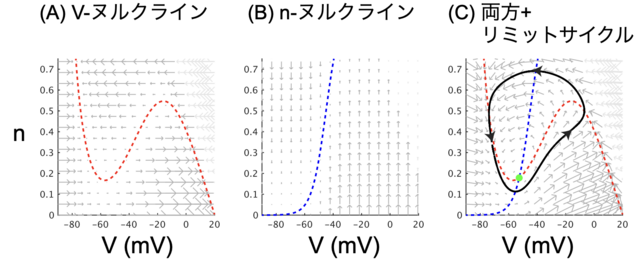
まずはvector fieldを描画する。式(1)と式(2)それぞれからV, nそれぞれについての時間微分をquiver plotで表記したのが図2の(A)と(B)。
図2: vector fieldの可視化
図2AではV(横方向)の傾きの大きさが矢印で表示されている。$dV/dt = 0$ となる点を繋いだV-nullclineが赤点線で重ねてある。(右上の灰色の矢印はそのまま描画すると大きすぎるので、40%に縮小してある。以下の図でも同じ。)
図2Bではn(縦方向)の傾きの大きさが矢印で表示されている。$dn/dt = 0$ となる点を繋いだn-nullclineが青点線で表記してある。
図2AとBを見ただけでこのvector fieldのだいたいの様子がわかる。たとえば(A)では-80mVあたりと10mVくらいに安定な場所があることがわかる。(B)を見ると、Vが-50mVより高いとき、nが大きくなる(=Kイオンが排出される)、Vが-50mVより低いとき、nが小さくなる(=Kイオンの排出が止まる)、という調節がなされていることがわかる。
図2CではV(横方向)の傾きの大きさとn(縦方向)の傾きの大きさを合わせたベクトルが矢印で表示されている。V-nullclineとn-nullclineが交差する場所が緑丸で、ここが安定点になっている。
図2Cは全体的に反時計回りの流れがあることがわかる。黒線はリミットサイクルで、この周りに初期値を置いたとしても、この黒線を反時計回りにぐるぐる回るようになる。
つまりこのvector fieldでは初期値をどこに置くかで2種類の安定性がある。ひとつは緑色の安定点でずっと同じ値であり続けるか、もうひとつは黒色のリミットサイクルを反時計回りにぐるぐる回るか。
[初期値を決めて時間発展の描画]
このようにしてvector fieldを作ることができたら、あとは初期値を設定して、そこから時間発展してゆく様子を計算する。ここではオイラー法を用いている。
(ほかにも修正オイラー法とか、ルンゲ・クッタ法とかもっと正確なものがある。matlabではルンゲ・クッタ法はode45()という関数で実装されている。)
すると、図1C上のような挙動が表示できる。初期値を黒丸のところに置くと、点線を通って、リミットサイクルに取り込まれる。
これを縦軸V、横軸時間でプロットしたものが図1C下。スパイク状の波形が再現できているのがわかる。この波形が活動電位(スパイク)だ。たとえば今の例だと30msの間に8発あるから、だいたい250Hzくらいとなる。
[入力電流Iを変えて挙動を調べてみる]
次にこのモデルで入力電流Iを変えて挙動を調べてみる。
図3: 入力電流Iを変えて挙動を調べてみる
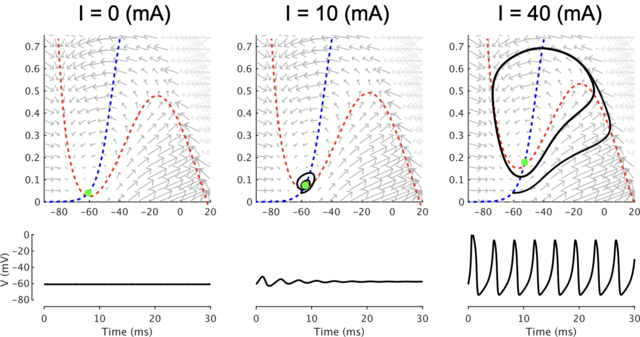
図3は左,中央、右がI=0mV, 10mV, 40mVとそれぞれ変えて、ベクトル場、ヌルクライン、初期値を置いたときの挙動およびVの時間変動を示したものだ。
まずn-ヌルクライン(青線)を比べると、皆同じであることがわかる。上記の式(2')にあるように $dn/dt$ はIに依存しないからだ。一方でV-ヌルクライン(赤色)の方はIが大きくなると上にズレていくのがわかる。入力電流Iはこのように、ベクトル場のV-ヌルクラインを移動させて、矢印の向きを変える働きをしている。
図3の左がI=0mVの場合。初期状態を安定点(緑丸)にしておくと、そのままVの時間変動はなく、一定値になる。
図3の中央がI=10mVの場合。初期状態をI=0mVでの安定点にしておくと、Vは多少振動するが、すぐに安定点(緑丸)に収束する。
図3の右がI=40mVの場合。初期状態をI=0mVでの安定点にしておくと、Vはリミットサイクルに入って、スパイクバーストが続く。
[ネットワークの中での神経活動]
ここでの入力電流Iはシナプス伝達によっておきる電流を模したものであるので、脳内のネットワークに組み込まれている神経細胞においてはこの入力電流Iは揺らいでいる。それゆえにじっさいの個々のニューロンの活動はイレギュラーなものになっている。
それをモデル化しようとするなら、上記のニューロンを繋いでやる必要がある。たとえばIzhikevichのsimple modelでは、1000個のニューロンにランダムな共通入力を入れると脳波的なリズムが出てくるというもの。そうではなくて、あるニューロンの出力を別のニューロンへの入力にして、みたいなことをやりたい。(別ページで扱っているAshbyのhomeostatを、線形ユニットからニューロンモデルで置き換えたものになる。) これは大掛かりになるので、また後日にする。
[まとめ]
神経活動の力学系的モデルについて、生理学的な意味を失わないギリギリのものを使って、説明をしてみた。個々の神経細胞は力学系であって、入力Iの有無によらずに状態stateとして細胞膜電位Vを持っている。
細胞膜電位があまり上がりすぎていればCaイオンが流入して細胞死が起こるし(たとえばALSでの運動ニューロン)、逆にまったく活動がなければまた細胞死が起こり、ネットワークから除去される(こちらは発達期についてはよく研究されている)。このような意味で、神経細胞の活動は細胞のエネルギー代謝などのカップルして、細胞のホメオスタシスに関わっている。
このことはマカロウ・ピッツの形式ニューロンだけ見ていてもわからないことだ。というわけで今回はここまで。
本記事および画像のライセンス: 吉田 正俊 CC BY 4.0
