« 「札幌市時計台、野中郁次郎、北海道博物館」(さうして、このごろ2022年11月版2) | 最新のページに戻る | 「石狩灯台、ぼざろ、例のドレス」(さうして、このごろ2022年11月-12月) »
■ Tonnetzで工作してみた
以前から散発的にやってるtonnetzの考察の続き。
Tonnetzがなんだったかは以前のブログに書いたけど、三和音がトーラス構造(ドーナツ)として描ける、という話だった。
全12音からなるすべてのメジャーコードとマイナーコードが図上のように表記できて、水色矢印、緑矢印、マゼンタ矢印のところで貼り合わせることができる。つまりらせん状の構造をしている。
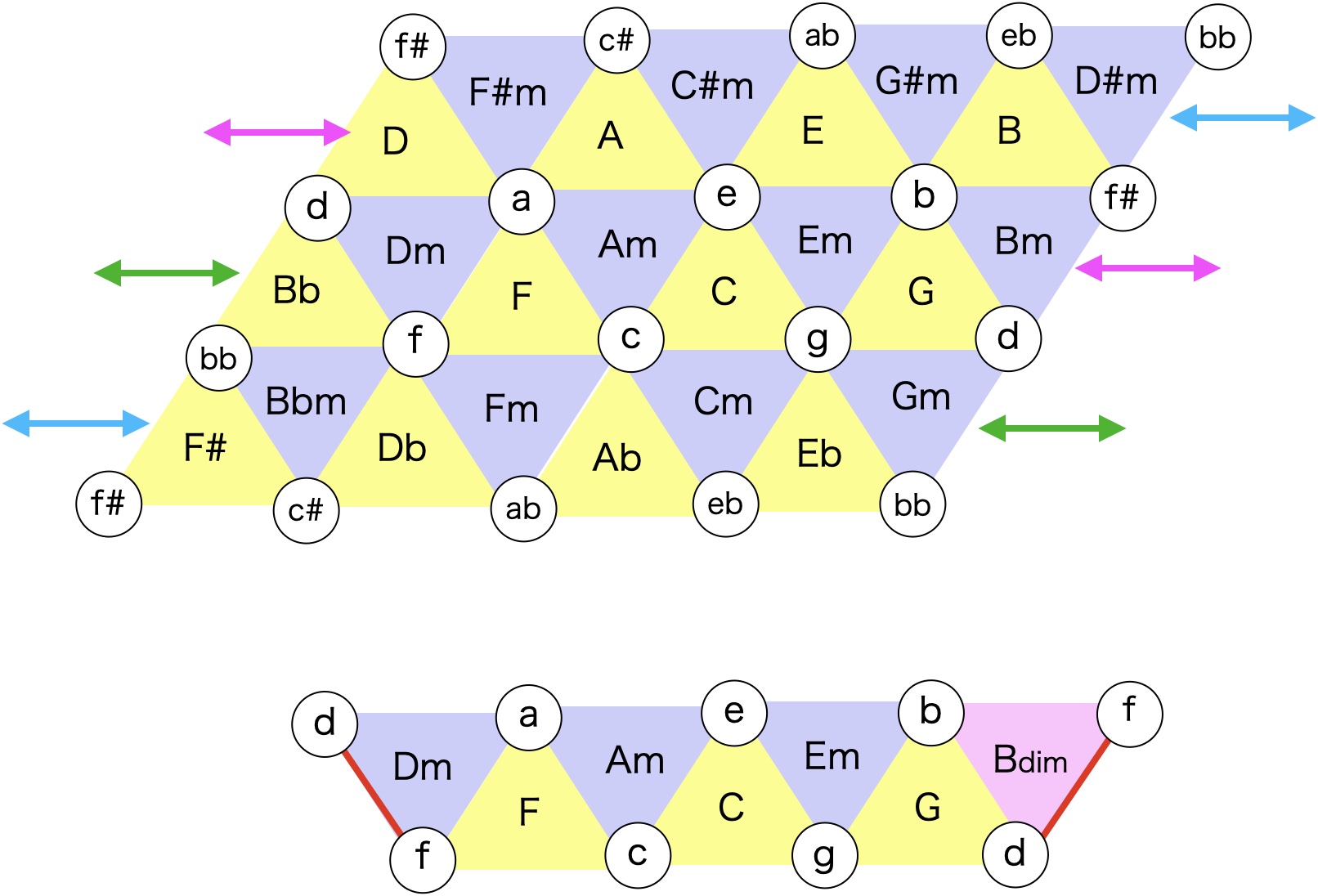
では(たとえば)Cのダイアトニックコードはどこにあるかというと、図上の真ん中の部分を切り出してきて、Bmコードのf#音のところをfに置き換える。するとBdimコードになって、Dmコードと貼り合わせることができる。つまりメビウスの輪になっている、というのが以前の考察だった。
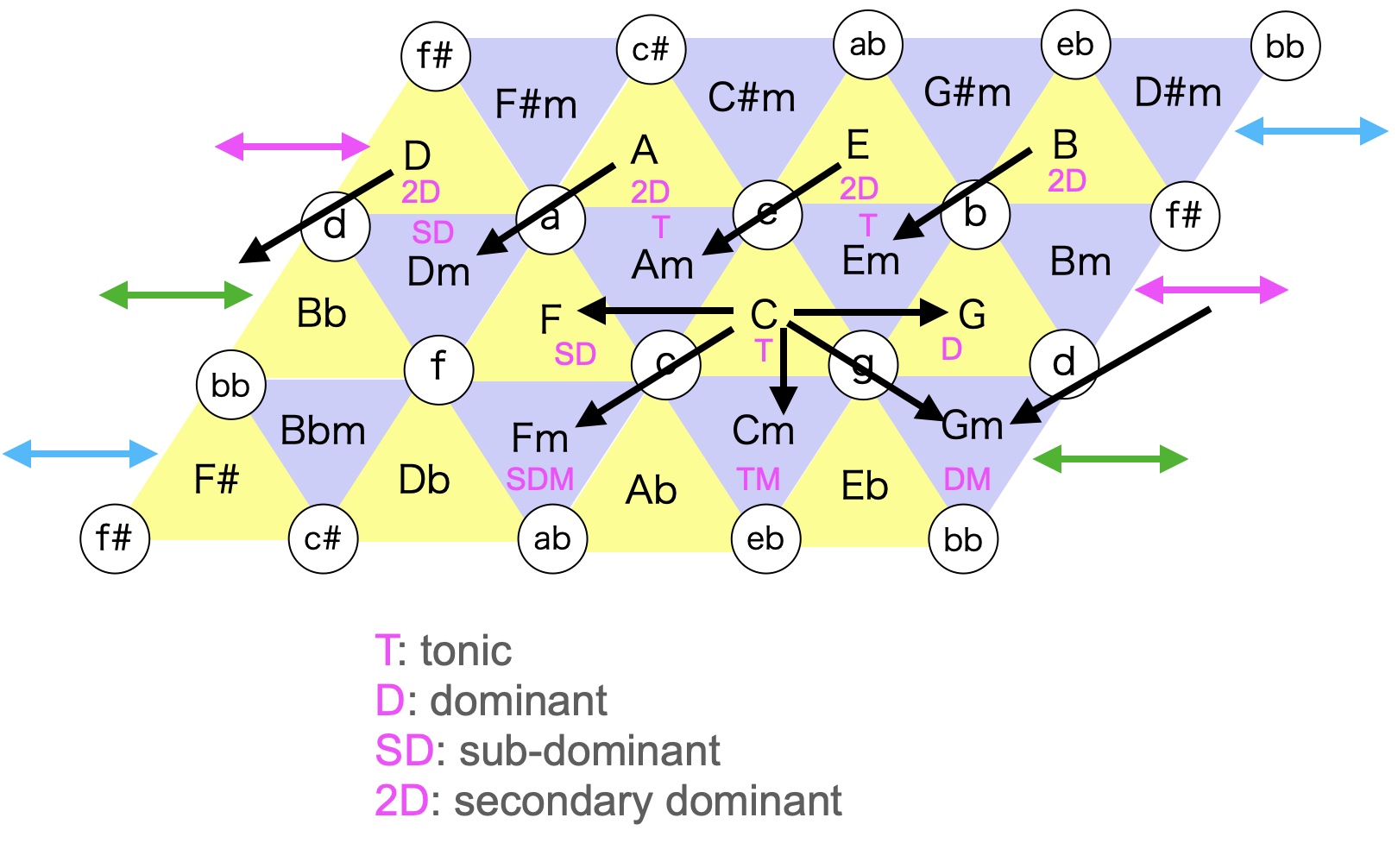
コード間の関係を眺めてみる。Cコードを中心にして、tonicかドミナントか、サブドミナントかを書き込んで(マゼンタ)、さらにドミナント・モーションとかを黒矢印で表記する。
tonicの和音(C,Am,Em)はみんなc音が共通してるんだとか、セカンダリー・ドミナントでのドミナント・モーション(A7->Dm, E7->Am, B7->Em)がぜんぶ平行じゃん、とかいろいろ気づきがある。ジョン・レノン的なC->FmってFmから見ればドミナント・モーションか、とか。
ついでに工作して可視化してみた。
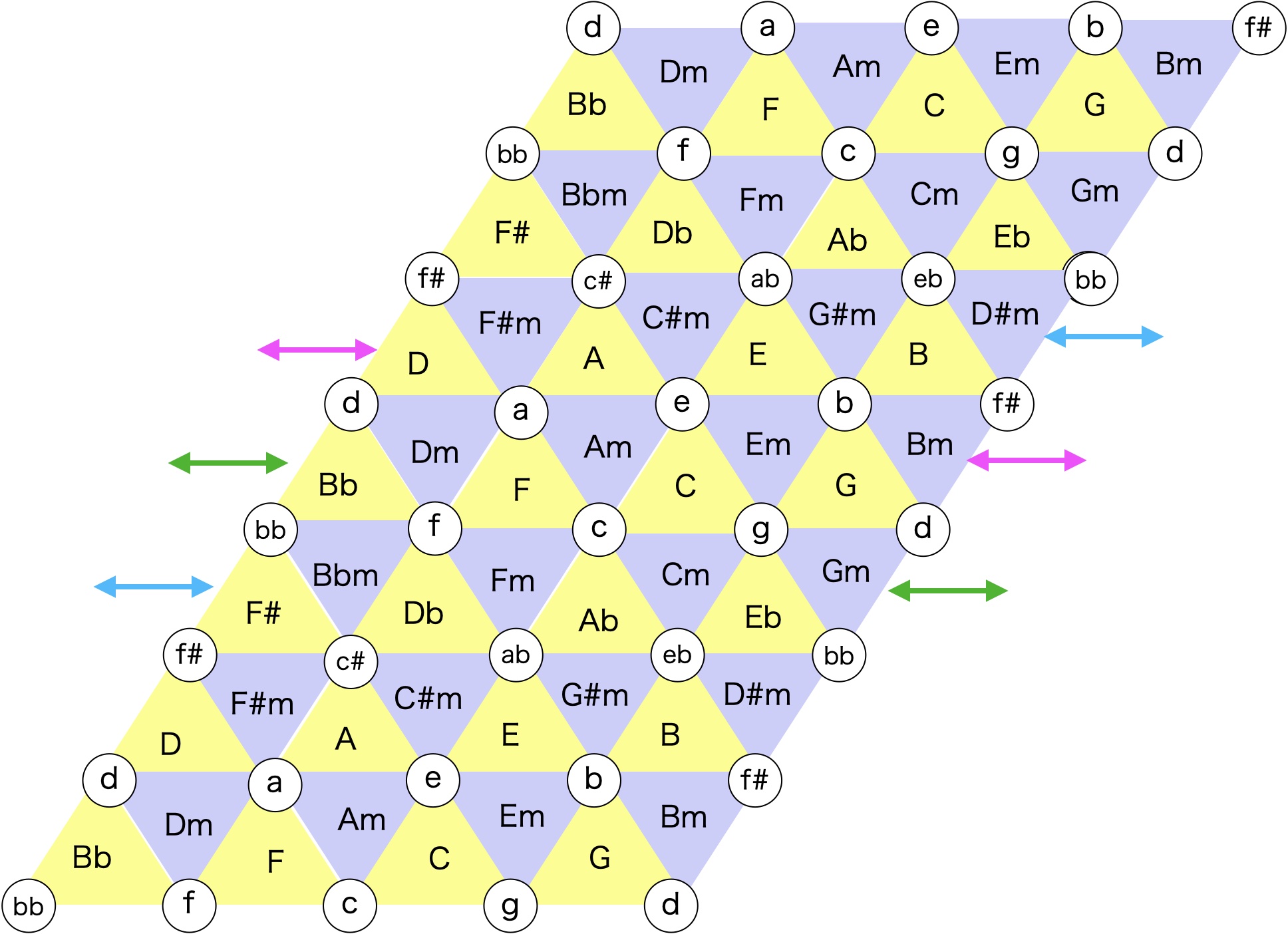
まず2周分作って、貼り合わせてやる。

するとこんなかんじの筒ができて、くるくる回してやることができる。
Cのダイアトニックコードについてもあらためて図示してみる。
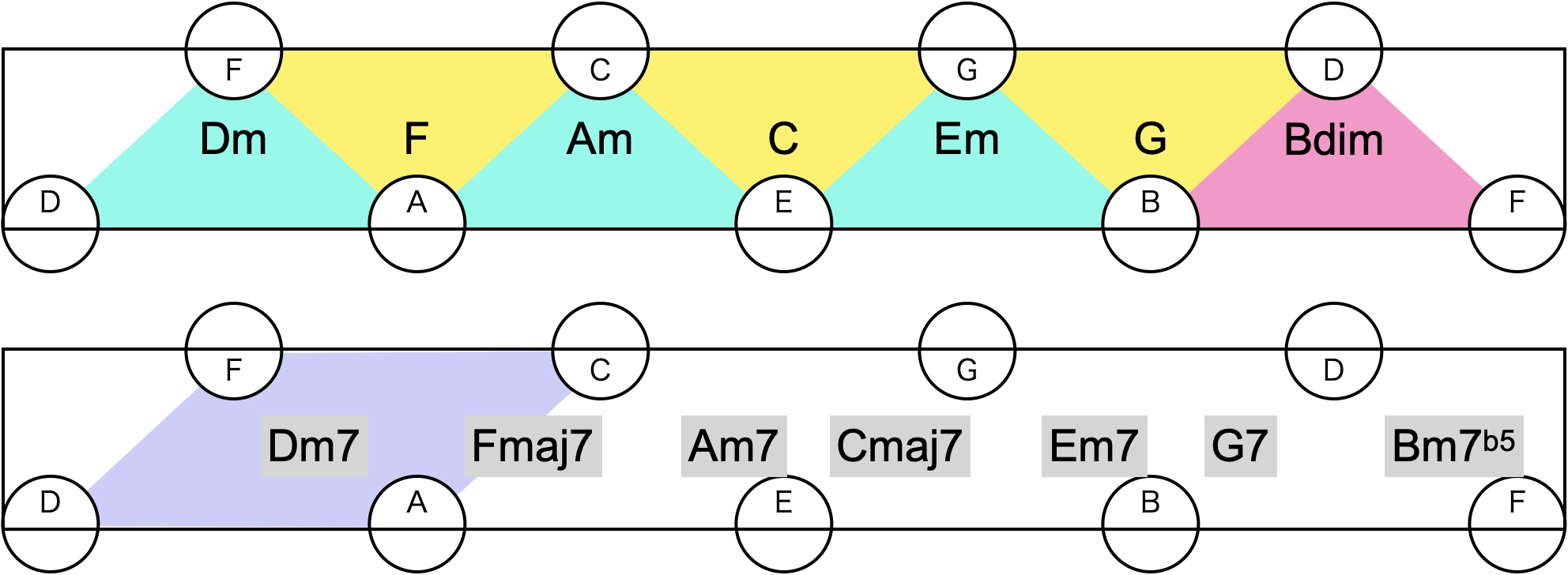
d-f-a音からなるのがDmコードだけど、ここで4和音に拡張してみる。隣り合った4音でできる平行四辺形を考える。たとえばd-f-a-c音はDm7コードになる。
同じようにしてDm7-Fmaj7-Am7-Cmaj7-Em7-G7-Bm7(b5)-Dm7と一周する構造があることがわかる。BdimからBm7b5ができるところはこのメビウスの輪を閉じる意図から明白だけど、GコードがGmaj7でなくてちゃんとG7になるところがいい。当たり前ではあるけれど、G7がほかと比べてちょっと特殊であり、G7->Cmaj7で解決したくなる不安定さがありつつも、Bm7b5ほどは不安定でないというのが納得いく。
これについても工作して可視化してみた。
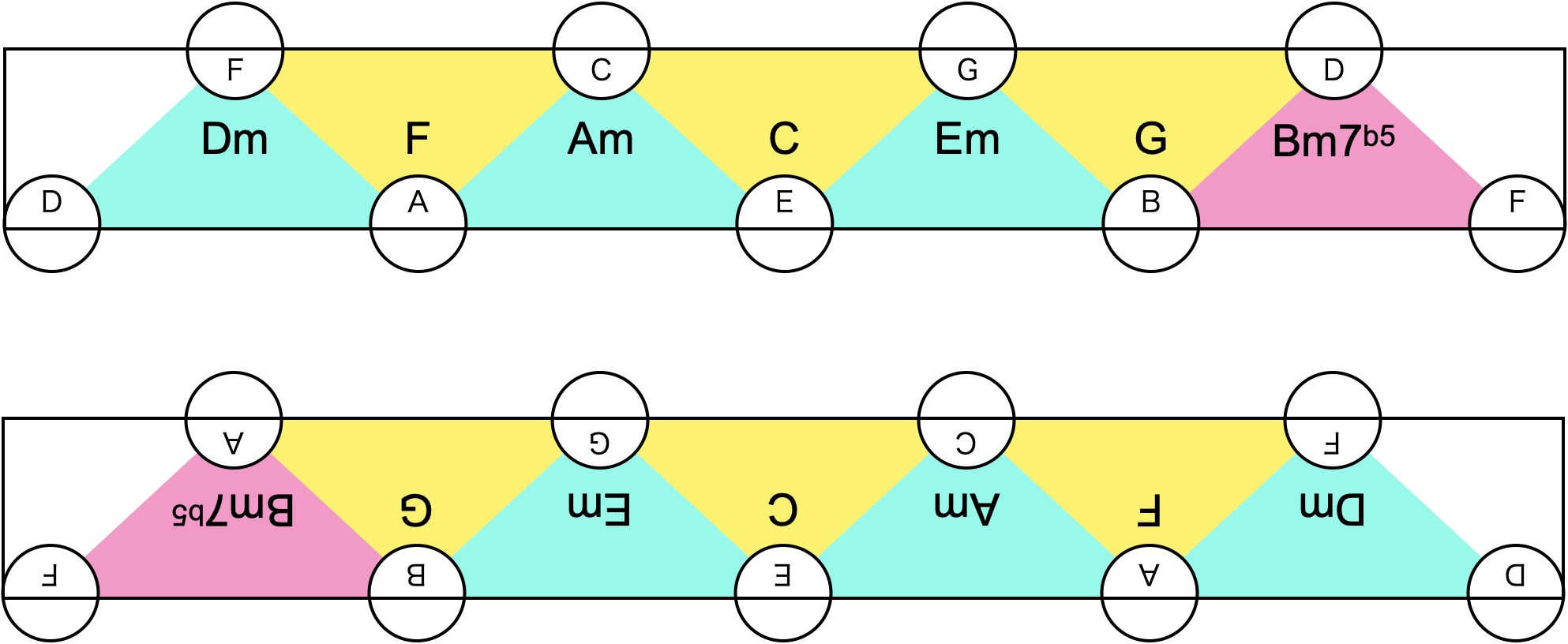
こんなかんじで裏表印刷してやる。

するとたしかにメビウスの輪になってる。たとえばBm7(b5)のa音はb-d-fが作る三角形の真上にあるので、そんなに遠くないことがわかる。
もしかしたら、同じ要領でぜんぶ正四面体を貼り合わせた形にできないか?と考えたけど、以前のジオマグで試した図を見るかぎり、それは無理っぽい。

今回はここまで。