pooneilの脳科学論文コメント

■ BPT_モデル、意志決定の応答潜時モデル、自己組織化臨界現象

さいきんのBPT_分布とかそういう話題(たとえばBPT過程、更新過程メモ、さらに元ネタのpdf)で、応答潜時のdiffusion modelとかで見たことあるようなランダムウォークの図が出てきたので、なるほどこうやって繋がるのかとか思った。

ランダムウォークモデルを使うということは、閾値は一定で、毎度同じ大きさの地震が起こるということを仮定しているわけで、でも実際はそんなことはなくて、いろんな大きさの地震が起こって、その大きさの分布がべき乗則に従うわけだから、生成過程のモデル(process model)の部分をもっと精緻にしたりとかたぶんできるんだろう。

ある震源地で、M1からM9までいろんな大きさの地震が起こっていて、その頻度の分布はべき乗則に従っている(*)んだけれども、たとえばM7以上とかに絞るとけっこう周期があるように見える、というのが実情なのだろう。

(*あとで確認してみたら、これにはグーテンベルク・リヒター則という名前が付いていて、経験則として確立していることを知った。地震発生の頻度を自己組織化臨界現象として捉えるというのは、国内でも元神戸大の伊東敬祐先生のプロジェクトがあったのをwebで見つけたし、けっこう前から複雑系のメイントピックではあるらしい。ともあれ、ここでは意志決定の過程の話をしたい。)

以前に『歴史は「べき乗則」で動く』を読んだときに一時的にかぶれたんだけれども、「科学」の地震の特集の号(たぶん2010年8月号か？)とか読んでみたらぜんぜんそういった複雑系的な話題がなくて拍子抜けした覚えがある。

だから地震の発生頻度の予測にランダムウォークと閾値のモデルを使うというのはかなり簡略化したモデルといえるだろう、みたいな話にして終わるつもりだったのだけれども、逆に考えることができることに気づいた。

つまり、地震だけではなくって、応答潜時に関しても、ランダムウォークで一定の閾値を超えるとイベント発生というのはかなり簡略化したモデルなのであって、実際にはそんな閾値などどこにもない。急速眼球運動(サッカード)の開始コマンドを発生させるニューラルネットワークは試行ごとにいつバーストするかは入力の大きさとは一対一対応には決まっていない。つまり砂山が崩れるタイミングと同じ自己組織化臨界現象となっている。

そう考えると、一定の閾値を超えたらバーストするという心理学的モデルが実際のニューラルネットワークの挙動とずいぶんかけ離れているように見えたものだけれども、もうすこし生理学にできそうな気がしてくる。

もちろん、リアリスティックにすればいいってわけではない。CarpenterのLATERモデルが1/RTが正規分布するというモデルでかなりうまくいったことは、本質をうまいこと突いたことを示している。(LATERモデルは試行ごとにslopeが変わるだけで、試行の中では直線的にevidenceが蓄積する。よってこれはランダムウォークですらない、非常に簡略化されたモデルとなっている。)

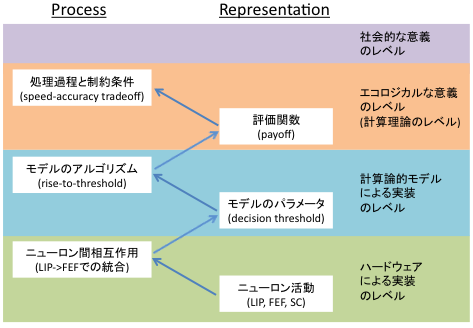
論点はそこではなくて、以前Marrの階層的に応答潜時の計算論モデルを考える、ということをブログに書いたことがある(20100317)けど、あれに関わっている。あのとき書いててぴんとこなかったのは「はたして閾値を作るニューラルネットのprocessとはじつのところいったい何だろう？」もっと簡単に「閾値の実体っていったい何だろう?」ってことだった。

そのときは個々のニューロンのintrinsicな特性とネットワーク的特性、みたいなかんじで自分を納得させていたのだけれど、ここまで考えてくると、そのネットワーク的特性というのを閾値の中に押し込まずに、自己組織化臨界現象がおこるニューラルネットワークの中でとらえる方がよいような気がする。そのうえで改めて、basal gangliaからの入力とかそういったものによる調節をとらえるならば、閾値の上下のような心理的な概念をもっとニューロンの言葉で語ることができるのではないだろうか。

とここまで書いたところで、計算論のひととかだったら当然思いつくことであるような気がした。たぶんそういったアプローチはあるのだろう。だから私としてここで強調したいのはそういったテクニカルなところよりかは、閾値という概念から砂山が崩れるタイミングのような現象への移行だ。

でも意志決定のneural dynamics的なモデルってXiao Xing Wangの(2002それから2006)とかあるなあ。でもNature neuroscience 2006を見直してみたところ、あらかじめthresholdを決めてあるようだ。まだそんなにメジャーなものはないのかもしれない。

ニューロンのバーストをself-organizing criticalityとして見るってのは”Neuronal avalanche”でやってる。neuronal avalancheじたいはスライスだけではなく、最近ではmacaqueのECoGでも見られるらしい(PNAS)。ただしここでやってることは、ECoGから大きい同期発火とおぼしき波形を検出してそれのamplitudeの分布がべき乗則に従っているとかそういう話。

つまり、まず事実レベルとして意志決定の過程での閾値のバーストというのがSOCなのかどうかを検証する段階にあるので、モデルとしてはまだ神経科学内で受容されるほどのところまでは来ていないということなのかも。(物理系のジャーナルとかには出ていてもおかしくない。)

これ以上は論文読んで考えた方がよいことだけど、ふつうにニューラルネットワークのモデルで近接したニューロンどうしてreciprocalに結合した状況で個々のニューロンに閾値があってバーストするようにしてあるだけではSOCにはならない。Criticalであるちょうどよい状態を保つためにはネットワークの相互の結合強度をそのように調整する必要があるし、それがどのくらいロバストなのかとか、そもそもcriticalである必然性があるのかとかいろいろ気になるところはある。

でも、以前言及した"Self-organized criticality occurs in non-conservative neuronal networks during ‘up’ states" Nature Physicsとか見てて、consciousな脳はcritical stateであるってのはなんだかすごく重要であるような気がしてきた。Buzsakiもたぶんなんか言っているよね。

"Rhythms of the brain"見てみた。128ページだ。これはバーストの話ではなくて、脳波の話だけど。なんだか収拾つかなくなってきたので、5章のまとめを貼って終わりとします。

Order in the brain does not emerge from disorder. Instead, transient order emerges from halfway between order and disorder from the territory of complexity. The dynamics in the cerebral cortex constantly alternate between the most complex metastable state and the highly predictable oscillatory state: the dynamic state transitions of the brain are of the complexity-order types. When needed, neuronal networks can shift quickly from a highly complex state to act as predictive coherent units due to the deterministic nature of oscillatory order.

---

(ついったに書いたことを元にして編集して作成した)