« スチュアート・カウフマンの「生命はいかにして複雑系となったか」を読んだ | 最新のページに戻る | 研究関連ツイートまとめ(2020年後半) »
■ 自由エネルギー原理FEP関連メモ
FEPの説明法を見直していた。期待自由エネルギーEFEにいきなり飛ぶのは難易度が高いので、VFE = Uncertainty + Bayesian surpriseの式を使ってきた。これは不正確な方便のつもりだった。でも、行動aからサンプルされる $s$ が一意に決まるときはEFEにせずに、VFEの式でよいと自信を持った。
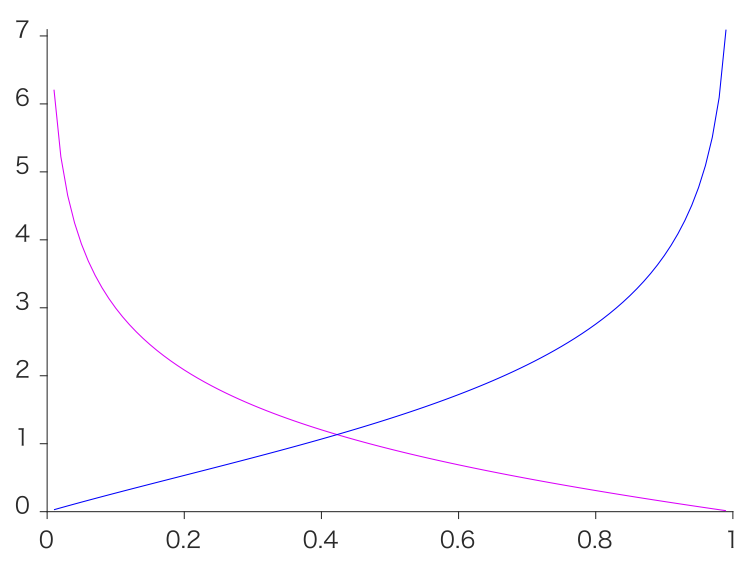
横軸に $p(s=1)$ ($s=1$:左下を見ていて蝶はぼやけてる画像; $s=2$:右上の帳を注視している画像)とおいて、posteriorは固定しておくと、$s=1$ でのUncertaintyはマゼンタ。つまり $p(s=1)<0.42$ で $s=2$ をサンプルする。つまりもし $p(s)$ を自由に動かせるなら、ありふれた $s$ を選ぶ。暗い部屋問題を再現できた。
今のはposterior $p(x|s)$ を固定して、それに $p(s)$ を掛けて生成モデル $p(x,s)$ を作っていた。このように $p(s)$ にアクセスできるなら、暗い部屋問題は起こる。しかし、実際は $p(s)$ は生成モデル $p(x,s)$ を周辺化したモデルエビデンス $p(s|m) = \sum_{x} p_m(x,s)$ なので、agentと環境との関係によって生成モデル $p_m(x,s)$ のほうが先に決まる。(ここでは、生成モデルの形を決めるパラメーターを $m$ と書いている)
そうか、「もっともありふれた刺激 $s$ 」とか言わずに、モデルエビデンス $p(s|m)$ の最大化、と言えばいいのだな。(FEPのような)BIC的なアプローチの代わりにAIC的なアプローチがありうる、って話まで持っていけそう。ぜんぶつなげて話すと、FEPの話ではなくて、ふつうにベイズ統計の授業だなこりゃ。
変分自由エネルギーFはモデルエビデンスの-logの下限(ELBO)なので、自由エネルギー最小化とは、$F_1-F_2 \approx -log(BF_1/BF_2)$ となっていて、ベイズ因子によるモデル選択と同じになる。知覚よりも行動選択の場合だと、$p_{a1}(x,s)とp_{a2}(x,s)$ という2つの生成モデルの比較がしっくりくる。
以前書いた気がするけど、「FEPはなんでも最適化主義ではないか問題」は進化における適応主義論争と形式的には同じで、「理不尽な進化」では適応主義という研究プログラム自体は否定し得ない(最適化というフレームワークで検証をすることの意義)ということでグールドが敗北したことになっているけど、カウフマンが外適応の概念を拾っているのを見て、いやエナクティヴィズム的には再考するお余地があると思った。
「理不尽な進化」も「脳がわかれば心がわかるか」も非常にデネット的なのだけど、グールド敗北で終わらない動機とか、回帰する擬似問題、といったところを残す点がこの2冊では共通してる。
この話への正確なツッコミとしては、「定式化しようと思えば定式化できる(定式化の妥当性、答えの有無に関わらず)」という意味であれば、それは無意味な言明で、それ以降の主張を支える役割を果たしてない。ここで必要な文章は端的に「制約付き最適化って重要だよね」ってことだけだと思う。