« 北海道大学 人間知・脳・AI研究教育センター(CHAIN)の博士研究員の募集を開始しました | 最新のページに戻る | 「ニューラルネットワークを用いた歌声シンセサイザーNEUTRINO」使ってみた »
■ 熱力学の再勉強中。
ここ最近Fristonの自由エネルギー原理FEPについて自分で勉強したり、各地で講演したり、生理研でチュートリアル・ワークショップを開催したり、とさまざまな活動をしてきた。
FEPでは、ベイズの法則による事後分布の計算を変分ベイズでやるために情報理論で言うところの「変分自由エネルギー」を最小化する。(機械学習ではELBO evidence lower boundという呼び名のほうが浸透しているだろう。)
FEPが興味深いのは、環境と相互作用するagentの内部状態がどのように時間発展してゆくかを決定づける変分原理としての役目を果たすかもしれない、という点だ。この点がFEPの特異かつ怪しい部分であって、もしFEPがただの「ベイズの事後分布の簡便な計算法」であるならば自由エネルギー「原理」と銘打つ根拠がない。
先日京大・生命科学の本田直樹さんが企画した国際シンポジウム "COMPUTATIONAL PRINCIPLES IN ACTIVE PERCEPTION AND REINFORCEMENT LEARNING IN THE BRAIN"に参加して、ドイツ ウルム大学のDaniel Braunの連続講演を聞いてきた。
彼は物理的な意味での(ヘルムホルツの)自由エネルギーの最小化を発想の元にして、知覚と行動の統一理論として自由エネルギー最小化を提唱している。Daniel Braunの自由エネルギー原理も発想は違うけど結果としてFristonのFEPと同じものを最小化している。以下の2つの論文が基本理論で、ここから様々な応用をしている。
- Ortega PA, Braun DA (2013) Thermodynamics as a theory of decision-making with information-processing costs. Proc R Soc A 469: 2 LINK
- Genewein T, Leibfried F, Grau-Moya J and Braun DA (2015) Bounded Rationality, Abstraction, and Hierarchical Decision-Making: An Information-Theoretic Optimality Principle. Front. Robot. AI 2:27 LINK
そういうわけでDaniel Braunの論文も読んでいるところで、そのう ちまとめておきたい。それはまた今度。
でもって今回の本題なのだけど、そんなこんなで、そろそろ情報理論での変分自由エネルギー最小化と熱力学、統計力学でのヘルムホルツ自由エネルギーの最小化との対応付け(がそもそもあるのかを含めて)をちゃんと理解しておく必要があるなと思った。
いや、いちおう大学1,2年のときに熱力学、統計力学の講義があって、試験もパスしてはいるのだけど、一夜漬けでぜんぜんダメな成績だった記憶がある。そのあとブルーバックスとか読んではいたのだけど、熱力学を歴史を追って説明するというストーリーで毎度挫折していた。そこでそれとは異なるアプローチで、しかも定評のある「熱力学 ― 現代的な視点から」田崎晴明 培風館 を読むことにした。
この本では、(じつのところ見えない存在である)熱Qの概念からスタートするのではなくて、(計測可能な)仕事Wの概念からスタートして、熱力学を再構成するという話の運びになっている、というところまでは以前調べて知ってた。それでこの三連休を使って1章から7章のヘルムホルツ自由エネルギーの最小化までとにかく読み進めた。
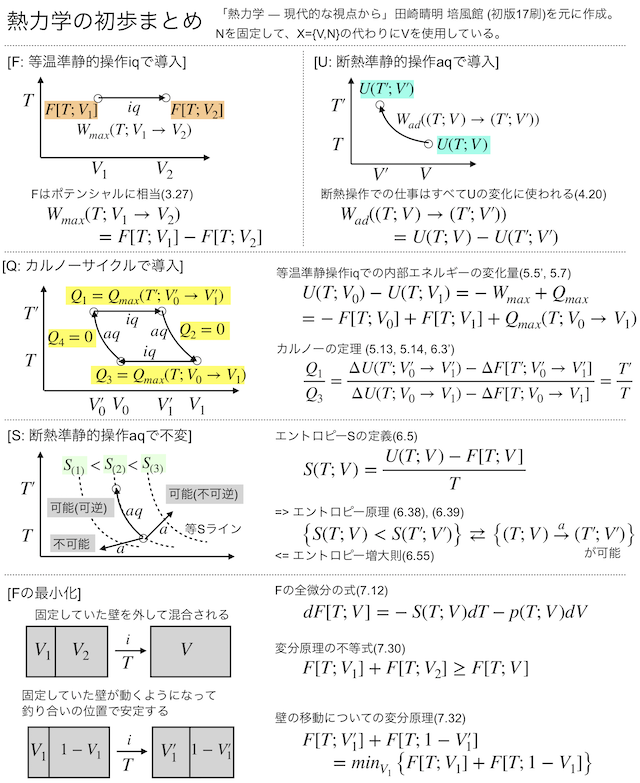
でもって読みっぱなしだと頭に残らないので、こういうときはとったノートをまとめて公開できるように形を整えてみるのがよいだろう(ブログのネタにもなるし)、と考えてまとめノートを作ってみた。まずこちらがA4一枚に収まるように作成したチートシート的なもの。(画像からPDFにリンクしてある。)
もうひとつが9ページ分でまとめた、よりノートらしいノートになってます。こちらはSlideShareにアップしておきました。
この分量を作るだけでもけっこうな時間がかかった。まだ本文を飛ばしながら読んだだけで、繰り返し読んで、例題を解いてゆくことでさらに理解が深まるわけでまだ先は遠い。熱力学自体の勉強としても相転移くらいまでは理解しておきたいし(臨界現象は生物の理論的にも重要そう)。
やってみて再確認できたのは、けっきょくのところ熱力学でのエントロピー、自由エネルギー、といったものは平衡状態でのみ定義可能なものであって(途中の過程自体は平衡であり続ける必要はないけど)、それを生物のような物質の出入りがありながら構造を保ちつづけている非平衡定常状態NESSに単純に当てはめるわけにはいかない。非平衡でのエントロピーをどう定義するか自体が現在でも課題であり、このあたりの進捗をフォローできるように勉強しておく必要があると思った。(FristonのParticular Physics論文でもNESSとマルコフブランケットから話が始まった。)
そして情報理論での変分自由エネルギー最小化との対応付けという意味では本丸は統計力学の方なのだけど、こちらについてはここさいきん渡辺澄夫「ベイズ統計の理論と方法」を読み進めたので、また別の記事を作成できたらと考えている。そちらはまたの機会に。