« 大泉匡史さん「意識の統合情報理論」セミナーまとめ(2/5) | 最新のページに戻る | 大泉匡史さん「意識の統合情報理論」セミナーまとめ(4/5) »
■ 大泉匡史さん「意識の統合情報理論」セミナーまとめ(3/5)
前回のつづき。(全5回分の記事をつなげてPDF化しました。まとめて読むときはこちらを使うことをお勧めします:IIT20161115.pdf)
2. 統合情報量の数学的定式化
ここではまず情報理論の基礎の話からスタートした。内容としてはClinical Neuroscience総説に準拠している模様。
2-1. 相互情報量 (Mutual information)
相互情報量MIは外部の刺激がS=sであることが判明したときにシステムXの不確定性がどのくらい減るかを表現したものであり、KL divergnce (以下式では'D'で表現する)を使って以下のように表現できる。
- MI(X; s) = D( P(X | s) || P(X) )
よって、相互情報量MIとは、Xとsとを両方見ることができる外側からの視点(ideal observer)にとっての情報量であり、extrinsicな情報量であるといえる。
2-2. 内的な情報量 (Intrinsic information)
それでは、あるニューロンAにとっての「内的な」情報量というものを考えるとすればどうすればよいか。それは外界の刺激ではなくて、そのニューロンAへ入力するニューロン群の活動パターンとそのニューロンAが出力を送るニューロン群の活動パターンによって規定されると考えるべきではないか。これはさらにニューロン群でも同様に考えられる。
これをシンプルなモデルで説明するために、図1のようなニューロンA,Bの2個からなるネットワークを考えて、それぞれの発火状態X=1,0(黄色が状態1で白が状態0)が離散的な時間t-1, t, t+1,...でどのように遷移するかの規則(TPM: transition probability matrix)が与えられているものを考える。(Clinical Neuroscience総説の図1,2を参照。)
するとたとえば現在tのネットワークの状態がたとえばAB=10に対して、過去t-1のネットワークの状態AB={00, 01, 10, 11}がそれぞれどのくらいの確率で起こるかということが計算できる(cause repertoire: 大泉さんの表現とは違うが、P(AB(t-1) | AB(t))と書ける)。(上記のTPMがP(AB(t) | AB(t-1))そのものなので、ベイズの定理を使えばよい。) そうしたら現在tの状態AB=10であることが判明したことによってどのくらい過去t-1のネットワークの状態ABの不確定差が減るかということが計算できる。これがintrinsic information。
- ci = D( P(AB(t-1) | AB(t |AB=10)) || P(AB(t-1)) )
(ひとついうべき点としては、このciは現在のstateごとに計算される。全stateで平均しない。(注2))
(吉田コメント) セミナーでは明確に言ってなかったが、これはAB(t-1) と AB(t)の間での相互情報量MIのことだ。つまり今の文脈では「内的」であるためには統合情報量を定義する必要はなくて、外部の刺激ではなく、ニューロンのネットワークが影響をもらい、与えうる因果的なネットワークで定義することが重要であると言える。
これらの説明で出てくる図の矢印は吉田が理解するかぎり、直接的にcausalな影響を及ぼす関係であることを示していて、間接的なものにはこの矢印を付けない。いっぽうで、投射はあるけれどもシナプスの重みは0であるといったように、実際にはcausalな影響がないこともありうる。
2-3. 統合情報量φ (Integrated information)
ではIITでの統合情報量φが相互情報量MIとどう違うかというと、ネットワークのpartitionという操作を用いるところ。現在tの状態AB=10のときのcause repertoireとしてP(AB(t-1) | AB(t |AB=10))が計算できるわけだが、統合情報量ではこれをA-B間の結合を切断(partition)した場合のcause repertoire とを比較して、その距離を計算する。式としてはこういう感じ:
- D( P(AB(t-1) | AB(t |AB=10)) || P_partition(AB(t-1) | AB(t |AB=10)) )
今見ているようなABだけのネットワークであればpartitionはA-Bを切るだけだが、要素数が大きい系ではこのようなpartitionは膨大な個数ある。たとえば要素が12個あったらpartitionは2^11あることになる。このため、IITではMIP (minimum information partition)ということを考える。ここからは説明のため、一時的に4つの要素のネットワークの話に変える。(ちなみに大泉さんのセミナーではここを端折ってたのでMIPの概念、意義の説明がわかりにくくなっていた。)
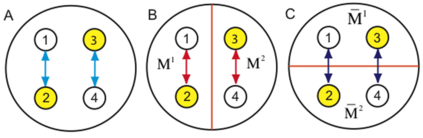
Figure 2 by Balduzzi and Tononi 2008 / CC BY 4.0
図2はIIT2.0論文のFig.3を改変して作成しているが、要素1,2,3,4のネットワークAはじつは1-2および3-4でだけ因果ネットワークが形成されていて、1-2と3-4は独立している。このネットワークを切り分ける方法にはいくつかあるが、BとCの例がここでは示してある。Cではpartitionによって上記距離D>0となるのがわかると思うが、Bのpartitionでは因果ネットワークに変化がないため、上記距離D=0となる。このようにDを最小とするpartitionをIITではMIP (minimum information partition)と呼んでいる。
そしてIITではMIPでのcause repertoireと元のcause repertoireとの距離を計算したものを統合情報量φとして用いる。
- φ = D( P(AB(t-1) | AB(t |AB=10)) || P_MIP(AB(t-1) | AB(t |AB=10)) )
よって、図2Aのネットワークのφ=0となる。つまりこのAというシステムは統合された単位ではないということ。改めて1-2および 3-4という2つのサブシステムでの情報統合量を評価する必要が出てくる。おわかりのとおり、この図はsplit brainを想定していて、exclution postulateが実際にどうimplementされているかの説明になっている。以上のようにして、統合情報量φはinformation, integration, exclusionのpostulateを実装しているといえる。
(吉田コメント) IITはこのMIPという操作によって意識のboundaryがどこであるかという議論に対して一定の答えを出しているといえる。(sensorimotor contingencyとの関連で後述) まずはMIPでφ=0となるような末端を削って意識を引き起こしうるネットワークを限定した上で、そのネットワークでさらにφが最小となるようなpartition (MIP)を見つけて、そのネットワークのφを決めてやる、という2段構えになっているとも言える。前者のboundaryを決めるところにMIPが必要なのは納得がいくけど、後者のシステム固有のlevel of consciousnessを決めるときにMIPが必要だという理屈はそんなに無いように思えるのだけど。ともあれ、IITが想定しているイメージというのは、世界に広がっている因果ネットワークがφ=0で切れたboundaryごとにそれぞれのネットワークが一定の極大値として一意に決まる、そういうもののようだ。
(吉田コメント) IITではこのpartitionという作業を入れないとintegration postulateが満たされないと考えている。このpartitionが必須なのか、というところはIITの根幹に関わる問題で、もしMIで充分なのなら、IITでφを計算する必要はない。現実の脳での測定を元にして、MIではなく、φでないとわからないことがある、ということを示す必要がある。この問題についてはのちほど。
2-4. 統合情報量φと相互情報量MIの関係
これが相互情報量MIやtransfer entropyとどういう数学的関係にあるかということについては「情報幾何論文」で取り扱っている。
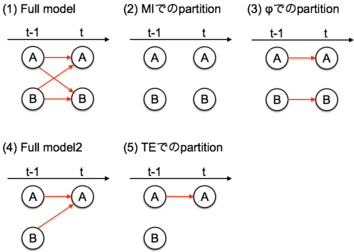
ふたたびABの2つだけのネットワークに戻って考えると、4つの要素{A(t-1), B(t-1), A(t), B(t)}が考えられる(図3-1)。ここでは4つのcausalなlinkを考えることができる(図3-1の赤線)。つまり{A(t-1)->A(t), A(t-1)->B(t), B(t-1)->A(t), B(t-1)->B(t)}
IITのφではこのうち{A(t-1)->B(t), B(t-1)->A(t)}を切った場合、つまりこのリンクが独立である場合(図3-3)とFull model(図3-1)との距離を計算している。いっぽうで相互情報量MIでは4つのcausal linkを全部切って(図3-2)からfull model(図3-1)との距離を計算している。。つまりIITのφに加えて、{A(t-1)->A(t), B(t-1)->B(t)}だけ余計に切っている。よって相互情報量MIは常にIITのφより大きい。
また、さいきん脳データのネットワーク解析でよく使われるようになったtransfer entropy TEはA(t), B(t)それぞれに定義することができる((注3))。たとえばA(t)に対しては3つの要素{A(t-1), B(t-1), A(t)}がある(図3-4; Full model2)。TE(A(t))ではB(t-1)->A(t)を切ったもの(図3-5)とfull model2(図3-4)の距離を計算したものと捉えることができる。よってTE(A)は常にIITのφより大きい。
両方を合わせると、こういう関係が成り立つ。
- TE(A), TE(B) < φ <MI
残念ながらTE(A)+TE(B) < φ <MI は常には成り立たないので、φをTEとMIから推定するというわけにはいかない。(TE(A)+TE(B)はSeth et al 2011で提唱されているcausal densityというやつ)
(吉田コメント) でもこれからわかるのは、現実的な脳のネットワークにおける問題のときにはまずMIとTEを計算しておくとよさそうだということ。また、φを計算するときには常にMIを計算した上で、MIではわからないことがφならわかる、という議論をすることが必要だということもわかる。じっさい、ヒトECoGデータの解析をしたHaun et al bioRxiv 2016ではそういう構造になっている。
次回へつづく。
(注2)相互情報量MIも各刺激S={s1, s2, ...}ごとに計算した情報量iの重み付け平均としても表現することもできるので、この点で統合情報量が相互情報量MIと本質的に変わるわけではない。
- i(X; s) = D( P(X | S=s) || P(X) ) )
- MI(X; s) = Sum( p(S=s) * i(X; s) )
(注3) Gaussianで近似できる系ではTEはgranger causalityと同じになることが知られている。
- / ツイートする
- / 投稿日: 2016年11月27日
- / カテゴリー: [トノーニの意識の統合情報理論]
- / Edit(管理者用)