« モンテカルロ(1) | 最新のページに戻る | The robot said, "this is what it is like to be a bat!" »
■ モンテカルロ(2)
昨日のつづきを貼ります:
昨日のコードを使って、どのくらいのループ回数でどのくらい真の値に収束するか確認してみました。
mloop=1000;sloop=5;loop=10^sloop; data2=zeros(log10(loop),2*mloop); nummat=10.^(1:sloop); tic; for m=1:mloop n=randn(1,1);meanN=n;meanNp=n;ssN=0;ssNp=0;stdN=0; data=[]; for i=2:loop n=randn(1,1); meanN = (meanNp*(i-1)+n)/i; ssN = ssNp + (i-1)*(meanNp^2) -i*(meanN^2) + n^2; stdN = sqrt(ssN/(i-1)); meanNp=meanN;ssNp=ssN; if ~isempty(find(nummat==i)) data=[data;i meanN stdN]; end end data2(:,2*m-1:2*m)=data(:,2:3); end toc; k1=log10(abs(data2(:,1:2:size(data2,2)-1))); k2=log10(abs(1-data2(:,2:2:size(data2,2)))); figure hold on plot(log10(nummat),median(k1'),'ro-') plot(log10(nummat),median(k2'),'bo-')
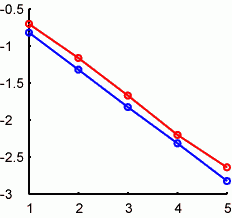
横軸がループの回数(log10(x))。縦軸は計算された値と真の値との差(絶対値)をlog10スケールにて。赤が乱数のmeanによるもので、abs(mean(data))で、青が乱数のsdでabs(1-std(data))です。昨日の計算を10000回繰り返して横軸の各点でのmedianをとっています(非対称分布なのでmean is not = median)。Meanとsdのどちらも直線近似できて、slopeは1/2なのです。これはたぶん差の絶対値だからで、差の二乗を取ればslope=1になったのでしょう。
以上の計算をしなくてもなんかのやり方で導出できるのでしょうけれど(そういうのってなにを読めばわかるのだろうか)、こういうことがわかりました:ループの繰り返し回数を10倍にすると真の値からのズレはsqrt(1/10)=1/3.16だけ小さくなる。
ところでこういうことやってよいか。とくに端数の問題、浮動小数点の問題。全データを用意しておいて、全データで一挙に計算したときとループごとに計算したときで誤差がどのくらいあるか検証してみる。
なんてことを考えて放置したままになっていたのでそのまま貼っておきます。
# ryohei
SE~SD/sqrt(N)になるのと同じ理屈ですね。Nこランダムな数字(が平均)の平均を何回も計算して平均をとると、もちろんが平均。分散はだいたい)^2> = =/Nとなります。(それぞれの事象が独立の場合、クロスタームがすべてゼロになる)。物理実験実習であたりで習った覚えがありますが、多分どの統計の本にも載っているのではないでしょうか。
# ryoheiしまった、< とか>を使うときに注意しなければいけなかったんだっけ。えーと、気を取り直してもう一度、Nこランダムな数字の平均を何回も計算してその平均をとると、もちろん<x>が平均。分散は<(Σxi/N - <x>)^2> = <(Σδx)^2/N^2 >=<δx^2>/Nとなります。(それぞれの事象が独立の場合、クロスタームがすべてゼロになる)。これでやっと書けている感じがします。上のできそこないのコメントは消しといていただけますでしょうか。
# pooneilそっかあ、「SE~SD/sqrt(N)になるのと同じ理屈」、これは明解でした。どうもありがとうございます。meanのmedianを取っているのだけれど、たぶん、数が大きいので、medianをとってもmeanをとってもほとんど変わらなかったのでしょう。