pooneilの脳科学論文コメント

■ 生理研研究会 予習シリーズ：ラットの因果推論と連合学習理論(4)

さて、予習シリーズ前回の続き。今回は数式が多いけど、数式飛ばして日本語だけ読めば話は分かるはず。計算の方は簡単な条件を選んで、なるたけ計算手順省略しないで書いた。

(9/8追記：第一回から最終回までつなげたPDFを作りました。ご利用ください：pdf (11MB))

前回はScience 2006について、実験手順を詳しく追っていって、連合学習理論だけでは説明できない、因果推論に基づいた行動をラットがしているということを確認しました。

そのような行動は認知的理論である、ベイズネットによって説明できる、というわけですが、Science 2006の著者のWaldmann (ゲッティンゲン大学)がまさにこの論文にある実験系をヒトでのcausal knowledgeの研究に使ってきた人でした。

[統計的因果推論・観察・介入]

統計学の世界には「統計的因果推論」という分野がある。ここはまた深い世界だしわたしもよくわかってないので、ここで必要なことだけ書きます。

まずわれわれが「観察」で見ているのは相関であって、因果ではない。そこで「介入」をして何が起こったかを調べる。もしその介入がなかったらどうだったかという「反実仮想」をする。これは現実的には不可能だから、その代わりに介入をしなかった条件のグループを作る。(処置あり/なし * 介入あり/なし の2*2 で二マス分は欠損データになる。) でもって、[介入あり]-[介入なし]で因果関係を検出する、これが統計的因果推論。

このような操作をする際に「介入をする」という概念は統計学にはなかったので、それを「do演算子」というものを使って表現するようにしたのがJudea Pearl。do演算子に関しては後述する。Webで入手できる資料だとここに助けられた。

• 確率と因果を革命的に架橋する：Judea Pearlのdo演算子 ブログへのリンク
• 相関と因果について考える：統計的因果推論、その(不)可能性の中心 (Slideshare資料)

それで、Science 2006の著者のWaldmannはこのような統計的因果推論を、人間の因果推論をモデル化するために使った。ヒト心理実験によって、因果モデルの違い(common-causeかchain-causeか)によって「観察」と「介入」への効果が変わることを示した(Waldmann MR, Hagmayer Y. (2005))。つまり普通の人も、研究者みたいな因果推論をしているんだということ。

このような結果を基にして、それをラットに応用したのがScience 2006だった。

ここでは、ヒト実験(Waldmann MR, Hagmayer Y. (2005))の代わりに、肥満のたとえ話 (Hagmayer et.al., 2007) で説明してみる。

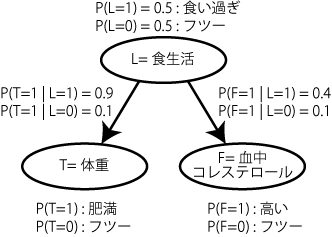
図のようにL,T,Fのcommon causeのモデルがあって、L,T,Fはそれぞれフツーかヤヴァイかの二通り。

ここでは、common-causeについてだけ説明する。まず、Common-causeでの確率は一般的な形で

P(L ,T, F) = P(T | L) * P(F | L) * P(L)

で計算できる。

Common-causeモデルでのobservation条件というのは、上記の一般的な式にT=1を入れたものになる。(Science 2006のテスト試行でトーンが鳴ったのと形式的に同じ。)

P(L, T=1, F) = P(T=1 | L) * P(F | L) * P(L)

一方で、intervention条件はどのように表記できるかというと、前述のPearlのdo演算子というのを使う。do(T=1)と書く。なにが違うかというと、

• 観察: P(L, T=1, F) --- データの中からT=1のものを選ぶ
• 介入: P(L, do(T=1), F) --- Tを1にセットする。

ということ。これは言葉遊びではなくて、実際の計算も変わる。というのも、P(do(T=1) | L) = 1 だから。(Lによらず、T=1にセットしたから。)

P(L, do(T=1), F)
 = P(do(T=1) | L) * P(F | L) * P(L)
 = P(F | L) * P(L)

つまり、intervene条件では、Tはこの因果グラフとは無関係になる。これはなるほど理にかなってる。

では、T=1を見た時にF=1であること(ある人が肥満だった場合に、その人の血中コレステロール量が高い確率)を推定してみよう。これはScience 2006のobservation条件で「Toneが鳴る」から「砂糖水が出る」を推測するのと形式的には同じ。

P(F=1 | T=1)
= P(F=1 | L=1) * P(L=1 | T=1) + P(F=1 | L=0) * P(L=0 | T=1)
= 0.4 * 0.9 + 0.1 * 0.1
= 0.37

P(L=1 | T=1)およびP(L=0 | T=1)はベイズの法則で計算する：
P(L=1 | T=1) = P(T=1 | L=1) * P(L=1) / { P(T=1 | L=1) * P(L=1) + P(T=1 | L=0) * P(L=0) }
P(L=0 | T=1) = P(T=1 | L=0) * P(L=0) / { P(T=1 | L=1) * P(L=1) + P(T=1 | L=0) * P(L=0) }

ではintervene条件で、T=1にセットしたときにF=1である確率を計算してみる。これはつまり重りでも持たせて体重計の目方を因果モデルとはべつのところから操作したときの血中コレステロール量が高い確率だ。

P(F=1 | do(T=1))
= P(F=1 | L=1) * P(L=1 ｜do(T=1)) + P(F=1 | L=0) * P(L=0 ｜do(T=1))
= P(F=1 | L=1) * P(L=1) + P(F=1 | L=0) * P(L=0)
= 0.4 * 0.5 + 0.1 * 0.5
= 0.25

と計算できる。さっきのobservation条件での0.37よりも小さい値になっている、つまり、介入によって、P(F=1)の確率は変わった、つまりわれわれは介入によってFの推定を変えているし、そのことが介入がFを因果的に変えたことを認知している証拠となる。

[ラットの実験に当てはめてみる]

さて、このモデルをラットの実験に当てはめてみよう。じつは実験をデザインする際に、重要な前提条件がある。このようなcommon-causeのベイズネットでモデルするためには、P(T)とP(F)が独立でなくてはいけない。つまり、P(T, F) = P(T) * P(F) でないといけない。(これを違反すると、因果の矢がループしてしまう -- と思ったけど、その場合にはニセの因果を分離できるようなだがどうなんだ？)

一方で、Science 2006、JEPG 2008、IJCP 2009 のすべての実験条件において、L->TとL->Fとは常にべつべつの時間に起こるイベントだったため、独立性の条件を満たしていない。詳しいことは次回説明します。

今回は説明のために、この因果モデルが当てはまるような実験デザインだったとして、Science 2006のような結果が得られたらどのように説明できるか、について書きます。独立性の条件を満たそうとすると、トレーニングは L->TF、つまりライト点灯の後でトーンと砂糖水とが両方同時に提示される条件となります。つまり、

P(F=1 | L=1) = 1
P(T=1 | L=1) = 1
P(F=1, T=1 | L=1) = P(F=1 | L=1) * P(T=1 | L=1) = 1 

ということ。

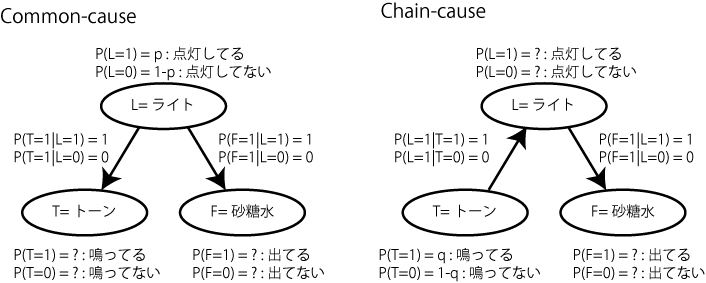
肥満の話との違いは完全に決定論的になっているということ。よって計算はもっとシンプルになる。これでCommon-causeでのobservation条件を計算すると、

P(F=1 | T=1)
= P(F=1 | L=1) * P(L=1 | T=1) + P(F=1 | L=0) * P(L=0 | T=1)
= 1 * 1 + 0 * 0
= 1

Intervene条件を計算すると、

P(F=1 | do(T=1))
= P(F=1 | L=1) * P(L=1 | do(T=1)) + P(F=1 | L=0) * P(L=0 | do(T=1))
= P(F=1 | L=1) * P(L=1) + P(F=1 | L=0) * P(L=0)
= 1 * p + 0 * (1-p)
= p < 1

となる。( P(L=x | do(T=1)) = P(L=x) より。あと、pはテスト期間全体のうちライトの付いている確率なので、1よりも小さい。)

よって、砂糖水が出ている確率を低いものと推測するのでnose poke(CR)が減る、というふうに説明できる。

ではchain-causeのときはどうなるか。まず、chain-causeのときの一般的な関係は、

P(L, T,  F) = P(F | L) * P(L | T) * P(T)

Chain-causeでのObservation条件, intervene条件はそれぞれ

P(L, T=1, F) = P(F | L) * P(L | T=1) * P(T=1)

P(L, do(T=1), F) 
= P(F | L) * P(L | do(T=1)) * P(do(T=1))
= P(F | L) * P(L | T=1)

となる。( P(do(T=1))=1 および P(L | do(T=1)) = P(L | T=1) より。)

Chain-ObservationでF=1(砂糖水が出ているとき)を推測すると、

P(F=1 | T=1)
= P(F=1 | L=1) * P(L=1 | T=1) + P(F=1 | L=0) * P(L=0 | T=1)
= 1 * 1 + 0 * 0
= 1

となる。Chain-InterveneでF=1(砂糖水が出ているとき)を推測すると、

P(F=1 | do(T=1))
= P(F=1 | L=1) * P(L=1 | T=1)  + P(F=1 | L=0) * P(L=0 | T=1)
= 1 * 1 + 0 * 0
= 1

つまり、observation条件とintervene条件とは等しくなる。というわけで実験データを再現できた！

しかしこれは仮想的な実験デザインでの話でした。実際のラットの実験の話については次回。次が最終回。

[参考文献]

• Hagmayer, Y., Sloman, S. A., Lagnado, D. A., & Waldmann, M. R. (2007). Causal reasoning through intervention.(pdf) In A. Gopnik, & L. Schulz (Eds.), Causal learning: Psychology, philosophy, and computation (pp. 86-100). Oxford: Oxford University Press.
• Waldmann MR, Hagmayer Y. (2005) Seeing versus doing: two modes of accessing causal knowledge.(pdf) J Exp Psychol Learn Mem Cogn. 2005 Mar;31(2):216-27.